B1. Number Sense:
Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life.
Learning Situation 1: Combining up to 1000 (Counting)
Total duration: approximately 2 hrs 30 min
| Overall Expectation | Specific Expectations |
|---|---|
| B1. Number Sense Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life. |
B1.1 Read, represent, compose, and decompose whole numbers up to and including 1000, using a variety of tools and strategies, and describe various ways they are used in everyday life. B1.4 Count to 1000, including by 50s, 100s, and 200s, using a variety of tools and strategies. B1.5 Use place value when describing and representing multi-digit numbers in a variety of ways, including with base ten materials. |
Learning Goals
The purpose of this learning situation is to allow the student to:
- count to 1000 in increments of 50, 100 and 200 from a number equal to or less than 1000;
- use the concept of place value to combine units, tens and hundreds.
| Learning Context | Prerequisites |
|---|---|
| Counting activities deepen students' understanding of number patterns and number relationships. By the end of Grade 2, students will have mastered basic counting skills and will be able to count to 200 by 1s and in increments of 2, 5, 10, 20, 25, and 50 from a variety of numbers. In Grade 3, students will learn to count to 1000 by 1s and in increments of 50, 100 and 200 from a variety of numbers. They will also develop their skill with counting backwards in increments of 2, 5, 10, and 100 from a number equal to or less than 1000. The acquisition of strategies for combining by 10s and 100s allows them to handle large numbers more easily. With repeated use of base ten materials, hundreds charts, and number lines, students become more able to discern patterns in counting and to perceive relationships between numbers. | In this learning situation, students will:
|
Mathematical Vocabulary
count, skip counting, ten, hundred, thousand, combine, represent, place value
Materials
Main Activity
- Appendix 3D.1 (Place Value Mat)
- Appendix 3D.2 (Trading up to 500) (2 copies)
- Appendix 3D.3 (Trading up to 1000) (1 copy per team of 2)
- base ten material (2 sets)
- dice (4)
- calculators (if necessary)
Extension
- Appendix 3D.1 (Place Value Mat) (1 copy per student)
- Appendix 3D.5 (Going for 1000) (1 copy per team of 2 or 4)
- different coloured counters (4 per team of 2 or 4)
- dice (1 per team of 2 or 4)
- number cards from 1 to 9 (1 set per team of 2 or 4)
- base ten material (1 set per team of 2 or 4)
Before Learning (Warm-Up)
Duration: approximately 50 minutes
Combining up to 500
Divide the class into 2 teams: A and B.
Provide each team with a copy of Appendices 3D.1 and 3D.2, the base ten material and 2 dice numbered 1 to 6.
Clarify that the object of the game is to be the first team to reach 500, without going over that number, and that each team starts counting from its starting number by 1s or by intervals of 10 or 100.
Ask them to determine the starting number by rolling the two dice. The numbers rolled make up the starting number. For example, if a team rolled a 2 and a 4, they could choose 24 or 42 as their starting number.
Invite a team member to use the base ten material to represent the starting number on the place value mat. For example, if the number chosen is 42, the student could place 4 rods in the tens column and 2 unit cubes in the units column.
Explain the rules of the game:
- A member of Team A rolls a die. The number rolled is the number of times the team can count when it is their turn to play. The team also decides, after each roll of the die, whether to count by 1s or in intervals of 10 or 100. For example, if the team's starting number is 23 and it has rolled 3, the team will count three times from 23 depending on the interval it has chosen: by 1s (24, 25, 26), by 10s (33, 43, 53) or by 100s (123, 223, 323).
- As Team A is counting from their starting point, one student adds base ten material to the place value mat.
- During the game, appropriate trades should be made (for example, 10 ones for a rod or 10 rods for a hundreds flat).
- In each round, the team records its results on the copy of Appendix 3D.2.
Examples
To make three intervals of 100 from 23, students would note the following:

To make four intervals of 10 from 323, students would note the following:
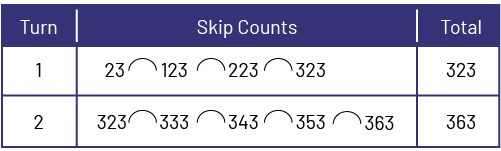
The game continues in this manner, with each team counting from the number indicated on the place value mat. As they approach 500, teams may skip their turn if the number on the die is too high. For example, the team that has reached 496 and rolls 6 would be better off skipping their turn, as they would be over 500.
Ensure that all team members participate in the game by alternating roles each time the die is rolled (for example, 1st student rolls the die, 2nd student adds base ten blocks to the place value mat, 3rd student records the results, 4th student rolls the die, 5th student places the base ten blocks, and so on).
Bring the teams back together when the game is over and ask the following questions:
- What strategies helped you play the game?
- When is it best to count in 1s? 10s? 100s?
- How is the base ten material useful for playing this game?
- What patterns did you notice while counting by 10s? by 100s?
Active Learning (Exploration)
Duration: approximately 50 minutes
Play the Trading up to 1000 game and apply the same rules as the previous game, but teams seek to reach 1000 and "win" with the thousands cube.
Group the students into teams of 4. They will play 2 against 2.
Distribute 2 copies of Appendix 3D.3 (Trading up to 1000) to each team and ask them to record their results.
Circulate during the game. Listen to students and observe the strategies they use.
Ask questions to get them to verbalize their approach, such as:
- Why did you decide to count by 100s this time?
- What would have happened if you had counted by 200s?
- What strategies are you using?
- Why do you need to make a trade now?
Consolidation of Learning
Duration: approximately 50 minutes
Gather students and ask the following questions:
- What was challenging about this game?
- What strategies did you use during the game?
- What did you notice when you counted by 100s? by 200s?
- How did the base ten blocks help you play the game?
- What patterns did you notice when you made the different jumps?
- What patterns have you observed?
Ask students, individually or in pairs, to record their thoughts in their math journals. Suggest a few examples of sentences to complete to facilitate the work.
Examples
- Base ten blocks were useful to me today because…
- During the game, I have…
- If I had to share helpful strategies with a person who plays for the first time, I would say…
- I found the following patterns when skip counting by 100s and by 200s:… (for example, the hundreds always increase by 1 or 2; the tens and units always remain the same)
- When I added 100 to a number like 230 or 340, I noticed that…
- When I added 200 to a number like 364 or 287, I noticed that…
Examples of Success Criteria
The student:
- skip counts by 50s from any starting point.
- skip counts by 100s from any starting point.
- skip counts by 200s from any starting point.
- describes the patterns when the student skip counts by 50s, 100s, and 200s.
- regroups units of ones for tens at the appropriate time.
- regroups units of tens for hundreds at the appropriate time.
- regroups units of hundreds for tens or thousands at the appropriate time.
Extension
Going for 1000
Group the students in pairs or groups of 4.
Give a copy of Appendix 3D.1 to each student.
Distribute a copy of Appendix 3D.5, 4 different coloured counters, 1 die, 1 set of number cards from 1 to 9, and base ten materials to each team.
Ask students to choose a counter and place it on the starting square.
Explain the rules of the game:
- Student A rolls the die or draws a card to determine how many spaces the student can move their counter.
- The student adds up the numbers that the counter has moved to. For example, if the student rolls 5 on the die, starting from the starting square, the student moves the counter 5 squares, namely, 20, 40, 50, 90 and 60. The student adds up the numbers on these five squares, namely, 20 + 40 + 50 + 90 + 60 = 260.
- The student represents the number total on their place value mat (Appendix 3D.1) using the base ten material.
- The other students take turns repeating the same steps.
- The first student who reaches 1000 wins.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 177-184.
Learning Situation 2: Estimation (Quantity)
Total duration: approximately 2 hours
| Overall Expectation | Specific Expectations |
|---|---|
| B1. Number Sense Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life. |
B1.1 Read, represent, compose, and decompose whole numbers up to and including 1000, using a variety of tools and strategies, and describe various ways they are used in everyday life. B1.3 Round whole numbers to the nearest ten or hundred, in various contexts. B1.4 Count to 1000, including by 50s, 100s, and 200s, using a variety of tools and strategies. |
Learning Goals
The purpose of this learning situation is to allow the student to:
- estimate larger and larger numbers;
- develop estimation strategies;
- use estimation to solve real-life problems.
| Learning Context | Prerequisites |
|---|---|
|
Estimation is an important aspect of number sense. In everyday life, whether estimating the value of a few purchases at the grocery store, the mass of an object, or a distance to be travelled, approximate answers are used more frequently than exact answers. For this reason, we must continue to develop the student's concept of quantity and improve the accuracy of their estimations. In Grade 3, students can estimate large quantities, but without benchmarks, their estimations may not be reasonable. A benchmark is a known and understood quantity. Knowing the quantity represented by a benchmark allows one to explore or estimate a larger quantity. For example, if we know that a handful contains about 10 pieces of candy, we can estimate that a jar of candy contains about 6 handfuls, or 60 pieces of candy. It is through repeated activities such as this that the student comes to understand that the use of benchmarks, along with reasoning related to the concept of proportionality, allows for a fair estimation. |
In this learning situation, students will:
|
Mathematical Vocabulary
estimate, estimation, rounding, benchmark, strategy, whole number, likely, more than, less than, close to, greater number, lesser number
Materials
- Appendix 3Q.1 (Estimate How Many) (1 copy per student)
- transparent containers with small objects (1 per team of 3 or 4)
- calculators (if needed)
- large sheet of paper or interactive board
Before Learning (Warm-Up)
Duration: approximately 40 minutes
Many estimation activities require that after estimation, students determine the actual number by counting.
In Grade 3, students are usually no longer willing to estimate an answer since they have to check their solutions anyway. Therefore, they need to be shown the importance of estimating, namely, being able to see if an answer is reasonable or not.
Initiate a discussion to get students thinking about numbers using the following questions:
- What is a large number to you?
Note: Any number that is difficult to estimate can be considered a large number (for example, 50).
- Where have you seen large numbers? What did they represent (for example, car prices at a dealership)?
- What items are found in large quantities (for example, bulk products)
- How can we count those items we find in large quantities?
Record students' ideas on the interactive whiteboard or on a large sheet of paper.
Place several containers with at least 200 small objects (for example, counters, interlocking cubes, bread bag clips, marbles) on a table.
Present the following problem:
I found these containers in a classroom cabinet and would like to know how many objects are in each. I need your help to estimate the amount of objects in each container.
Form teams of 3 or 4 and give each team a container.
Ask students to estimate the number of objects in the container.
Specify that each team should choose a strategy that will help them make the most accurate estimation possible.
Point out that counting all the objects cannot be considered an estimation strategy.
Allow sufficient time for students to have the opportunity to think about the question and discuss the best strategy to use.
Ask teams to record their estimations, apply their strategy, and then count all the objects to see how close the estimated quantity is to the actual quantity.
Observe students at work and check for effective estimation and counting strategies.
Gather the students together for the consolidation. Invite the teams to take turns showing their container of objects and asking the other students to estimate the quantity.
Ask a team member to explain the estimation strategy used (for example, using a benchmark, rounding, combining objects), reveal the estimation, and reveal the actual number of objects in the container.
Check, by a show of hands, how many students were within 5, 10, 20, 30,… of the actual number.
Ask students to identify which estimation strategies seem to work best and explain why.
Discuss the use of benchmarks and how they allow for more accurate estimations.
Emphasize that making an estimation does not mean "determining the exact quantity" but "determining a close approximation".
Active Learning (Exploration)
Duration: approximately 50 minutes
Discuss situations in which an estimation is appropriate:
- When and why do we estimate in everyday life?
- Tell me about a situation where you had to make an estimation.
- What would happen if we underestimated or overestimated the amount of food to buy for the school picnic?
If possible, read books or texts concerning estimation strategies.
Group students into teams of 2 or 3.
Give a copy of Appendix 3Q.1 to each student and have them solve the problems.
Remind students of the importance of benchmarking as a strategy for making accurate estimations.
Consolidation of Learning
Duration: approximately 30 minutes
Invite each team to present a problem and explain the strategy used to solve it.
Write all strategies on the interactive whiteboard or a large piece of paper.
Possible strategies include:
- use of a benchmark;
- use of "friendly" numbers, which are easy to handle (for example, use 20 instead of 23);
- repeated addition or counting;
- rounding to the nearest ten or hundred;
- use of manipulatives;
- use of multiplication.
Ask questions to allow students to reflect on their approach:
- What other estimation strategy could you have used?
- Were your estimations reasonable?
- Would the number 10 (1000, 256) have been an acceptable estimation? Why or why not?
Examples of Success Criteria
The student:
- explains the difference between estimating and counting;
- justifies why their estimation is close to or far from the exact quantity;
- establishes a benchmark and uses it effectively to make their estimation;
- applies efficient estimation strategies;
- justifies the likelihood of an estimation.
Differentiated Instruction
The learning situation can be modified to meet the different needs of the students.
| To Facilitate the Task | To Enrich the Task |
|---|---|
| Begin by having students estimate quantities of less than 100 objects. |
|
