B1.1 Lire, représenter, composer et décomposer les nombres naturels de 0 jusqu’à10 000, à l’aide d’outils et de stratégies appropriés, et décrire de quelles façons ils sont utilisés dans la vie quotidienne.
Habileté : lire les nombres naturels de 0 jusqu’à 10 000
La lecture des nombres permet de les interpréter comme des quantités lorsqu’ils sont exprimés en mots ou en chiffres, ou représentés à l’aide de matériel concret ou de modèles.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Un élève capable de lire ou de nommer un grand nombre n’a pas nécessairement compris ou saisi le sens de cette quantité. Le sens du nombre n’est pas inné.
- Il se développe au cours du cycle primaire à travers des activités de manipulation.
- Il se poursuit au cycle moyen par l’utilisation des connaissances antérieures de l’élève, c’est-à-dire ses connaissances du système de regroupement appliquées aux plus grands nombres.
Le personnel enseignant doit permettre aux élèves de bien comprendre :
- les liens qui existent entre les chiffres qui composent un nombre;
- la valeur des chiffres selon leur position dans le nombre;
- la quantité que les nombres représentent.
Source : L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Le système à base 10
Le système de numération à base dix couramment utilisé aujourd’hui dans bon nombre de pays fait appel à 10 symboles différents, soit les chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. C’est un système dit de position puisqu’une valeur différente est accordée aux symboles selon leur position dans un nombre. Par exemple, le chiffre 2 a une valeur de 2 unités dans le nombre 6 742, alors qu’il a une valeur de 2 000 unités dans le nombre 2 487. La compréhension des relations entre la valeur des chiffres et leur position dans un nombre est essentielle au développement du sens du nombre. Au cycle primaire, les élèves développent une compréhension des relations entre les valeurs de position des unités, des dizaines et des centaines. Cependant, aux cycles moyen et intermédiaire, les élèves ne transposent pas automatiquement cette compréhension aux plus grands nombres. C’est pourquoi le personnel enseignant doit s’assurer de leur faire comprendre que la valeur de n’importe quelle position dans un nombre est toujours 10 fois plus grande que la valeur de la position immédiatement à droite, et 10 fois plus petite que la valeur de la position immédiatement à gauche. Il est aussi important d’examiner les relations de 100 fois ou de 1 000 fois plus grand ou plus petit entre les valeurs de position afin de développer chez les élèves un sens du nombre approfondi, notamment le sens des grands nombres.
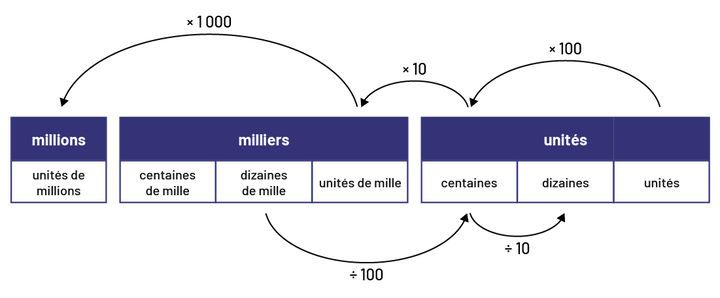 image Grille de position des nombres.De la gauche vers la droite :Millions : qui comprend les unités de millions.Les milliers, qui comprend : les centaines de mille, les dizaines de mille, les unités de mille.Les unités, qui comprennent : les centaines, les dizaines et les unités.Une flèche part de, unités vers centaines, c’est un bond de fois 100.Une flèche part de centaines vers unités de mille, c’est un bond de fois dix.Une flèche part d’unité de mille vers unité de millions c’est un bond de fois mille.Une flèche part de dizaines de mille vers centaines c’est un bond de divisé par 100.Une flèche part de centaines vers dizaines, c’est un bond de divisé par dix.
image Grille de position des nombres.De la gauche vers la droite :Millions : qui comprend les unités de millions.Les milliers, qui comprend : les centaines de mille, les dizaines de mille, les unités de mille.Les unités, qui comprennent : les centaines, les dizaines et les unités.Une flèche part de, unités vers centaines, c’est un bond de fois 100.Une flèche part de centaines vers unités de mille, c’est un bond de fois dix.Une flèche part d’unité de mille vers unité de millions c’est un bond de fois mille.Une flèche part de dizaines de mille vers centaines c’est un bond de divisé par 100.Une flèche part de centaines vers dizaines, c’est un bond de divisé par dix.
Les élèves doivent aussi reconnaître, par exemple, qu’une (1) dizaine de mille représente un regroupement de 100 centaines, un regroupement de 1 000 dizaines ou même un regroupement de 10 000 unités. Ces regroupements permettent de reconnaître des représentations équivalentes de nombres (par exemple, 2 534 est égal à 25 centaines et 34 unités).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 44-45.
Il est important que les élèves comprennent qu’un zéro dans le nombre indique qu’il n’y a pas de groupe à cette valeur de position. Il sert de zéro positionnel et garde les autres chiffres dans leur bonne « position ».
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Le nombre est une représentation abstraite d’un concept très complexe. C’est pourquoi le rapport entre la façon de nommer un nombre et la quantité qu’il représente n’est pas évident pour les élèves. Plusieurs adultes croient à tort que si les élèves savent compter, elles et ils comprennent de facto le sens de chacun de ces nombres. Pourtant, un ou une élève peut bien être en mesure de lire et de nommer un nombre, par exemple, cinquante-huit mille, sans vraiment avoir un sens de la quantité qu’il exprime.
Le personnel enseignant doit les aider à établir des liens entre le système de numération à base dix et la façon de nommer et d’écrire les nombres.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 65.
Une stratégie favorisant l’association du nombre à la quantité qu’il représente consiste à le nommer en mettant l’accent sur la valeur de position de chacun des chiffres qui le composent (par exemple, au lieu de lire le nombre 62 098 en disant soixante-deux mille quatre-vingt-dix-huit, les élèves peuvent dire 6 dizaines de mille, 2 unités de mille, 9 dizaines et 8 unités) ou sur certains regroupements (par exemple, 62 unités de mille et 98 unités).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 70.
La représentation mentale
La représentation mentale d’une quantité est l’image, élaborée par la pensée, qu’on se fait d’un nombre. Lorsque les élèves entendent et lisent un nombre, elles et ils doivent « voir » la quantité que représente ce nombre et en comprendre le « combien ».
Il est donc important que les élèves aient des représentations mentales de différents nombres dans différents contextes. Prenons, par exemple, le nombre 2 000, qu’on peut se représenter mentalement par 2 grilles de 1 000 ou 20 grilles de 100, par le nombre de sièges que l’on trouve dans un amphithéâtre, par 40 autobus scolaires transportant 50 élèves, etc.
Il est important que les élèves se fassent des représentations mentales variées des nombres. Ces visualisations peuvent représenter simplement des quantités. Par exemple, le « combien » de 10 000 peut engendrer une représentation mentale de 10 grilles de 1 000. Cependant, la présence d’unités dans une situation peut favoriser une représentation mentale différente et plus précise, laquelle serait en relation avec une situation donnée. Par exemple, les élèves peuvent visualiser que 5 000 personnes, ce sont 10 écoles comportant 500 élèves.
De plus, si le contexte le suggère, les élèves peuvent porter un regard critique sur la quantité (par exemple, déterminer si celle-ci est « beaucoup » ou « peu »). La représentation mentale sera alors teintée par le contexte. Par exemple, la représentation mentale de 100 personnes à une fête familiale n’est pas la même que celle de 100 personnes dans une foule à l’occasion d’un match de hockey. Les diverses représentations mentales sont toutes valables; elles dépendent essentiellement du contexte de la situation et du sens du nombre qu’ont les élèves. La représentation mentale demeure personnelle, mais l’aisance avec laquelle un individu peut visualiser les nombres est un indicateur de son sens du nombre.
Afin de développer des représentations mentales, les élèves utilisent différentes stratégies qui répondent à des situations et à des besoins variés. Avec de très petits nombres, il est possible pour eux d’utiliser la reconnaissance globale, c’est-à-dire quantifier les éléments d’un petit ensemble d’objets donné sans en dénombrer chacun des éléments. Pour reconnaître de plus grandes quantités, les élèves auront recours à d’autres stratégies. Par exemple, il peut être laborieux de dénombrer chaque pois d’un paquet de petits pois; le regroupement peut alors être utilisé.

Ainsi, après en avoir dénombré 10, elles et ils peuvent constater qu’il y a 3 ensembles égaux pour un total de 30 pois. Dans ce cas, la stratégie du dénombrement (10) est combinée avec la stratégie de reconnaissance globale (3 ensembles). En cheminant, les élèves utilisent de plus en plus le regroupement pour comprendre la quantité. Ainsi, les élèves se créeront des représentations mentales en visualisant des regroupements égaux, par exemple, en visualisant 30 comme 3 ensembles de 10 pois.
La représentation mentale de grands nombres peut difficilement se faire en reconnaissant individuellement les éléments. Elle pourra cependant être créée en utilisant des repères qui seront mis en rapport avec une grande quantité (par exemple, reconnaître que 6 000 personnes c’est environ trois fois le nombre de spectateurs dans un amphithéâtre ayant 2 000 sièges.).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 29-31.
Repères
De façon générale, un repère est une marque, un jalon, un élément de référence. Dans le cadre du développement du sens du nombre, l’utilisation de repères favorise la représentation mentale et, de ce fait, facilite la compréhension du nombre et de la notion du « combien ». Les repères, sans lesquels il est difficile de comprendre la quantité, sont des nombres ou des quantités aisément représentables mentalement puisque ceux-ci ont déjà été vus et manipulés. Les élèves auront de la difficulté à comprendre la quantité si des repères ne sont pas utilisés. Par exemple, en lisant un extrait d’un livre de records, les élèves voient des nombres associés à du texte. Les élèves saisissent que les quantités mentionnées sont d’un ordre de grandeur impressionnant, mais souvent n’ont pas le sens véritable de ces quantités, puisqu’elles et ils n’établissent pas de liens entre ces nombres et des repères significatifs pour eux. Tel est le cas d’une ou d’un élève qui lit l’extrait suivant :
 image Encadré :Le nouveau-né le plus lourd.Le 19 janvier 1879, la canadienne Anna Bates accoucha chez elle d’un garçon qui pesait dix kilos virgule 8 et mesurait 76 centimètres. (Parenthèse ouvrante) Guinness World Records, 2005, page 22 (parenthèse fermante).
image Encadré :Le nouveau-né le plus lourd.Le 19 janvier 1879, la canadienne Anna Bates accoucha chez elle d’un garçon qui pesait dix kilos virgule 8 et mesurait 76 centimètres. (Parenthèse ouvrante) Guinness World Records, 2005, page 22 (parenthèse fermante).
L’élève réagit et trouve ce fait extraordinaire, cependant elle ou il n’a pas mis la quantité 10,8 kg en relation avec des repères. Ce fait est extraordinaire, car c’est un « record », mais l’élève ne saisit pas qu’il s’agit probablement de plus du double de son poids à sa naissance ou ce que représente réellement un bébé de 10,8 kg.
À la suite d’expériences (par exemple, étude de la monnaie, compte par intervalles de 200, 250, 500 et 1 000) et d’apprentissages (par exemple, intériorisation de relations telles que \(4\; \times \;250\; = \;1\;000,\;1\;000\; = \;2\; \times \;500,\;5\; \times \;200\; = \;1\;000\)), les nombres tels que 200, 250, 500 ou 1 000 peuvent devenir des repères. Ainsi, 3 200 peut être compris comme 2 500 plus 700 ou 2 500 plus 500 plus 200, et le nombre 8 000 peut être rapidement associé à 4 groupes de 2 000.
Bien que la majorité des élèves qui arrivent en 4e année sachent lire et écrire symboliquement les nombres jusqu’à 1 000, elles et ils ne comprennent pas nécessairement la quantité représentée par ces grands nombres. C’est en créant des repères et en visualisant des regroupements que les élèves développeront une meilleure compréhension du concept de quantité représentée par de grands nombres.
Les repères sont particulièrement utiles pour comprendre les grands nombres, puisqu’il est généralement impossible de reconnaître globalement ces quantités ou de les saisir par le dénombrement. Les élèves doivent alors s’en faire une idée en la comparant avec un repère. Par exemple, l’école vient de recevoir 10 000 feuilles pour des photocopies. Le concierge devrait-il demander de l’aide pour les transporter? Afin que les élèves puissent vraiment comprendre la situation et la quantité en jeu, elles et ils doivent se créer une image mentale de ce que 10 000 feuilles peuvent représenter. En utilisant un paquet de 500 feuilles comme repère, les élèves peuvent imaginer cette quantité et appliquer la relation de proportionnalité pour déduire que 2 paquets contiennent 1 000 feuilles. Donc, 10 000 feuilles, ce sera 10 fois plus de paquets, soit 20 paquets de feuilles. On peut même reconnaître que 20 paquets équivalent à 2 boîtes de papier. La représentation mentale de l’espace qu’occupent ces 10 000 feuilles devient alors possible. Et la réponse à la question de départ, à savoir si le concierge devrait demander de l’aide pour transporter les feuilles, peut alors être débattue en toute connaissance de cause.
Les élèves doivent s’approprier des repères afin d’y avoir plus facilement recours selon le contexte et les nombres traités. Il n’existe pas de liste de repères. Ceux-ci sont personnels et proviennent des expériences vécues par tout un chacun. Toutefois, les situations de la vie courante fournissent au personnel enseignant suffisamment d’occasions d’attirer l’attention de leurs élèves sur la quantité et la création de repères.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 33-35.
Habileté : représenter les nombres naturels de 0 jusqu’à 10 000
Les élèves doivent apprendre à représenter les nombres de diverses façons et à les reconnaître sous leurs multiples représentations. Ces habiletés les aident à établir des liens entre un nombre, sa représentation et la quantité qu’il représente. Il est donc essentiel que les élèves soient exposés à différentes représentations des nombres. Il importe aussi que les élèves soient exposés à divers contextes qui les mènent à représenter un nombre selon chacun des modes de représentation illustrés dans le schéma suivant ainsi qu’à passer d’un mode de représentation à un autre.
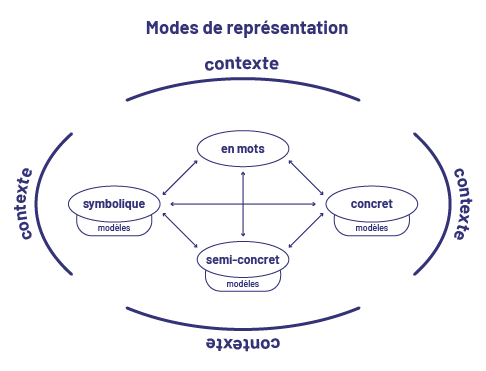
Le personnel enseignant doit être conscient de l’ordre dans lequel il exploite ces quatre modes de représentation avec les élèves. Baroody et Coslick (1998, p. 3-8 à 3-16) suggèrent de présenter un nouveau concept dans un contexte réel et significatif pour que les élèves puissent d’abord se créer des représentations à l’aide de mots, puis des représentations concrètes et semi-concrètes. Ce n’est que lorsque les élèves auront développé une certaine compréhension du concept qu’elles et ils pourront passer à sa représentation symbolique. Les élèves doivent être en mesure d’établir des liens entre les représentations et de passer aisément d’une représentation à une autre.
Représentations à l’aide de mots
En 4e année, les élèves apprennent à lire et à écrire en lettres les nombres jusqu’à 10 000. Il ne faut pas sous-estimer les défis que pose l’écriture des nombres en lettres. Pour aider les élèves à surmonter ces défis, le personnel enseignant devrait inclure les nombres au mur de mots et construire avec eux des référentiels pour résumer les règles d’accord en nombre de vingt, cent et mille.
Représentations concrètes
L’utilisation de matériels de manipulation (par exemple, jetons, matériel de base dix) pour représenter des nombres aide les élèves à développer le sens du nombre.

Une mise en garde s’impose lorsqu’il est question d’utiliser le matériel de manipulation. Il importe de reconnaître que ce matériel permet de représenter un concept mathématique, ce n’est pas le concept lui-même; par exemple, la planchette n’est pas une centaine, mais elle représente une centaine de petits cubes.
Le danger est que les élèves utilisent le matériel de façon mécanique sans faire les liens avec les concepts mathématiques sous-jacents. C’est pourquoi le personnel scolaire doit s’assurer qu’il y a vraiment apprentissage et non pas seulement une utilisation aveugle du modèle. Par exemple, il est facile pour les élèves de remplir les espaces dans la phrase sous l’image en regardant le tapis de valeur de position.
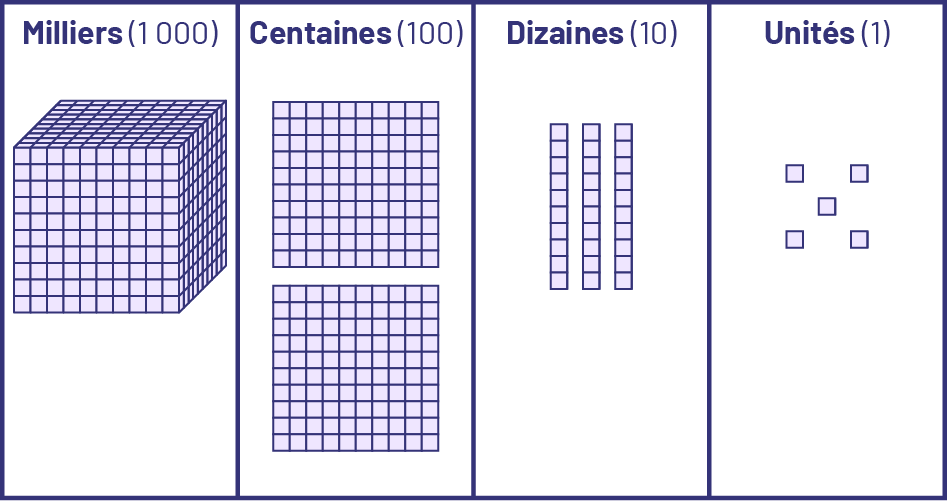
La représentation est ____unité(s) de mille, ____centaine(s),___dizaine(s) et ____unité(s)
Mais est-ce que les élèves comprennent qu’il y a aussi mille deux cent trente-cinq petits cubes ou unités sur le tapis et que c’est une des réalités qui sont représentées par le nombre 1 235? Il est important de demander aux élèves d’expliquer de différentes façons ce qui est représenté. Par exemple, 1 235, c’est aussi 12 centaines d’unités et 35 unités ou encore 123 dizaines d’unités et 5 unités.
Une autre façon de vérifier la compréhension est, par exemple, de demander aux élèves combien il y a de centaines dans 1 235. Plusieurs élèves auront tendance à dire qu’il y en a 2. Il importe alors de préciser que le chiffre dans la position des centaines est un « 2 », mais que le nombre 1 235 est composé de 12 centaines (12 regroupements de 100 unités = 1 200). On peut « voir » ces 12 centaines en décomposant le gros cube en 10 planchettes que l’on ajoute aux 2 planchettes qui sont dans la colonne des centaines.
En utilisant le tapis de valeur de position, on remarque que même si les nombres s’écrivent de gauche à droite, ils sont formés de droite à gauche : les unités regroupées forment les dizaines, les dizaines regroupées forment les centaines, et ainsi de suite. Mais, une fois le dénombrement terminé, on écrit le nombre en partant de la gauche.

Le choix du matériel mis à la disposition des élèves peut aussi faire une différence dans le niveau de compréhension des concepts. On trouve sur le marché une variété de matériels pour représenter les nombres : billes, cubes emboîtables ou tout autre objet pouvant être utilisé pour dénombrer. Certains de ces matériels représentent clairement et concrètement la relation de grandeur entre les unités, les dizaines, les centaines… (par exemple, le matériel de base dix utilisé dans les photos précédentes). Cependant, avec d’autres matériels, cette relation est représentée de façon plus abstraite. Par exemple, sur un abaque ou un « compteur de points », le groupement est représenté en fonction de la position du chiffre de gauche à droite, comme dans l’écriture symbolique des nombres.

En exposant les élèves à une variété de matériels de manipulation, le personnel enseignant peut les aider à développer une meilleure compréhension des nombres.
Représentations semi-concrètes
Les élèves peuvent aussi représenter les nombres avec du matériel semi-concret (par exemple, illustration, grille de nombres, droite numérique).
Illustration : Un nombre peut être représenté par des dessins de façon à illustrer certains regroupements. Par exemple, le nombre 376 peut être illustré par regroupements de 50 comme suit :
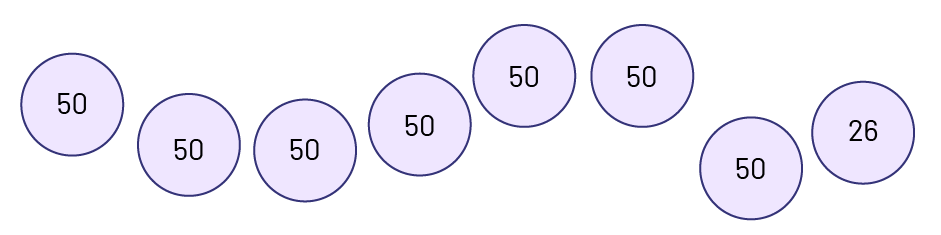
Son illustration peut aussi être en lien avec le matériel de manipulation.

Grille de nombres : La grille de nombres jusqu’à 100 est très utilisée au cycle primaire. Quoique plus difficile à manipuler, une grille de 1 000 peut aider les élèves au cycle moyen à mieux comprendre les nombres en permettant de les comparer et de faire ressortir les relations entre eux.
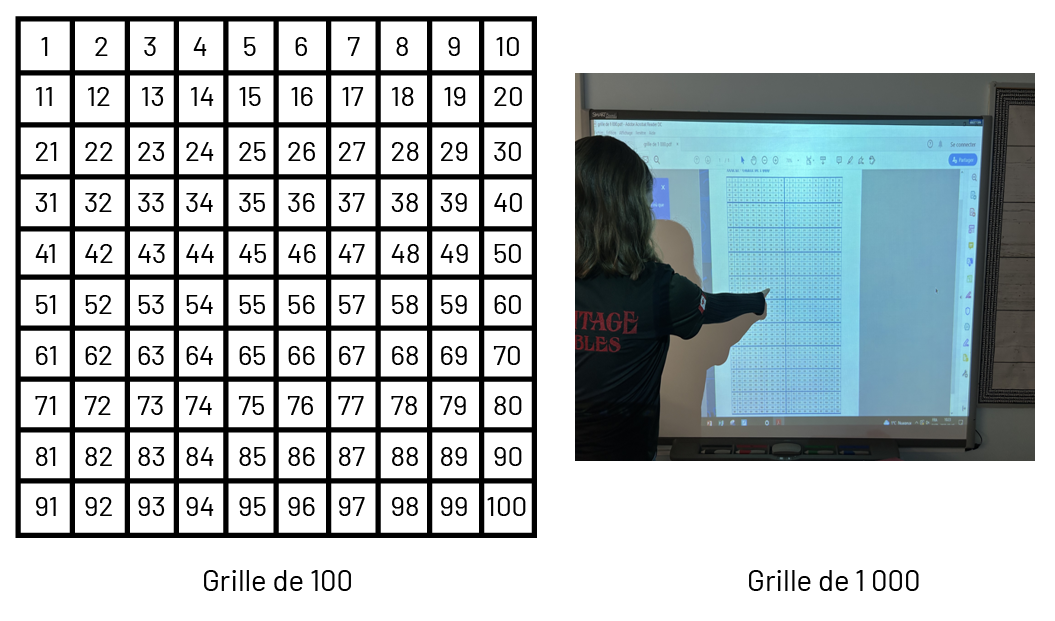
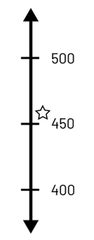
Droite numérique : Au cycle primaire, les élèves utilisent et construisent des droites numériques pour compter par intervalles ou pour identifier le nombre de dizaines dans un nombre. Au cycle moyen, l’utilisation et la construction de droites numériques variées permettent aux élèves de représenter de grands nombres et de reconnaître les relations entre eux. Voici quelques exemples de droites numériques sur lesquelles le nombre 457 est représenté :
- droite numérique dont l’échelle est par intervalles de 250;
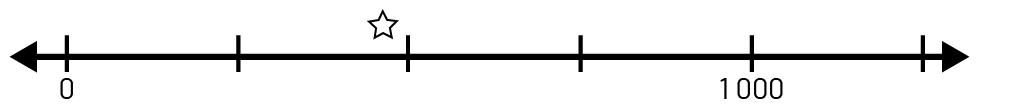
- droite numérique qui ne commence pas à 0, dont l’échelle est par intervalles de 20;
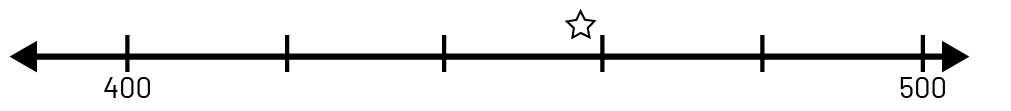
- droite numérique ouverte (qui n’est pas graduée) sur laquelle les nombres sont placés en relation les uns avec les autres;
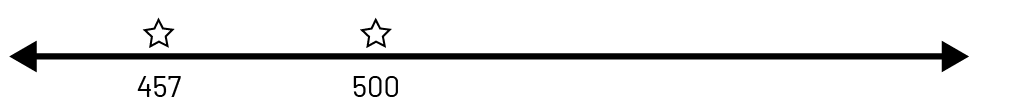
- droite numérique verticale qui présente les nombres en ordre croissant vers le haut et qui fait des liens avec les autres domaines, dont Sens de l’espace (par exemple, thermomètre) et Données (par exemple, axe des ordonnées).
Représentations symboliques
Les nombres sont représentés symboliquement à l’aide des chiffres qui les composent. Ils s’écrivent de gauche à droite par tranches de trois chiffres qui constituent les billions, les milliards, les millions, les milliers et les unités. Chacune des tranches regroupe les centaines (c), les dizaines (d) et les unités (u).
 image Les nombres représentés par tranches : de gauche à droite : billions, milliards, millions, milliers, unités.Chaque tranche regroupe les centaines (parenthèse ouvrante) « c » (parenthèse fermante), les dizaines (parenthèse ouvrante) d (parenthèse fermante), et les unités (parenthèse ouvrante) u (parenthèse fermante).
image Les nombres représentés par tranches : de gauche à droite : billions, milliards, millions, milliers, unités.Chaque tranche regroupe les centaines (parenthèse ouvrante) « c » (parenthèse fermante), les dizaines (parenthèse ouvrante) d (parenthèse fermante), et les unités (parenthèse ouvrante) u (parenthèse fermante).
Note : En français, l’écriture des nombres se fait en ajoutant un espace entre les tranches de trois chiffres (par exemple, 13 567 232) alors qu’en anglais, on sépare ces tranches à l’aide d’une virgule. Quoique l’écriture des nombres à quatre chiffres sans utiliser d’espace soit acceptée (par exemple, 3543), l’écriture avec un espace (par exemple, 3 543) est privilégiée.
L’écriture des grands nombres nécessite une bonne maîtrise du concept de valeur de position, faute de quoi l’élève à qui l’on demande d’écrire symboliquement « mille deux cent treize » pourrait écrire 1 000 200 13 ou 1 000 213 ou 1 200 13. Elle nécessite aussi une compréhension du rôle du zéro pour indiquer l’absence d’une quantité dans une des positions.
Voici un exemple d’un raisonnement que les élèves pourraient utiliser pour représenter symboliquement un grand nombre tel que six mille quatre cents :
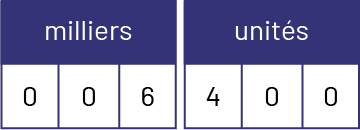
- six milles est représenté par 6 dans la tranche des milliers, mais il faut insérer un 0 dans la position des centaines et dizaines de mille, car le mot « cent » n’est pas entendu dans cette tranche du nombre ni « dix »;
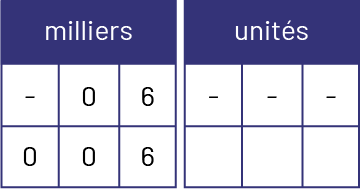
- quatre cents est représenté par un 4 dans la position des centaines de la tranche des unités. Puisqu’il n’y a aucune indication pour la position des dizaines et des unités, il faut ajouter deux 0 pour combler ces positions.

- six mille quatre cents écrit symboliquement donne 6 400.

Un nombre peut être représenté de différentes façons à l’aide de symboles mathématiques, soit en respectant la valeur de la position de chaque chiffre (1 236 est égal à \(1\;000\; + \;200\; + \;30\; + \;6\)), soit d’après quelques valeurs de position (1 236 est égal à 12 centaines et 36 unités) ou encore en effectuant différentes opérations (1 236 est égal à \(1\;000\; + \;236\) ou \(1\;240\; - \;4\;{\rm{ou}}\;{\rm{1}}\;{\rm{200}}\;{\rm{ + }}\;{\rm{36}}\;{\rm{ou}}\;{\rm{1}}\;{\rm{000}}\;{\rm{ + }}\;{\rm{100}}\;{\rm{ + }}\;{\rm{100}}\;{\rm{ + }}\;{\rm{15}}\;{\rm{ + }}\;{\rm{15}}\;{\rm{ + }}\;{\rm{6}}\)). En fait, il existe une infinité de façons de représenter un nombre, chacune permettant aux élèves de se donner une autre façon de l’interpréter et d’en comprendre le sens.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 64-72.
Il est important d’utiliser du matériel concret (tapis de valeur de position, matériel de base 10, abaques) et un questionnement efficace afin de permettre à l’élève de développer un sens du nombre.
Au cycle moyen, l’utilisation des cadres à 10 cases selon le principe de regroupement (groupes de 10) s’avère une autre façon de représenter la valeur des chiffres qui composent les grands nombres.
Exemple
1 256 représenté sur un tapis de valeur de position, à l’aide de matériel de base 10 et à l’aide d’un tableau de valeur de position
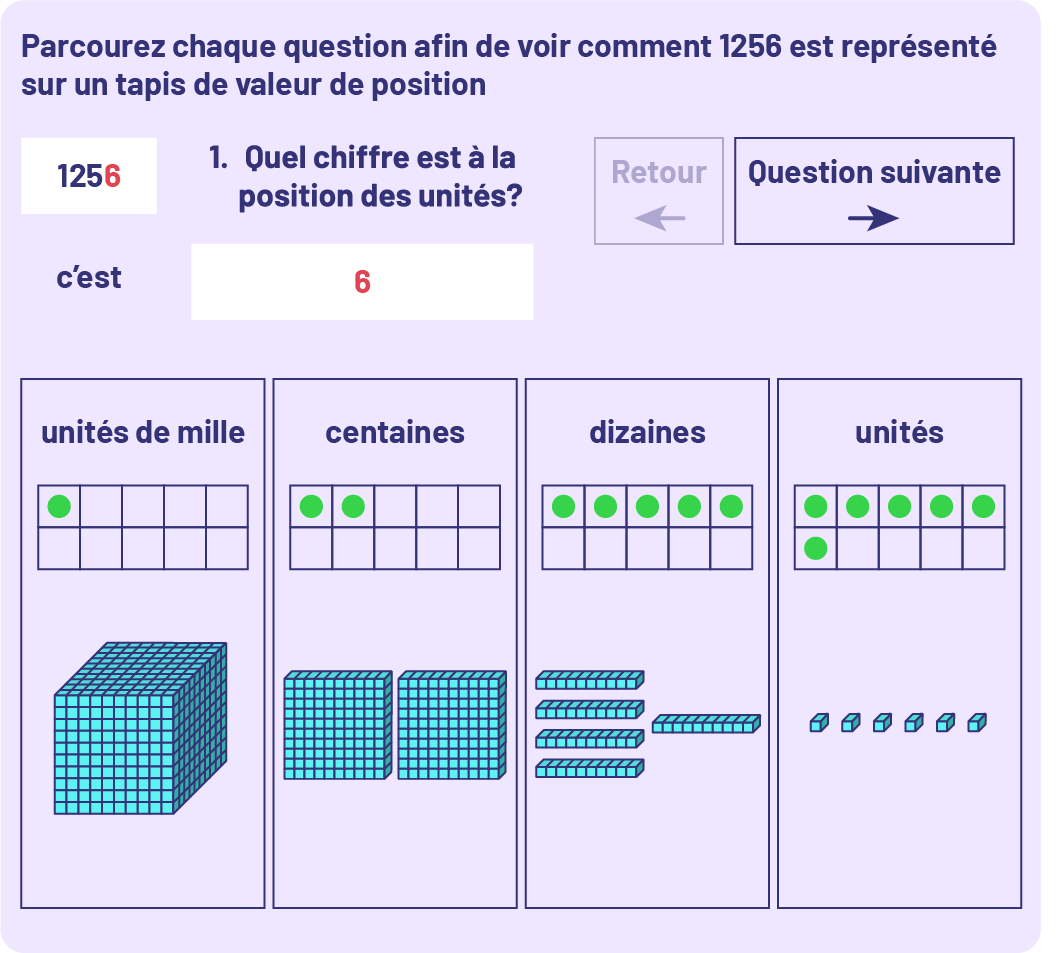 image Parcourez chaque question afin de voir comment 1256 est représenté sur un tapis de valeur de position.1256, quel chiffre est à la position des unités? C’est 6.Retour ou question suivante.Unités de mille, un point dans la grille de dix cases. Un bloc de mille unités.Centaines, 2 points dans la grille de dix cases, 2 planchettes de 100.Dizaines, 5 points dans la grille de dix cases, 5 réglettes de dizaines.Unités, 6 points dans la grille de dix cases, 6 blocs d’unités.
image Parcourez chaque question afin de voir comment 1256 est représenté sur un tapis de valeur de position.1256, quel chiffre est à la position des unités? C’est 6.Retour ou question suivante.Unités de mille, un point dans la grille de dix cases. Un bloc de mille unités.Centaines, 2 points dans la grille de dix cases, 2 planchettes de 100.Dizaines, 5 points dans la grille de dix cases, 5 réglettes de dizaines.Unités, 6 points dans la grille de dix cases, 6 blocs d’unités.
| unités de mille | centaines | dizaines | unités |
|---|---|---|---|
| 1 256 | |||
| 125 | 6 | ||
| 120 | 56 | ||
| 12 | 5 | 6 | |
| 12 | 56 | ||
| 10 | 25 | 6 | |
| 10 | 256 | ||
| 1 | 2 | 5 | 6 |
| 1 | 25 | 6 | |
| 1 | 256 |
Source : L’@telier – Ressources pédagogiques en ligne (atelier.on.ca)
Habileté : composer et décomposer les nombres naturels de 0 jusqu’à 10 000
Les nombres peuvent être composés et décomposés de diverses façons, y compris à l’aide de la valeur de position.
Les nombres peuvent être composés en combinant au moins deux nombres pour créer un plus grand nombre. Par exemple, 1 300, 200 et 6 sont combinés pour faire 1 506.
Les nombres peuvent être décomposés en les représentant comme une composition d’au moins deux plus petits nombres. Par exemple, 5 125 peut être représenté par 2 500 et 2 500 et 100 et 25.
Lorsqu’un nombre est décomposé puis recomposé, la quantité reste inchangée. C’est le principe de conservation du nombre.
Il existe plusieurs façons de décomposer un nombre à l’aide de la valeur de position, et elles aident grandement à comprendre les liens entre les valeurs de position et à approfondir le sens du nombre. Par exemple, 587 pourrait être décomposé en 58 dizaines et 7 unités ou en 50 dizaines et 87 unités.
Composer et décomposer les nombres de diverses façons permettent aux élèves de développer des stratégies de calcul mental efficaces et de faire des comparaisons.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Afin d’accroître leur sens du nombre, les élèves du cycle moyen doivent « jouer avec les nombres », c’est-à-dire qu’elles et ils doivent manipuler les nombres, les décomposer et les regrouper pour découvrir les principales caractéristiques de ces nombres et les relations qui existent entre eux. Ces activités permettent aussi aux élèves de découvrir plusieurs relations entre les opérations arithmétiques.
Il n’est pas question de chercher à faire en sorte que les élèves reconnaissent toutes les relations entre les nombres dans une situation donnée. L’accent doit plutôt être mis sur l’habileté à repérer les relations les plus pertinentes qui leur permettront de traiter efficacement ces nombres en contexte.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 43.
Relations d’égalité
Un nombre est représenté symboliquement à l’aide de chiffres. Par exemple, le nombre mille deux cent cinquante-six écrit symboliquement donne 1 256. Il peut aussi être représenté à l’aide de diverses expressions numériques. Par exemple, la représentation \(1\;000\; + \;200\; + \;50\; + \;6\) permet de reconnaître 1 256 en fonction de la valeur de position des chiffres qui le composent. Il y a de nombreuses autres façons de décomposer ou de représenter ce nombre.
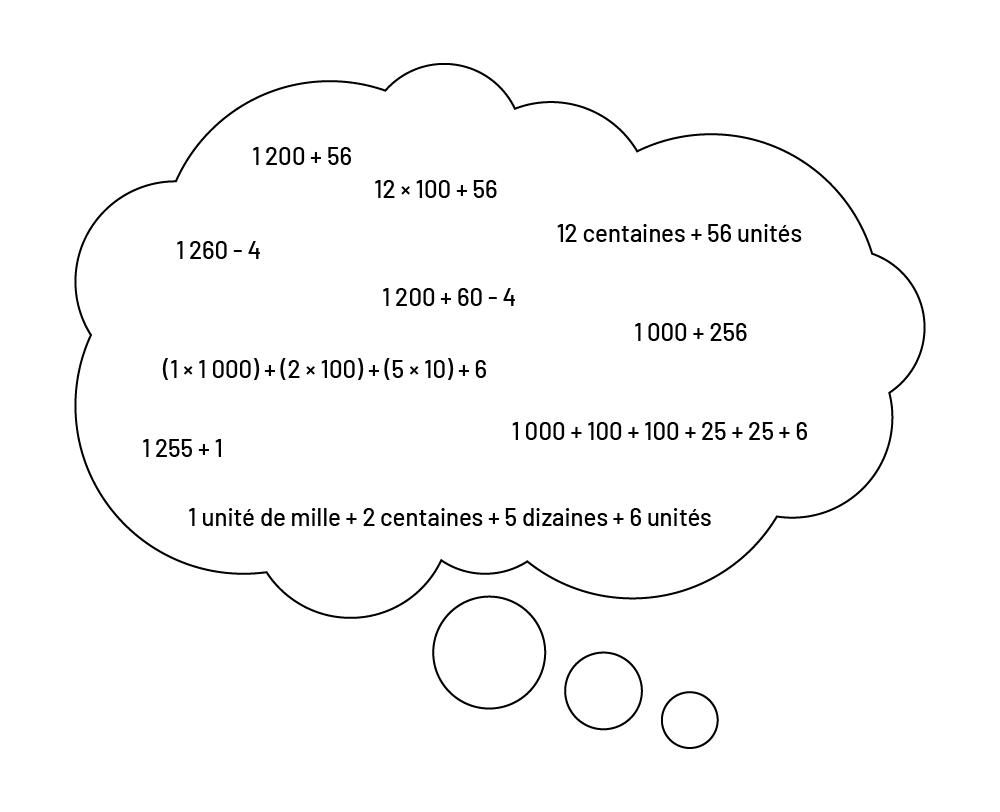 image Dans une bulle de pensée, on retrouve les expressions mathématiques suivantes :1200 plus 56.12 multiplié par 100 plus 56.1260 moins 4.1200 plus 60 moins 4.12 centaines plus 56 unités.1000 plus 256.(Parenthèse ouvrante) un multiplié par 1000(parenthèse fermante) plus (parenthèse ouvrante) 2 multiplié par 100 (parenthèse fermante) plus (parenthèse ouvrante) 5 multiplié par dix (parenthèse fermante) plus 6.1255 plus un.1000 plus 100 plus 100 plus 25 plus 25 plus 6.Une unité de mille plus 2 centaines plus 5 dizaines plus 6 unités.
image Dans une bulle de pensée, on retrouve les expressions mathématiques suivantes :1200 plus 56.12 multiplié par 100 plus 56.1260 moins 4.1200 plus 60 moins 4.12 centaines plus 56 unités.1000 plus 256.(Parenthèse ouvrante) un multiplié par 1000(parenthèse fermante) plus (parenthèse ouvrante) 2 multiplié par 100 (parenthèse fermante) plus (parenthèse ouvrante) 5 multiplié par dix (parenthèse fermante) plus 6.1255 plus un.1000 plus 100 plus 100 plus 25 plus 25 plus 6.Une unité de mille plus 2 centaines plus 5 dizaines plus 6 unités.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 48.
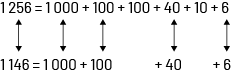
La forme développée (par exemple, \(4\;187 = 4\;000 + 100 + 80 + 7\) ou \(4 \times 1\;000 + 1 \times 100 + 8 \times 10 + 7 \times 1\)) est utile pour montrer les liens avec la valeur de position.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Les relations d’égalité permettent d’établir l’équivalence entre diverses représentations d’une même quantité. L’exploration des multiples représentations d’un nombre aide les élèves à acquérir une meilleure compréhension du sens de ce nombre. En situation de résolution de problèmes, les élèves doivent apprendre à choisir la représentation la plus appropriée au contexte et à l’intention.
Voici quelques exemples :
Pour calculer
\(\ 25\; \times \;9\; = \;25\; \times \;(10\; - \;1)\)
\(\ 25\; \times \;9\; = (25\; \times 10) \; - ( 25\; \times \;1)\)
\(\ 25\; \times \;9\; = \;250\; - \;25\)
Alors \(\;25\; \times \;9\; = \;225\)
Pour faire un calcul mental
\(\begin{array}{l}325\; + \;527\; = \;325\; + \;525\; + \;2\\325\; + \;527\; = \;850\; + \;2\\325\; + \;527\; = \;852\end{array}\)
Pour estimer
\(\ 24\; \times \;26\) est près de \(\ 25\; \times \;25\)
\(\ 25\; \times \;25\) = \(\ 25 \times (20\; + \;5)\)
\(\ 25\; \times \;25\) = \(\ (25\; \times \;20) + (25\; \times \;5)\)
\(\ 25\; \times \;25\; = \;500\; + \;125\)
\(\ 25\; \times \;25\; = \;625\)
Ainsi, on peut donc dire que \(\ 24\; \times \;26\) est environ 625.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 49.
Habileté : décrire de quelles façons les nombres sont utilisés dans la vie quotidienne
Le contexte est l’ensemble des informations entourant une situation donnée. Ces informations aident à cerner la situation dans laquelle les quantités sont utilisées et facilitent l’exercice d’un regard critique sur les nombres en question. En outre, le contexte facilite l’établissement de liens entre les nombres, les concepts mathématiques et le monde mathématisé. Pour toutes ces raisons, on préconise l’exploration des mathématiques en situation de résolution de problèmes.
Que veut dire 2 014 au juste? On parle de 2 014 « quoi »? Bref, un nombre sans contexte a peu de sens. C’est pourquoi on doit lui adjoindre des unités (2 014 jetons, personnes, billes, centimètres…) si on veut qu’il soit compris. Les élèves du cycle primaire ont déjà réalisé des activités avec les nombres dans différents contextes en utilisant diverses unités. Au cycle moyen, on doit maintenir cette contextualisation afin de développer le sens des quantités, et ce, avec des nombres dans les milliers et les millions.
Un pas important à franchir est d’amener les élèves à comprendre que le même nombre représente la même quantité même si les contextes sont différents. Le nombre n’est qu’une représentation symbolique de la quantité. Si l’on a 1 000 pommes, 1 000 battements de cœur ou 1 000 immeubles, la quantité qu’est le regroupement de mille ne change pas. Pourtant, si on demande aux élèves si elles et ils croient qu’il y a plus de pommes que d’immeubles, un bon nombre risque de répondre qu’il y a plus d’immeubles que de pommes. Les élèves se sont attardés à l’espace occupé par les objets plutôt qu’à la quantité d’objets (1 000).
Il faut aussi que les élèves reconnaissent que selon le contexte de la situation donnée, différentes interprétations peuvent être dégagées d’une même quantité. Par exemple, pour des jeunes, une somme de 100 $ peut représenter beaucoup d’argent. Cependant, en contexte, le sens du nombre invite à nuancer : c’est beaucoup pour le prix d’un chandail, mais peu pour celui d’une bicyclette neuve. Le contexte change, mais la quantité demeure inchangée. De même, 100 000 blocs de bois représentent beaucoup de blocs, alors que 100 000 cheveux sur la tête équivalent à une chevelure moyenne. Ou encore, les élèves peuvent considérer que 13 ne représente pas une grande quantité, mais si on ajoute qu’il est le nombre de nos frères et sœurs, il prend une tout autre valeur. Ces exemples concrets et simples incitent à réfléchir et à analyser les quantités de façon critique.
Au cycle moyen, la compréhension des nombres en contexte devient de plus en plus importante. Les élèves doivent commencer à porter des jugements critiques quant aux quantités et à faire preuve de discernement par rapport aux nombres. Les activités d’apprentissage doivent donc aider les élèves à développer d’autres habiletés, telles que reconnaître la vraisemblance d’un nombre donné, reconnaître qu’il s’agit d’une valeur exacte, ou au contraire, reconnaître qu’il s’agit d’un nombre approximatif provenant d’une estimation ou même d’un arrondissement. Le développement de ces habiletés peut être amorcé en ayant en classe des échanges sur le sens de nombres provenant de journaux et en discutant de leur signification réelle et de leur pertinence.
Le contexte permet aussi de reconnaître qu’un même nombre n’a pas toujours le même sens. En effet, lorsqu’il est question de nombres, l’interprétation courante les associe à la quantité, soit aux nombres cardinaux. Pourtant, en examinant le contexte, on remarque que certains nombres ne représentent pas des quantités, mais une position. C’est le cas des nombres ordinaux. Par exemple, lors d’un marathon, la coureuse ou le coureur qui est à la position 1 582 ne compte pas 1 582 objets. Le chiffre indique la position d’une seule personne dans la série donnée. Les chiffres et les nombres sont aussi utilisés comme code d’identification. Les numéros d’assurance sociale, de codes à barres, de plaques d’immatriculation et d’adresses appartiennent à cette catégorie.
 image Photo un: 1000000 grains de sable. Nombre cardinal. Un bac rempli avec du sable.Photo 2: Le coureur portant un chandail rouge à la droite de l’image est au mille cinq cent quatre-vingt-deuxième rang. Nombre ordinal. Une rue remplie de marathoniens.Photo 3: Code à barres. Code. Un code à barres tel que retrouvé sur des articles en magasin.
image Photo un: 1000000 grains de sable. Nombre cardinal. Un bac rempli avec du sable.Photo 2: Le coureur portant un chandail rouge à la droite de l’image est au mille cinq cent quatre-vingt-deuxième rang. Nombre ordinal. Une rue remplie de marathoniens.Photo 3: Code à barres. Code. Un code à barres tel que retrouvé sur des articles en magasin.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-32.
Connaissance : nombres naturels
Les nombres naturels sont tous les nombres entiers positifs, y compris le 0.
Exemple
0, 2, 17, 36, 134, etc.
Il y a une infinité de nombres naturels.
Notre système de base 10 est axé sur le regroupement (groupes de 10).
- Les unités sont regroupées en groupes de 10 pour former les dizaines.
- Les dizaines sont regroupées en groupes de 10 pour former les centaines, et ainsi de suite.
Source : L'@telier – Ressources pédagogiques en ligne (atelier.on.ca)
