B1.1 Read, represent, compose, and decompose whole numbers up to and including 10 000, using appropriate tools and strategies, and describe various ways they are used in everyday life.
Skill: Reading Whole Numbers Up To 10 000
Reading numbers involves interpreting them as a quantity when they are expressed in words, in standard notation, or represented using physical objects or diagrams.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
A student who can read or name a large number has not necessarily understood or grasped the meaning of the quantity that it represents. Number sense is not innate.
- It is developed during the primary grades through hands-on activities using concrete materials.
- It continues to be developed in the junior grades as students use their prior knowledge of the base ten system and apply it to larger numbers.
Teachers should provide students with a clear understanding of:
- the connections between the digits that make up a number;
- the value of the digits according to their position or place in the number;
- the quantity that the numbers represent.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
The Base Ten System
The base ten number system commonly used today in many countries uses 10 different symbols, namely the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. It is a positional system since the symbols are given different values depending on their position or place within a number. For example, the number 2 has a value of 2 ones (units) in the number 6742, while it has a value of 2000 ones (units) in the number 2487. Understanding the relationships between the value of digits and their position in a number is essential to the development of number sense. In the primary grades, students develop an understanding of the relationships between the place values of ones, tens and hundreds. However, in the Junior and Intermediate Divisions, students do not automatically transfer this understanding to larger numbers. Therefore, teachers must ensure that they understand that the value of any position in a number is always 10 times larger than the value of the position immediately to the right, and 10 times smaller than the value of the position immediately to the left. It is also important to examine the 100-fold or 1000-fold relationships between place value in order to develop students' deep number sense, including large number sense.

Students should also recognize, for example, that one (1) ten thousand represents a grouping of 100 hundreds, a grouping of 1000 tens, or even a grouping of 10 000 ones. These groupings allow students to recognize equivalent representations of numbers (for example, 2534 is equal to 25 hundreds and 34 ones).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 44-45.
It is important that students understand that a zero in the number indicates that there are no group or quantity at that place value. It serves as a placeholder and keeps the other numbers in their correct "position".
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8 , 2020, Ontario Ministry of Education.
Number is an abstract representation of a very complex concept. For this reason, the relationship between the way a number is named and the quantity it represents is not obvious to students. Many adults mistakenly believe that if students can count, they understand the meaning of each number. However, a student may well be able to read and name a number, for example, fifty-eight thousand, without really having a sense of the quantity it expresses.
Teachers should support students in making connections between the base ten number system and how numbers are named and written.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 65.
One strategy that encourages the association of the number with the quantity it represents is to emphasize the place value of each of the digits that make up a number when naming it (for example, instead of reading the number 62 098 as sixty-two thousand ninety-eight, students can say 6 groups of 10 000, 2 groups of 1000, 9 groups of 10, and 8 groups of one) or certain regroupings (for example, 62 groups of 1000 and 98 groups of one).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 70.
Mental Representations
The mental representation of a quantity is the image, developed through thinking, of a number. When students hear and read a number, they need to "see" the quantity that the number represents and understand the "how much".
It is therefore important that students have mental representations of different numbers in different contexts. For example, consider the number 2000, which can be mentally represented by 2 grids of 1000 or 20 grids of 100, by the number of seats in a lecture hall, by 40 school buses carrying 50 students, and so on.
It is important for students to develop a variety of mental representations for numbers. These visualizations may simply represent quantities. For example, the "how many" of 10 000 may generate a mental representation of 10 grids of 1000. However, the presence of units in a situation may promote a different, more precise mental representation that would be related to a given situation. For example, students may visualize that 5000 can be represented by 100 parked cars in 50 parking lots or 10 schools with 500 students.
In addition, if the context suggests it, students can look critically at the quantity (for example, determine whether it is "a lot" or "a little"). The mental representation will then be coloured by the context. For example, the mental representation of 100 people at a family party is not the same as 100 people in a crowd at a hockey game. The various mental representations are all valid; they depend primarily on the context of the situation and the students' sense of number. The mental representation remains personal, but the ease with which an individual can visualize numbers is an indicator of their number sense.
In order to develop mental representations, students use different strategies that respond to various situations and needs. With very small numbers, it is possible for them to use subitizing, that is, to recognize small quantities without having to count each of the objects. To recognize larger quantities, students will use other strategies. For example, counting each pea in a package of peas can be laborious, so combining can be used.

Thus, after counting 10, they can see that there are 3 equal sets for a total of 30 peas. In this case, the counting strategy (10) is combined with the subitizing strategy (3 sets). As we move along, students will increasingly use combining to understand quantity. Thus, students will create mental representations by visualizing equal groupings, for example, visualizing 30 as 3 sets of 10 peas.
The mental representation of large numbers can hardly be done by recognizing the elements individually. However, it can be created by using cues that are related to a large quantity (for example, recognizing that 6000 people is about three times the number of spectators in an amphitheater with 2000 seats).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 29-31.
Benchmark Numbers
In general, a benchmark is a mark, a milestone, a reference. As part of the development of a sense of number, the use of benchmark numbers promotes mental representation and thus facilitates the understanding of number and the notion of "how much". The benchmark numbers, without which it is difficult to understand quantity, are numbers or quantities that can be easily represented mentally since they have already been seen and manipulated. Students will have difficulty understanding quantity if benchmark numbers are not used. For example, when reading from a book of records, students see numbers associated with text. Students grasp that the quantities mentioned are of an impressive order of magnitude, but often do not have the true meaning of these quantities, as they do not connect these numbers to meaningful benchmark numbers for them. Such is the case of a student who reads the following excerpt:

The student may react to this fact and finds it extraordinary, without relating the quantity 10.8 kg to a benchmark. This fact is extraordinary because it is a "record", but the student grasp that it is probably more than double their own birth weight? Does the student have any understanding of how big a 10.8 kg baby really is?
As a result of experiences (for example, studying money, counting in intervals of 200, 250, 500, and 1000) and learning about and internalizing number relationships (for example, knowing that 4 x 250 = 1000, 1000 = 2 x 500, 5 x 200 = 1000) can support the development of 200, 250, 500, and 1000 as benchmark numbers. Thus, 3200 can be understood as 2500 plus 700 or 2500 plus 500 plus 200, and the number 8000 can be quickly associated with 4 groups of 2000.
Although the majority of students entering Grade 4 can read and write numbers to 1000 symbolically, they do not necessarily understand the quantity represented by these large numbers. By creating benchmarks and visualizing groupings, students will develop a better understanding of the concept of quantity represented by large numbers.
Benchmark numbers are particularly useful for understanding large numbers, since it is usually impossible to recognize these quantities globally or to grasp them by counting. Students need to get a sense of them by comparing them with a benchmark number. For example, the school just received 10 000 sheets for photocopying. Should the custodian ask for help carrying them? In order for students to truly understand the situation and the quantity involved, they need to create a mental image of what 10 000 sheets might represent. Using a package of 500 sheets as a guide, students can imagine this quantity and apply the proportionality relationship to deduce that 2 packages contain 1000 sheets. Therefore, 10 000 sheets would be 10 times as many packages, or 20 packages of sheets. We can even recognize that 20 packages are equivalent to 2 boxes of paper. The mental representation of the space occupied by these 10 000 sheets then becomes possible. The answer to the original question, whether the custodian should ask for help in carrying the sheets, can then be debated with full knowledge.
Students should develop their own personalized benchmarks, depending on the context and the numbers being dealt with. There is no list of benchmarks. They are personal and come from making them meaningful and easier to use. However, real-life situations provide teachers with ample opportunity to draw their students' attention to the quantity and creation of benchmarks.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 33-35.
Skill: Representing Whole Numbers Up to 10 000
Students need to learn to represent numbers in a variety of ways and to recognize them in their multiple representations. These skills help them make connections between a number, its representation, and the quantity it represents. It is therefore essential that students be exposed to different representations of numbers. It is also important that students be exposed to a variety of contexts that lead them to represent a number in each of the representations shown in the following diagram, as well as to move from one representation to another.
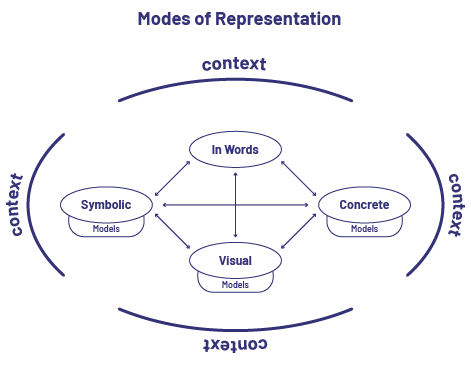
Teachers need to be aware of the order in which they should introduce these four modes of representation with students. Baroody and Coslick (1998, pp. 3-8 to 3-16) suggest that a new concept be presented in a real and meaningful context so that students can first create representations using words, followed by concrete and visual representations. Only when students have developed some understanding of the concept can they move on to its symbolic representation. Students should be able to make connections between representations and move easily from one representation to another.
Representations Using Words
In Grade 4, students learn to read and write numbers up to 10 000 in words. The challenges of writing numbers in words should not be underestimated. To help students overcome these challenges, teachers should include numbers on the word wall and build reference materials with them.
Concrete Representations
Using manipulatives (for example., counters, base ten materials) to represent numbers helps students develop number sense.

A word of caution is in order when it comes to using manipulatives. It is important to recognize that these materials represent a mathematical concept, not the concept itself; for example, the flat is not a hundred, but it represents a hundred small cubes.
The danger is that students will use the manipulative mechanically without making the connections to the underlying mathematical concepts. For this reason, teachers must ensure that there is real learning and not just blind use of the model. For example, it is easy for students to fill in the blanks in the sentence below the picture by looking at the place value mat.
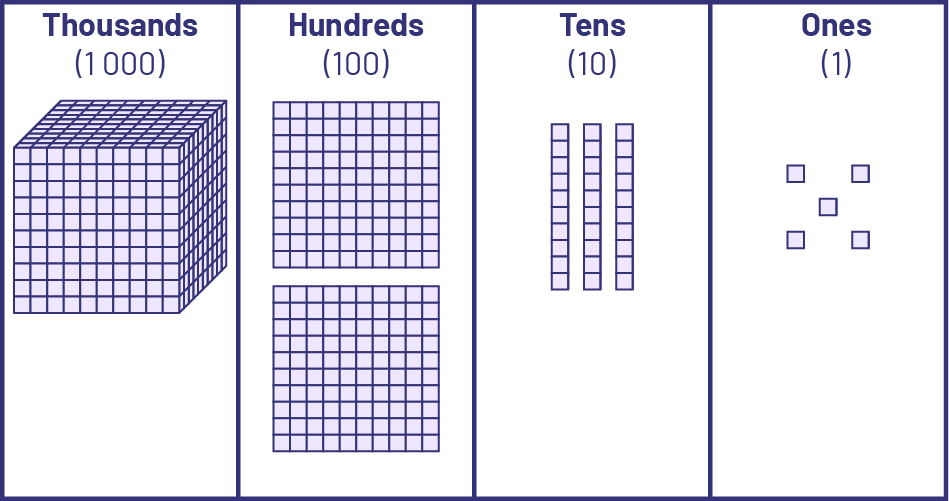
The representation is ____thousands, ____ hundred(s), ___ten(s) and ____ones
Do students understand that there are also one thousand two hundred and thirty-five small cubes or ones on the carpet and that this is one of the realities that is represented by the number 1235? It is important to ask students to explain in different ways what is represented. For example, 1235 is also 1200 ones and 35 ones or 123 tens and 5 ones.
Another way to check for understanding is to ask students how many hundreds there are in 1235. Many students will tend to say that there are 2. It is important to clarify that the number in the hundreds position is a "2", but that the number 1235 is made up of 12 hundreds (12 groupings of 100 units = 1200). These 12 hundreds can be "seen" by breaking down the large cube into 10 flats and adding them to the 2 flats that are in the hundreds column.
Using the place value mat, we notice that even though numbers are written from left to right, they are formed from right to left: ones grouped together form tens, tens grouped together form hundreds, and so on. Once the counting is finished, we write the number starting from the left.

The choice of materials available to students can also make a difference in their development of conceptual understanding. There are a variety of commercial materials available to represent numbers: marbles, interlocking cubes, or any other object that can be used to count. Some of these materials clearly and concretely represent the magnitude relationship between ones, tens, hundreds… (for example, the base ten blocks used in the photos above). However, with other materials, this relationship is represented in a more abstract way. For example, on an abacus or a place value flip chart, the grouping is represented according to the position of the digit from left to right, as in symbolic writing of numbers.

By exposing students to a variety of manipulatives, teachers can help them develop a better understanding of numbers.
Visual (Semi-Concrete) Representations
Students can also represent numbers with visuals (for example, illustration, hundreds chart, number line).
Illustration: A number can be represented with drawings in order that show certain groupings or parts that compose it. For example, the number 376 can be illustrated by groupings as follows:
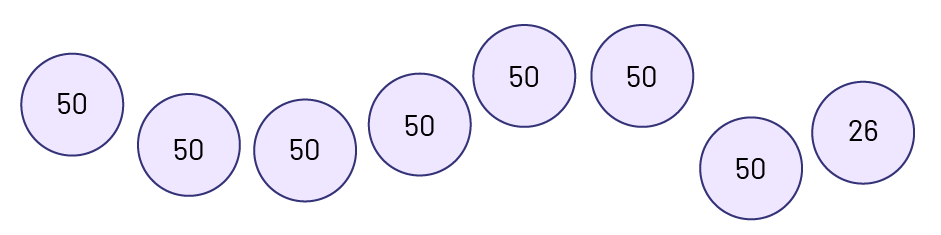
Illustration can also be related to manipulatives (hence the term "semi-concrete").

Hundreds Chart: The hundreds chart is widely used in the primary grades. Although more difficult to manipulate, a thousands chart can help students in the junior grades to better understand numbers by allowing them to compare and contrast them.

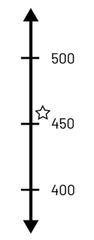
Number Lines: In the primary grades, students use and construct number lines to skip count or to identify the number of tens in a number. In the junior grades, the use and construction of a variety of number lines allows students to represent large numbers and recognize the relationships between them. Examples of number lines with the number 457 on them include the following:
- a number line with a scale of 250;
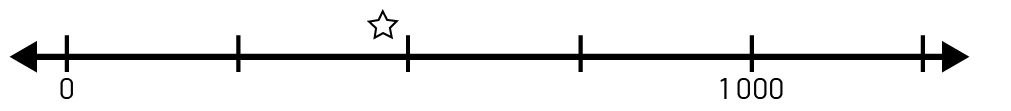
- a number line that does not start at 0, with a scale of 20;

- an open number line (not partitioned or divided) on which numbers are placed in relation to each other;
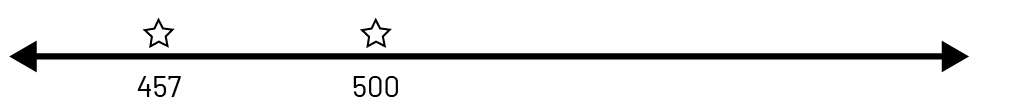
- a vertical number line with numbers in ascending order upward and has applications in other areas, including Sense of Space (for example, thermometer) and Data (for example, y-axis).
Symbolic Representations
Numbers are represented symbolically by the digits that make them up. They are written from left to right in three-digit increments, called perios, that make up the trillions, billions, millions, thousands and ones. Each of the brackets includes the hundreds (h), tens (t) and ones (o).

Note: In English as well as in French, numbers are written by adding a space between the 3-digit periods (for example, 13 567 232). Although writing 4-digit numbers without using a space is accepted (for example, 3543).
Writing large numbers requires a good grasp of place value, otherwise a student asked to write symbolically "one thousand two hundred and thirteen" might write 1 000 200 13 or 1 000 213 or 1 200 13. It also requires an understanding of zero as a placeholder to indicate the absence of a quantity in one of the positions.
The following are examples of reasoning that students could use to symbolically represent a large number such as six thousand four hundred:
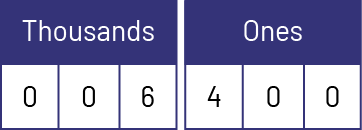
- six thousand is represented by 6 in the ones place of the thousands period, and a 0 is inserted in all three places of the ones period;
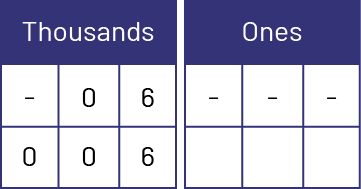
- four hundred is represented by a 4 in the hundreds place of the ones period. Since there was nothing that came after four hundred, two 0's must be added to fill the tens and ones places.

- six thousand four hundred written symbolically gives 6400.

A number can be represented in different ways using mathematical symbols, either by respecting the value of the position of each digit (1236 equals 1000 + 200 + 30 + 6), using variations of place value (1236 equals 12 hundreds and 36 ones) or by performing different operations (1236 equals 1000 + 236 or 1240 - 4 or 1200 + 36 or 1000 + 100 + 100 + 15 + 15 + 6) . In fact, there are an infinite number of ways to represent a number, each of which allows students to develop a different way of interpreting it and understanding its meaning.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 48, 64-72.
It is important to use concrete materials (place value mats, base ten materials, abacuses) and effective questioning to allow the student to develop a sense of number.
Ten Frames: In the junior grades, the use of ten frames is another way to represent the value of the digits that make up large numbers.
Example
1256 represented using place value mat, ten frames and base 10 materials
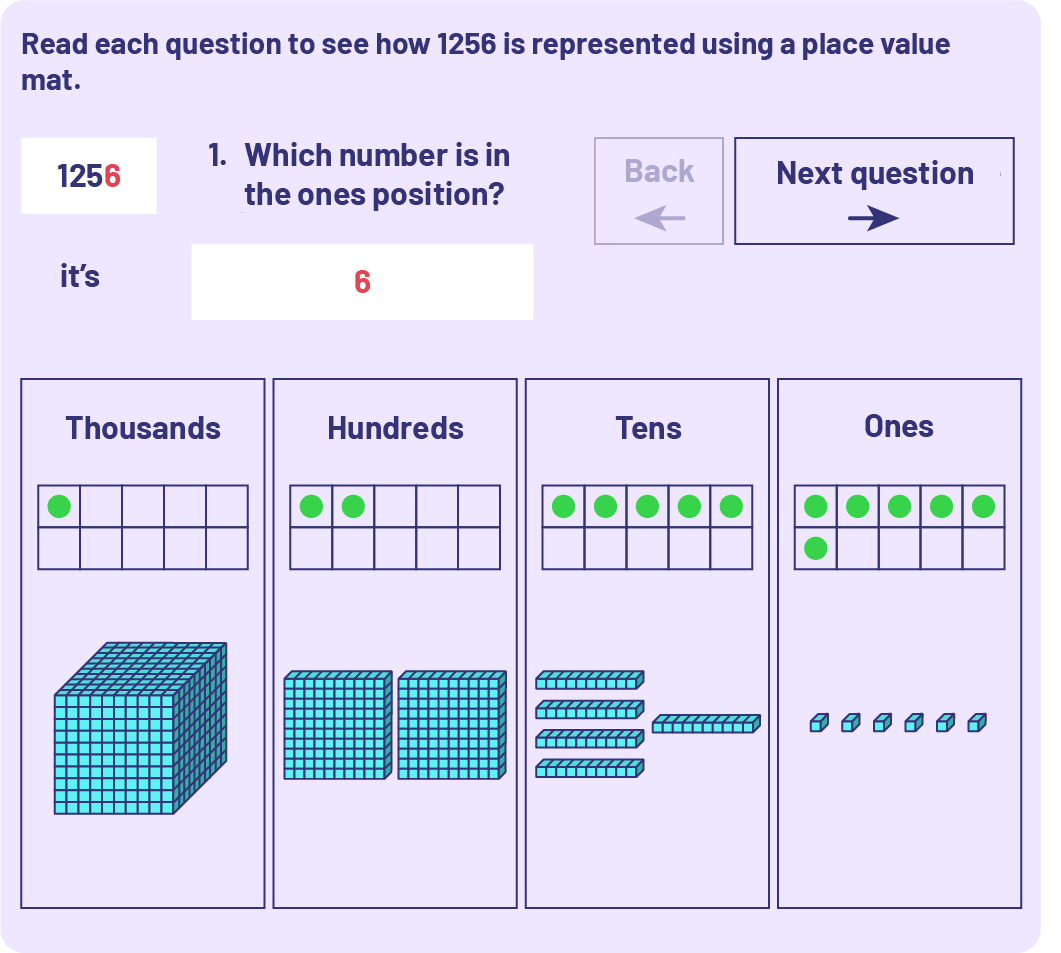
Source: translated from L’@telier – Ressources pédagogiques en ligne (atelier.on.ca).
| Thousands | Hundreds | Tens | Ones |
|---|---|---|---|
| 1 256 | |||
| 125 | 6 | ||
| 120 | 56 | ||
| 12 | 5 | 6 | |
| 12 | 56 | ||
| 10 | 25 | 6 | |
| 10 | 256 | ||
| 1 | 2 | 5 | 6 |
| 1 | 25 | 6 | |
| 1 | 256 |
Source: translated from L’@telier – Ressources pédagogiques en ligne (atelier.on.ca).
Skill: Composing and Decomposing Whole Numbers Up to 100 000
Numbers can be composed and decomposed in a variety of ways, including using place value.
Numbers can be made up by combining two or more numbers to create a larger number. For example, 1300, 200 and 6 are combined to make 1506.
Numbers can be decomposed by representing them as a composition of at least two smaller numbers. For example, 5125 can be represented by 2500 and 2500 and 100 and 25.
When a number is decomposed and then recomposed, the quantity is unchanged. This is the principle of conservation.
There are non-standard but equivalent ways to decompose a number using place value, based on understanding the relationships between the place values. For example, 587 could be decomposed as 58 tens and 7 ones or decomposed as 50 tens and 87 ones, and so on.
Composing and decomposing numbers in a variety of ways can support students in becoming flexible with their mental math strategies and to make comparisons between numbers.
Source: The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.
In order to develop their number sense, students in the junior grades should have many opportunities to "play with numbers" by manipulating, decomposing, and grouping numbers, which will help them to discern the key characteristics of numbers and the relationships among them. These activities also allow students to discover several relationships between operations.
The focus is not on getting students to recognize all the relationships between numbers in a given situation. Rather, the focus should be on the ability to identify the most relevant relationships that will allow them to deal effectively with those numbers in context.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 43.
Equality
A number is represented symbolically using digits. For example, the number one thousand two hundred fifty-six written symbolically gives 1256. It can also be represented using various numerical expressions. For example, the representation 1000 + 200 + 50 + 6) allows you to recognize 1256 according to the place value of the digits that make it up. There are many other ways to decompose or represent this number.
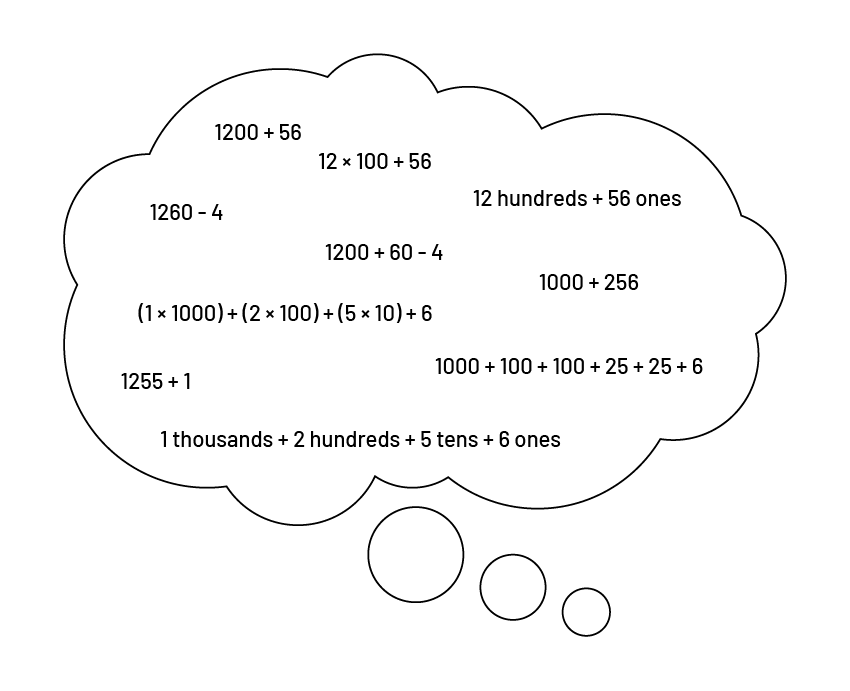
A number can be represented in expanded form (for example, 4187 = 4000 + 100 + 80 + 7 or 4 × 1000 + 1 × 100 + 8 × 10 + 7 × 1) to show place value relationships.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
The relationship of equality allows for equivalence between various representations of the same quantity. Exploring multiple representations of a number helps students develop a better understanding of the meaning of that number. In problem solving situations, students must learn to choose the most appropriate representation for the context and intent.
Some examples include:

To Calculate
\(\ 25\; \times \;9\; = \;25\; \times \;(10\; - \;1)\)
\(\ 25\; \times \;9\; = (25\; \times 10) \; - ( 25\; \times \;1)\)
\(\ 25\; \times \;9\; = \;250\; - \;25\)
Thus, \(\;25\; \times \;9\; = \;225\)
To Do Mental Math
\(\begin{array}{l}325\; + \;527\; = \;325\; + \;525\; + \;2\\325\; + \;527\; = \;850\; + \;2\\325\; + \;527\; = \;852\end{array}\)
To Estimate
\(\ 24\; \times \;26\) is close to \(\ 25\; \times \;25\)
\(\ 25\; \times \;25\) = \(\ 25 \times (20\; + \;5)\)
\(\ 25\; \times \;25\) = \(\ (25\; \times \;20) + (25\; \times \;5)\)
\(\ 25\; \times \;25\; = \;500\; + \;125\)
\(\ 25\; \times \;25\; = \;625\)
Thus, we can say that \(24 \times \;26\) is about 625.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 48-49.
Skill: Describing the Ways in Which Numbers are Used in Everyday Life
Context is all the information surrounding a given situation. This information helps to identify the situation in which quantities are used, and facilitates a critical view of the numbers in question. Context also facilitates the establishment of links between numbers, mathematical concepts and the mathematical world. For all these reasons, it is important for students to explore and learn mathematics through problem-solving situations.
What exactly does 2014 mean? We are talking about 2014 "what"? In short, a number without context has little meaning. Therefore, it must be accompanied by units (counters, people, marbles, centimetres…) if it is to be understood. Students in the primary grades have already engaged in number activities in a variety of contexts using a variety of units. In the junior grades, this contextualization needs to be maintained in order to develop a sense of quantity with numbers in the thousands.
An important step is to support students in understanding that the same number represents the same quantity even though the contexts are different. The number is the symbolic representation of the quantity. If one has 1000 apples, 1000 heartbeats, or 1000 buildings, the quantity that is one thousand does not change. Yet, if students are asked if they believe there are more apples than buildings, many are likely to respond that there are more buildings than apples. They have focused on the space occupied by the objects rather than the quantity of objects (1000).
Students should also recognize that depending on the context of the given situation, different interpretations can be made of the same quantity. For example, for young people, $100 may represent a lot of money. However, in context, the meaning of the number invites nuance: it is a lot for the price of a sweater, but not much for the price of a new bicycle. The context changes, but the quantity remains the same. Similarly, 100 000 blocks of wood is a lot of blocks, while 100 000 hairs on the head is the equivalent of an average head of hair. Or, students may consider that 13 is not a large quantity, but if we add that it is the number of our brothers and sisters, it takes on a whole new value. These simple, concrete examples encourage students to think about and critically analyze quantities.
In the junior grades, understanding numbers in context becomes increasingly important. Students need to begin to make critical judgments about quantities and to exercise discernment about numbers. Learning activities should therefore help students develop other skills, such as recognizing the reasonableness of a given number, recognizing that it is an exact value, or recognizing that it is an approximate number resulting from estimation or even rounding. The development of these skills can be initiated by having class discussions about the meaning of numbers from newspapers and discussing their actual meaning and relevance.
The context also allows us to recognize that the same number does not always have the same meaning. The most common interpretation associates them with a quantity, namely cardinal numbers. However, some numbers do not represent quantities, but rather a position, as in the case of ordinal numbers. For example, in a marathon, the runner who comes in 10th place is the 10th person to cross the finish line. Numbers can also be used to label or identify as is the case with social insurance numbers, bar codes, license plates, and addresses.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 31-32.
Knowledge: Whole Numbers
Whole numbers are all positive integers, including 0.
Example
0, 2, 17, 36, 134, etc.
There is an infinity of whole numbers.
Our base ten system is based on groupings of 10.
- The ones are grouped in groups of 10 to form the tens.
- The tens are grouped in groups of 10 to form the hundreds, and so on.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
