À vue d'oeil...

B1.4 Représenter des fractions à partir des demis jusqu’aux dixièmes à l’aide de schémas, d’outils et de la notation fractionnaire usuelle, et expliquer la signification du numérateur et du dénominateur.

Habileté : représenter des fractions à partir des demis jusqu’aux dixièmes à l’aide de schémas, d’outils et de la notation fractionnaire usuelle

---

Représentations à l’aide de modèles

À l’origine des difficultés des élèves avec les fractions, on retrouve trop souvent le peu d’importance accordée aux modèles concrets et semi-concrets. L’utilisation de modèles est essentielle à l’apprentissage des fractions et devrait se poursuivre tout au long du parcours scolaire. Or, parmi les modèles utilisés dans les écoles, le modèle du cercle est surexploité et souvent inapproprié dans certains contextes. Le personnel enseignant doit donc voir à ce que les élèves apprennent à représenter les fractions de diverses façons selon les contextes. En général, on se réfère à trois modèles, le modèle de surface, le modèle de longueur et le modèle d’ensemble, chacun pouvant prendre des allures variées selon les outils et les matériaux utilisés.

Modèle de surface

Dans ce modèle, une surface ou une région est divisée en parties équivalentes. En classe, les modèles circulaires (tarte ou pizza) et les modèles rectangulaires peuvent être reproduits sur du carton rigide, puis plastifiés et coupés pour les exercices individuels. Les mosaïques géométriques, les géoplans, le papier à points et le papier quadrillé sont également de bons outils qui s’avèrent parfois plus appropriés à des situations particulières. Avec ce matériel, on devrait encourager les élèves à plier, à superposer, à fractionner et à découper pour développer leur sens de la fraction.

La vidéo suivante explique la relation entre le tout et les parties, ainsi que la signification du numérateur et du dénominateur, dans un modèle de surface.

Voici des exemples de situations qui peuvent être représentées à l’aide d’un modèle de surface.

Situation à fraction manquante

Jared coupe une pizza en 6 parties égales. Il mange 2 morceaux. Quelle fraction de la pizza Jared a-t-il mangée? ($\frac{2}{6}$)

Représentation de la situation

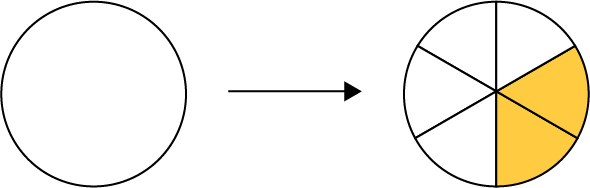
Situation à partie manquante

Colorie $\frac{3}{8}$ de ce rectangle.

Représentation de la situation

Situation à tout manquant

Voici $\frac{2}{8}$ d'un rectangle.

Dessine le rectangle en entier.

Représentation de la situation

image Un triangle rectangle divisé en 2 parties égales. Une flèche part de cette direction et pointe vers 4 triangles divisés en 2 parties égales, identiques au premier triangle. Les triangles sont superposés l’un contre l’autre de façon à former un carré avec 2 triangles et ensuite un rectangle en collant les 2 carrés. Une flèche part de cette direction et pointe vers un rectangle.

Modèle de longueur

Dans des situations qui portent sur la distance ou le temps, les modèles basés sur la longueur sont plus appropriés pour représenter les fractions (par exemple, réglettes, bandes de carton ou de papier, corde, segment de droite).

La vidéo suivante explique la relation entre le tout et les parties, ainsi que la signification du numérateur et du dénominateur, dans un modèle de longueur.

Voici des exemples de situations qui peuvent être représentées à l’aide d’un modèle de longueur.

Situation à fraction manquante

Lors d'un marathon de 15 km, Carlos a dû se retirer de la course au sixième kilomètre en raison d'une crampe. Quelle fraction du marathon avait-il complétée? ($\frac{2}{5}$ du marathon)

Représentation de la situation

Situation à partie manquante

Michel a coupé $\frac{2}{5}$ d'une corde de 10 m. De quelle longueur est son bout de corde? (4 m)

Représentation de la situation

Situation à tout manquant

Voici les $\frac{2}{3}$ d'un segment.

Trace le segment complet

Représentation de la situation

Modèle d’ensemble

L’utilisation d’un modèle d’ensemble requiert une bonne compréhension du concept de tout, puisque le tout n’est pas un élément, mais un ensemble d’éléments (par exemple, 12 objets). Les élèves ont du mal à comprendre ce modèle. Pourtant, il est nécessaire que les élèves se l’approprient, car on le retrouve dans beaucoup d’applications du quotidien. Souvent, les élèves ne saisissent le concept que superficiellement. Par exemple, d’un ensemble comprenant 9 jetons rouges et 6 verts, les élèves reconnaissent d’emblée que $\frac{9}{15}$ des jetons sont rouges, mais elles et ils ont de la difficulté à reconnaître que $\frac{3}{5}$ des jetons sont rouges à moins qu’on leur présente les jetons organisés en groupes de 3. Afin de bien comprendre le modèle d’ensemble, il est essentiel que les élèves aient l’occasion d’utiliser du matériel concret qu’elles et ils peuvent déplacer et regrouper.

La vidéo suivante explique la relation entre le tout et les parties, ainsi que la signification du numérateur et du dénominateur, dans un modèle d’ensemble.

Voici des exemples de situations qui peuvent être représentées à l’aide d’un modèle d’ensemble.

Situation à fraction manquante

Voici un ensemble de billes. Quelle fraction de l’ensemble est jaune? ($\frac{4}{6}$ des billes sont jaunes.)

Représentation de la situation

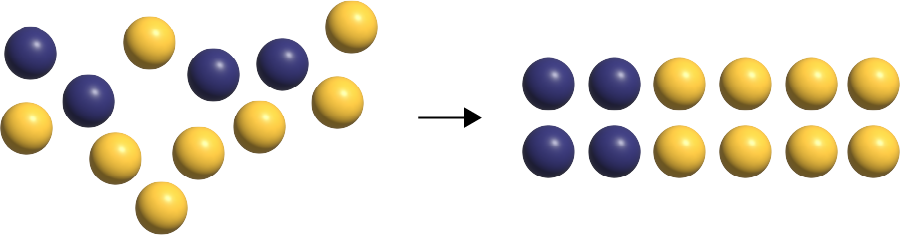
Note : $\frac{8}{12}$ et $\frac{2}{3}$ seraient aussi des fractions acceptables puisqu’elles sont équivalentes. Cette constatation ne doit pas découler de l’application d’un algorithme relié aux fractions équivalentes, mais des regroupements possibles des objets de l’ensemble.

Situation à tout manquant

Laurence collectionne des cartes de vedettes. À ce jour, Laurence a accumulé 36 cartes, soit $\frac{3}{4}$ des cartes de l'ensemble Nos vedettes préférées. Combien de cartes contient l'ensemble? (48 cartes)

Représentation de la situation

image 36 cartes dispersées. Une flèche partant de cette direction et allant vers 3 ensembles de 12 cartes chacun. Une flèche partant de cette direction et pointant vers un plus grand ensemble composé de 3 ensembles de 12 cartes chacun et d’un autre ensemble à part de 12 cartes.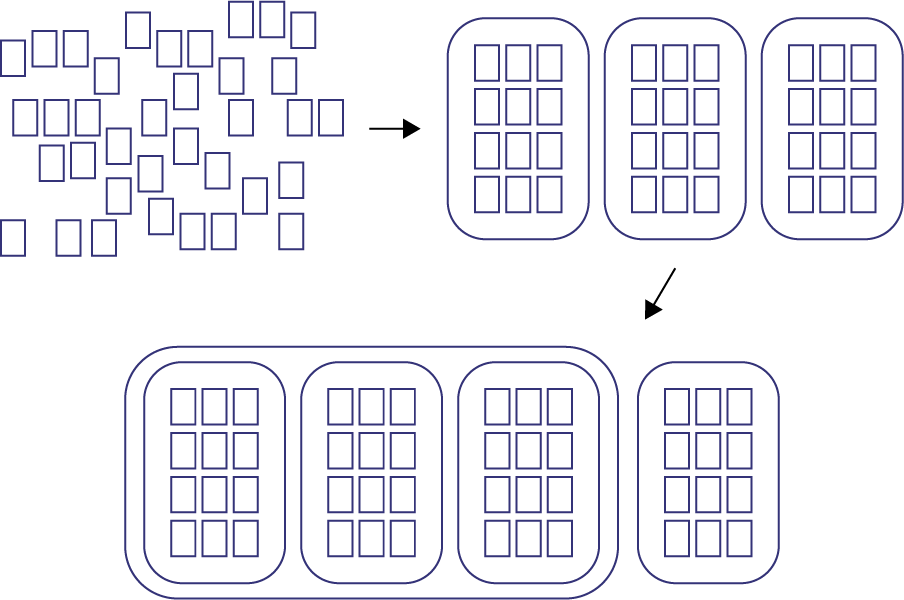

Situation à partie manquante

Il y a 24 poissons dans un aquarium, dont les $\frac{3}{4}$ sont rouges. Combien y a-t-il de poissons rouges dans l'aquarium? (18 poissons)

Représentation de la situation

image Les poissons rouges sont représentés par des jetons rouges. Image un: Un rectangle regroupant 24 jetons rouges dispersés. La pensée de l’élève: “ Mon tout est 24 poissons, que je représente à l’aide de 24 jetons. “Image 2: Un rectangle représentant 24 jetons rouges ordonnés en 4 colonnes de 6 jetons. La pensée de l’élève: “ Puisque je sais que le nombre total de poissons rouges est une fraction de 24, je peux déjà voir que mon résultat sera moins que 24. Je cherche les trois quarts des 24 poissons. Cette fraction peut être représentée par 3 des 4 paquets. Je dois alors séparer les poissons en 4 quarts. Donc, je sépare mes jetons de façon à former 4 paquets équivalents. Il y a 6 jetons dans chaque quart. “Image 3: Un rectangle représentant 4 colonnes de 6 jetons rouges chacune, dont les 3 premières colonnes sont chacune encerclées. La pensée de l’élève: “ Je sélectionne ensuite 3 des 4 paquets. Le contenu représente alors le nombre de poissons rouges dans l’aquarium, soit 18 poissons. “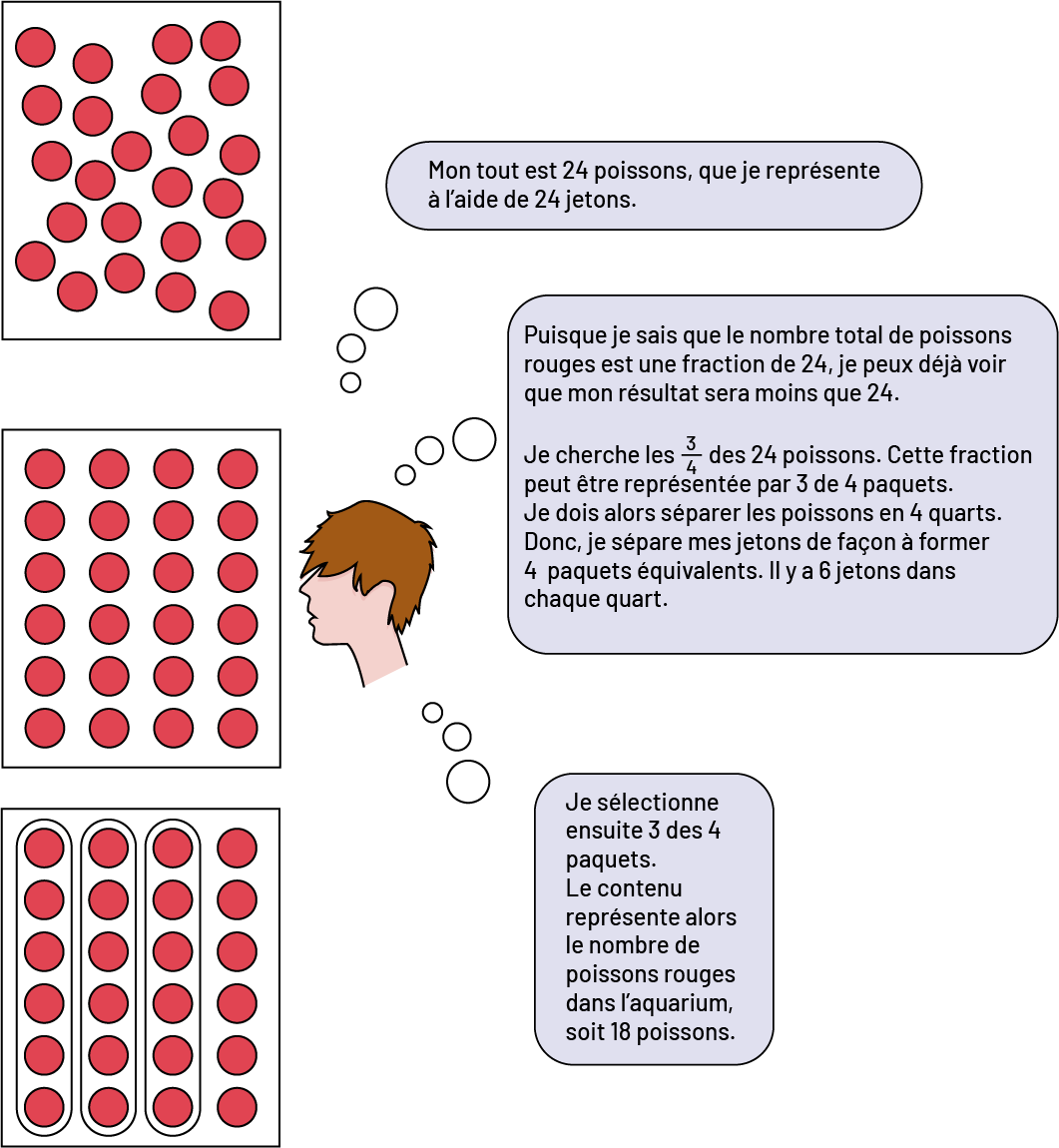

Dans cette dernière situation, en raisonnant de la sorte et en utilisant du matériel concret, les élèves mettent à profit leur compréhension du sens de la fraction et appliquent des stratégies qui découlent de leur compréhension de la fraction comme fraction d’un ensemble. Les élèves peuvent reconnaître que le dénominateur joue un rôle de diviseur (le nombre de parties) et que le numérateur joue un rôle de multiplicateur. Ce type de raisonnement ne s’enseigne pas explicitement, mais il s’acquiert en situation de résolution de problèmes. À la suite de plusieurs expériences, les élèves peuvent généraliser et reconnaître que dans chaque situation, elles et ils divisent le nombre naturel par le dénominateur pour déterminer la grandeur des groupes, et multiplient ensuite cette réponse par le numérateur pour déterminer la quantité dans le nombre de groupes en cause.

En présence d’un modèle d’ensemble et d’une situation à partie manquante, on cherche à déterminer le nombre d’éléments contenus dans cette partie. De fait, on calcule la fraction d’un ensemble. Par exemple, dans la situation précédente, l’élève devait calculer $\frac{3}{4}$ de 24. Ce type de calcul est très important puisqu’il fait partie d’applications du quotidien. En début d’apprentissage, il est important d’explorer des situations dont le résultat est un nombre naturel (par exemple, $\frac{1}{3}$ de 18, $\frac{2}{5}$ de 20, $\frac{3}{4}$ de 12). Ces situations permettent aux élèves d’approfondir leur compréhension et d’acquérir un certain savoir-faire. On peut ensuite explorer des situations dont le résultat est un nombre fractionnaire. Afin de résoudre ce genre de situations, plusieurs stratégies s’offrent aux élèves.

Exemple

Déterminer $\frac{2}{3}$ de 7 biscuits.

Le dénominateur indique le nombre de groupes à créer, en l’occurrence 3 groupes équivalents. On peut facilement placer 6 des biscuits dans les 3 groupes. Le 7^e biscuit devra être coupé en 3 parties équivalentes.

Dans chaque groupe, il y a $2\frac{1}{3}$ biscuits.

Le numérateur d’une fraction indique le nombre de groupes ou de parties considérés. Ainsi, puisqu’on recherche $\frac{2}{3}$ des 7 biscuits, on choisit 2 des 3 groupes.

On peut donc conclure que $\frac{2}{3}$ de 7 biscuits, c’est $4\frac{2}{3}$ biscuits. Afin d’établir le $\frac{2}{3}$ d’un ensemble de 7 objets ($\frac{2}{3}$ de 7), on peut aussi concevoir qu’il s’agit de la somme des $\frac{2}{3}$ de chaque élément de l’ensemble :

($\frac{2}{3}\mathrm{d}\mathrm{e}1+\frac{2}{3}\mathrm{d}\mathrm{e}1+\frac{2}{3}\mathrm{d}\mathrm{e}1+\frac{2}{3}\mathrm{d}\mathrm{e}1+\frac{2}{3}\mathrm{d}\mathrm{e}1+\frac{2}{3}\mathrm{d}\mathrm{e}1+\frac{2}{3}\mathrm{d}\mathrm{e}1$). Ainsi, on obtient $\frac{14}{3}$. En regroupant les tiers, on obtient $4\frac{2}{3}$.

Note : Déterminer la fraction d’un ensemble (par exemple, $\frac{3}{4}$ de 12) peut s’apparenter à une multiplication par une fraction (par exemple, $\frac{3}{4}\times 12$). Cependant, au cycle moyen, il est préférable de miser sur le fait que les élèves cherchent à déterminer une fraction d’un ensemble ($\frac{3}{4}$ de 12), plutôt qu’à effectuer une opération ($\frac{3}{4}\times 12$).

Représentations à l’aide de mots

Il ne faut pas négliger le rôle des mots dans la représentation des fractions. Lorsqu’on parle de trois quarts, le terme « trois » nous dit combien il y a de parties et le terme « quarts » nous renseigne sur la grandeur des parties ou le nombre de parties qui forment un tout. Les mots sont aussi utilisés pour expliquer un raisonnement relié aux fractions, par exemple : « J’ai partagé mes billes en six groupes égaux que je remets à six amis. Chaque ami reçoit alors un des six groupes ou un sixième de mes billes. »

Représentations symboliques

Il va de soi qu’une fraction est aussi représentée de façon symbolique. Rappelons que la fraction exprime une relation entre deux quantités, soit le nombre de parties équivalentes en question (le numérateur) et le nombre de parties qui forment un tout (le dénominateur). Cette relation est exprimée de façon symbolique par une barre de fraction placée entre les deux nombres. Bien que la barre oblique soit souvent utilisée dans la vie de tous les jours (par exemple, 2/3 de rabais), l’utilisation de la barre horizontale est préconisée pour éviter des ambiguïtés (par exemple, une lecture rapide de 2/3 pourrait donner 213; 1 1/3 ressemble à onze tiers).

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 62-71.

Difficultés encourues par les élèves

Une fraction est une partie d’un tout. De façon plus abstraite, une fraction est aussi un nombre (par exemple, le nombre $\frac{1}{2}$ représente la moitié du nombre 1). Elle représente donc une quantité. Cependant, cette quantité n’est pas composée seulement de valeurs entières (par exemple, une quantité de poires peut correspondre à $\frac{1}{2}$ poire, une distance peut être de $1\frac{3}{4}$ km, c’est-à-dire 1 km et une partie d’un autre). Les fractions offrent donc une précision supplémentaire que les nombres naturels ne peuvent donner.

Le développement du sens du nombre relié aux fractions représente un grand défi pour les élèves. Baroody et Coslick (1998, p. 9-13 et 9-14) tentent une explication et soulèvent certaines difficultés tant dans l’apprentissage que dans l’enseignement des fractions. Voici quelques-unes de ces difficultés.

• Les élèves ont du mal à se représenter des fractions selon divers modèles. Puisque l’enseignement des fractions se fait souvent à l’aide d’un seul modèle, par exemple en prenant un cercle ou une tarte, beaucoup d’élèves n’ont pas intégré le fait que pour obtenir une fraction, soit une partie d’un tout, il faut d’abord diviser ce tout en parties équivalentes.

image Une série de 3 images barrées par un X. Les 3 images sont un cercle, un triangle et un rectangle étant chacun divisés en parties non égales et ayant une partie colorée. La 4e image représente un carré divisé en 4 parties égales dont l’une est colorée. La 5e image représente des jetons séparés dans des ensembles de 2 jetons chacun.

• Certains élèves comparent la partie d’un tout à la partie restante plutôt qu’au tout. Dans l’exemple qui suit, $\frac{5}{8}$ de l’ensemble des billes sont rouges. Mais, certains élèves représentent cette situation par la fraction $\frac{5}{3}$.

• Les élèves ne développent pas un solide sens de la fraction puisque souvent, elles et ils ne voient pas le lien entre une fraction (par exemple, $\frac{3}{4}$) et la fraction unitaire correspondante ($\frac{1}{4}$), soit que $\frac{3}{4}=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$ ou que $\frac{3}{4}=3\times \frac{1}{4}$.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 29-30.

Habileté : expliquer la signification du numérateur et du dénominateur

---

La notation fractionnaire $\frac{a}{b}$ est généralement associée au concept de partie d’un tout. Le tout peut être un élément ou un ensemble d’éléments.

Exemple

• J’ai donné un quart ($\frac{1}{4}$) de mon sandwich à Alex.

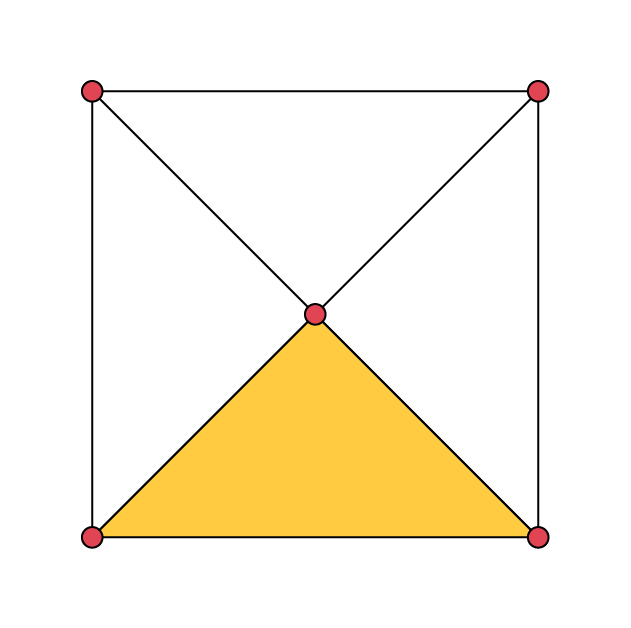
• Un quart ($\frac{1}{4}$) de mes billes sont bleues.

Or, la notation fractionnaire peut être aussi associée à d’autres concepts tels que la division, le rapport et l’opérateur.

Division

Avec le développement de l’algèbre, une division est parfois exprimée sous forme fractionnaire. Prenons, par exemple, une division comme 2 ÷ 3 exprimée ainsi : $\frac{2}{3}$. Dans un tel contexte, on lit « deux divisé par trois » et non pas « deux tiers », ce qui complique les choses. Or, il y a tout de même un lien entre $\frac{2}{3}$ (deux divisé par trois) et $\frac{2}{3}$ (deux tiers). Comme les deux exemples suivants l’expliquent, la réponse de la division de 2 par 3 (2 ÷ 3) est $\frac{2}{3}$ (deux tiers).

Exemple

Trois amis veulent se partager deux pizzas. Combien chacun recevra-t-il? Il s’agit bien de 2 ÷ 3 qui peut être représenté par $\frac{2}{3}$. Pour trouver la réponse, on peut imaginer que la première pizza sera coupée en tiers et chacun recevra un tiers de la pizza. Ensuite, la deuxième pizza sera aussi coupée en tiers et chacun recevra un autre tiers de pizza.

image Des pizzas représentées par des cercles.2 cercles côte à côte divisés en 3 parties égales de coulLeeur jaune, mauve et rouge.Une flèche partant de cette direction et pointant 3 autres cercles chacun divisé en 3 parties égales. Le premier cercle a 2 parties sur 3 qui sont jaunes. Le 2e cercle a 2 parties sur 3 qui sont rouges. Le 3e cercle a 2 parties sur 3 qui sont mauves.

Chaque ami recevra donc deux tiers ($\frac{2}{3}$) d’une pizza.

Rapport

Les rapports peuvent aussi être écrits sous forme de fraction. Un rapport est une comparaison entre deux quantités de même nature au moyen de la division. De façon plus précise, le rapport est le quotient de cette division. Par exemple, s’il y a 2 garçons et 3 filles dans un groupe, on dit que le rapport du nombre de garçons au nombre de filles est de 2 à 3. Ce rapport s’écrit 2 : 3 ou $\frac{2}{3}$ et se lit « 2 à 3 ». Dans ce cas, il s’agit d’un rapport d’une partie d’un ensemble à une autre partie du même ensemble (rapport de partie à partie).

De cette même situation, on peut aussi dire que dans un ensemble de 5 enfants, il y a 2 garçons et 3 filles. Ainsi, on peut dire que le rapport du nombre de garçons au nombre d’enfants est de 2 à 5 (2 : 5). Dans ce cas, il s’agit d’un rapport d’une partie d’un ensemble à l’ensemble (rapport de partie à tout). Le rapport compare une partie à un tout, il s’agit donc d’une fraction. On peut donc aussi dire $\frac{2}{5}$ des enfants de l’ensemble sont des garçons.

Opérateur

Au cycle intermédiaire, la fraction est aussi présentée comme un opérateur dans les situations impliquant la multiplication d’un nombre par une fraction. Par exemple, si 24 morceaux de gomme entrent dans une empaqueteuse qui fait ressortir 12 paquets, il s’agit de $\frac{1}{2}\times 24=12$ qui a été effectué. Dans ce cas, $\frac{1}{2}$ ne représente pas une partie d’un tout (par exemple, $\frac{1}{2}$ gomme), mais une quantité qui opère sur l’ensemble des 24 morceaux de gomme.

Les fractions sont utilisées à diverses fins, peuvent décrire différentes situations, et peuvent avoir des représentations très différentes pour la même fraction.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 36-37.

Connaissance : fraction

---

Le mot fraction vient du latin fractio qui veut dire « rupture ». Une partie d’un objet brisé peut donc représenter une fraction, car c’est une partie d’un tout. Toutefois, pour déterminer une fraction d’un objet divisé en plusieurs parties, il faut que les parties soient équivalentes. Précisons que lorsqu’il est question de parties équivalentes, il ne s’agit pas nécessairement de formes identiques, bien que celles-ci soient plus faciles à utiliser. Les représentations de un quart ($\frac{1}{4}$) dans l’exemple ci-dessous sont basées sur l’aire du tout. Puisque chaque tout a une aire de 16 unités carrées, chaque quart ($\frac{1}{4}$) a une aire de 4 unités carrées. Malgré leurs formes différentes, chacun de ces quarts représente une partie équivalente d’un même tout.

Exemple 
Six représentations équivalentes de un quart ($\frac{1}{4}$) du même tout.

Il est important pour les élèves de comprendre que plus le tout est fractionné, plus ses parties sont petites.

Exemple

Les quarts d’un tout sont plus gros que les dixièmes du même tout.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 33.

Connaissance : notation fractionnaire

---

Nous appelons la fraction écrite $\frac{a}{b}$ la notation fractionnaire. La notation fractionnaire $\frac{a}{b}$ est généralement associée au concept de partie d’un tout. Le tout peut être un élément ou un ensemble d’éléments.

Or, la notation fractionnaire peut être aussi associée à d’autres concepts tels que la division, le rapport et l’opérateur.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 36.

Connaissance : numérateur

---

Nombre de parties équivalentes du tout dont se compose la fraction.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 34.

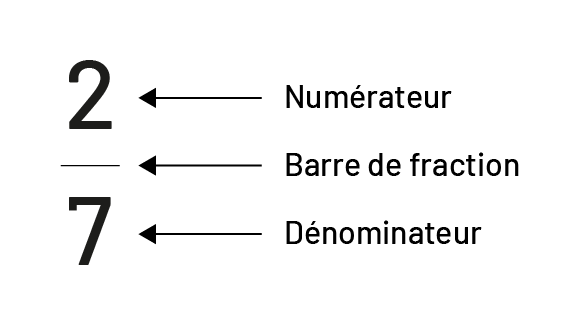
Le numérateur est le nombre au-dessus de la barre de fraction.

image La fraction 2 sur 7 est représentée par le chiffre 2, une barre sous le chiffre 2 et le chiffre 7 sous cette barre. Le chiffre 2 est pointé par une flèche indiquant que c’est le numérateur. La barre sous le 2 est pointée par une flèche indiquant que c’est la barre de fraction. Le chiffre 7 sous la barre est pointée par une flèche indiquant que c’est le dénominateur.

Connaissance : dénominateur

---

Nombre de parties équivalentes par lequel le tout est divisé.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 34.

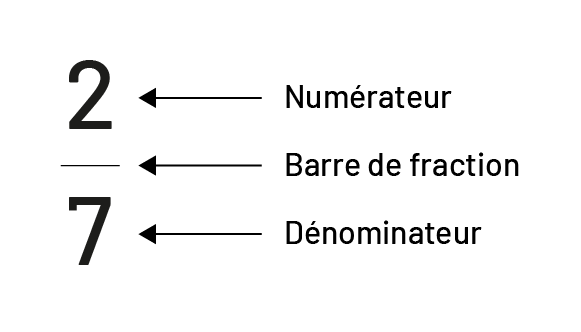
Le dénominateur est le nombre en-dessous de la barre de fraction.

image La fraction 2 sur 7 est représentée par le chiffre 2, une barre sous le chiffre 2 et le chiffre 7 sous cette barre. Le chiffre 2 est pointé par une flèche indiquant que c’est le numérateur. La barre sous le 2 est pointée par une flèche indiquant que c’est la barre de fraction. Le chiffre 7 sous la barre est pointée par une flèche indiquant que c’est le dénominateur.