B1.4 Represent fractions from halves to tenths using drawings, tools, and standard fractional notation, and explain the meanings of the denominator and the numerator.
Skill: Representing Fractions from Halves to Tenths Using Diagrams, Tools and Standard Fractional Notation
Representations Using Models
At the root of students' difficulties with fractions, we too often find the lack of importance given to concrete and visual (semi-concrete) models. The use of models is essential to learning and understanding fractions and should continue throughout the school career. However, among the models used in schools, the circle model is overused and often inappropriate in certain contexts. Teachers must therefore ensure that students learn to represent fractions in various ways depending on the context. In general, we refer to three models, the area model, the linear model and the set model, each of which can take on different appearances depending on the tools and materials used.
Area Model
In this model, an area or region is divided into equal parts. In the classroom, circular models (pie or pizza) and rectangular models can be reproduced on stiff cardboard, then cut and laminated for use in different exercises. Pattern blocks, geoboards, dot paper and grid paper are also good tools that may be more appropriate for particular situations. With these materials, students should be encouraged to fold, layer, split and cut to develop their fraction sense.

The following are examples of situations that can be represented using an area model.
Find the Fraction
Jared cuts a pizza into 6 equal pieces. He eats 2 pieces. What fraction of the pizza did Jared eat? \(\frac{2}{6}\)
Representation of the situation
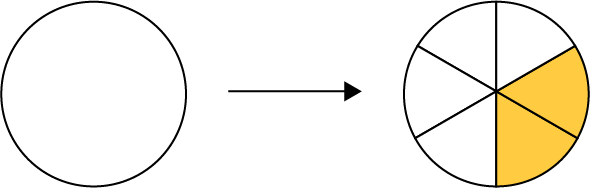
Find the Part
Colour \(\frac{3}{8}\) of the rectangle.

Representation of the situation

Find the Whole
Here is \(\frac{2}{8}\) of a rectangle.

Draw the whole rectangle.
Representation of the situation

Linear Model
In situations involving distance or time, linear models are more appropriate for representing fractions (for example, rulers, cardboard or paper strips, string, line segment).

The following are examples of situations that can be represented using a linear model.
Find the Fraction
During a 15 km marathon, Carlos had to withdraw from the race at the sixth kilometre because of a cramp. What fraction of the marathon had he completed? \(\frac{2}{5}\) of the marathon
Representation of the situation

Find the Part
Michael cut \(\frac{2}{5}\) of a 10 m piece of rope. How long is his end of the rope? (4 m)
Representation of the situation

Find the Whole
Here is \(\frac{2}{3}\) of a line segment.

Draw the complete segment.
Representation of the situation

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 62-65.
Set Model
Using a set model requires a good conceptual understanding of the whole, since the whole is not an element, but a set of elements (for example, 12 objects). Students have difficulty understanding this concept and often only have a superficial grasp of it. For a set of 9 red and 6 green chips, for example, students immediately recognize that \(\frac{9}{{15}}\) of the chips are red, but have difficulty recognizing that \(\frac{3}{5}\) of the chips are red unless they are presented with the chips arranged in groups of 3. In order to understand the set model, it is essential that students have the opportunity to use concrete materials that they can share equally.
The following are examples of situations that can be represented using a set model.

Find the Fraction
Here is a set of marbles. What fraction of the set is yellow? (\(\frac{8}{12}\) of the marbles are yellow.)

Representation of the situation
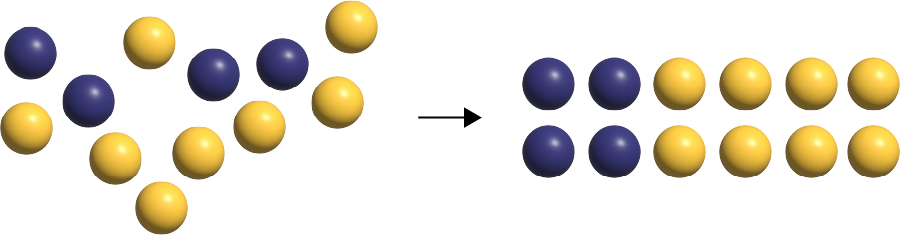
Note: \(\frac{8}{{12}}\) and \(\frac{2}{3}\) would also be acceptable fractions since they are equivalent. Students should determine theses fractions not by applying an algorithm related to the equivalent fractions, but by representing fair sharing of the objects in the set using concrete materials.
Find the Whole
Laurence collects celebrity cards. To date, Laurence has accumulated 36 cards, or \(\frac{3}{4}\) of the cards in the Our Favorite Celebrities set. How many cards are in the set? (48 cards)
Representation of the situation
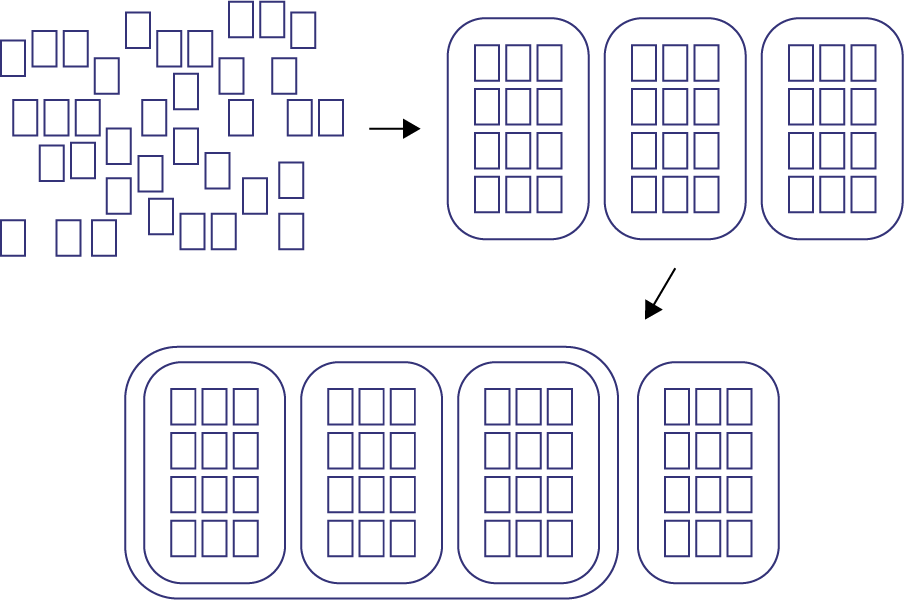
Find the Part
There are 24 fish in an aquarium, \(\frac{3}{4}\) of which are red. How many red fish are in the aquarium? (18 fish)
Representation of the situation
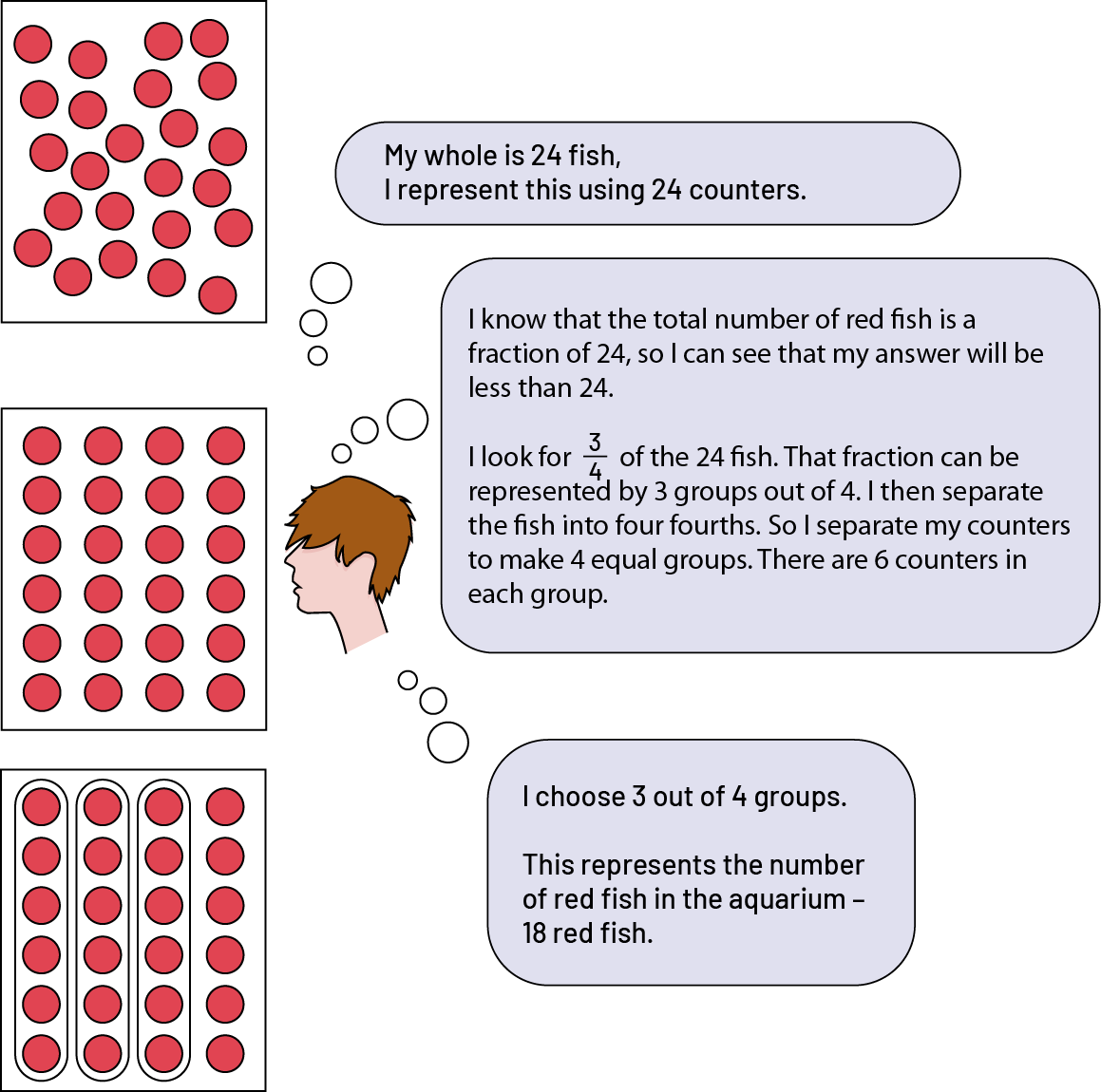
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 66-67.
In the latter situation, by reasoning in this way and using concrete materials, students build on their understanding of the meaning of the fraction and apply strategies that flow from their understanding of the fraction as a part of a whole. Students can recognize that the denominator acts as a divisor (the number of equal parts in a whole) and the numerator acts as a multiplier. This type of reasoning is not explicitly taught, but is learned in problem-solving situations. Through several investigations, students can generalize and recognize that in each situation, they divide the whole number by the denominator to determine the size of the groups, and then multiply that answer by the numerator to determine the quantity in the number of groups involved.
In the situation of a set model with an unknown part, we try to determine the number of elements contained in this unknown part. In effect, we are calculating the value of that part of the set. For example, in the previous situation, there were 24 fish and the student had to calculate how many red fish there were if \(\frac{3}{4}\) of the fish were red. This type of calculation is very important because it is often used in everyday applications. At the beginning of learning about the set model, it is important that students explore situations where the result is a whole number (for example, \(\frac{1}{3}\) of 18, \(\frac{2}{5}\) of 20, \(\frac{3}{4}\) of 12). These situations allow students to deepen their understanding and acquire skills for working with fractions. The next step is to explore situations where the unknown is a fraction. There are several strategies for solving these situations.
Example
Determine \(\frac{2}{3}\) of 7 cookies.

The denominator indicates the number of equal groups to create, in this case 3 equal groups. We can easily place 6 of the cookies in the 3 groups. The 7th cookie will have to be cut into 3 equivalent parts.

In each group, there are \(2\frac{1}{3}\) cookies.

The numerator of a fraction indicates the number of equal groups or parts considered. Thus, since we are looking for \(\frac{2}{3}\) of the 7 cookies, we count the number of cookies in 2 of the 3 groups.

So we can conclude that \(\frac{2}{3}\) of 7 cookies is \(4\frac{2}{3}\) cookies. In order to establish the that \(\frac{2}{3}\) of a set of 7 objects (\(\frac{2}{3}\) of 7), we can also think of it as the sum of 2/3 of each element of the set: (\(\frac{2}{3}\;{ + }\;\frac{2}{3}\;{ + }\;\frac{2}{3}\;{ + }\;\frac{2}{3}\;{ + }\;\frac{2}{3}\;{ + }\;\frac{2}{3}\;{ + }\;\frac{2}{3}\)). So we have \(\frac{{14}}{3}\). When we combine the thirds, we get \(4\frac{2}{3}\).
Note: Determining a fraction of a set (for example, \(\frac{3}{4}\) of 12) can be similar to multiplying by a fraction (for example,\(\frac{3}{4}\; \times \;12\)). However, in the junior grades, it is best to focus on students trying to determine the value of a fraction of a set (\(\frac{3}{4}\) of 12), rather than performing an operation (\(\frac{3}{4}\; \times \;12\)).
Representations Using Words
The importance of words in representing fractions should not be overlooked. When we talk about three fourths, the word "three" tells us how many equal parts are being counted and the word "fourths" tells us how many equal parts make up a whole. The words are also used to explain a reasoning related to fractions, for example: "I divided my marbles into six equal groups and gave them to six friends. Each friend received one of the six groups or one sixth of my marbles.
Symbolic Representations
It goes without saying that a fraction is also represented symbolically. Recall that a fraction expresses a relationship between two quantities, namely the number of equal parts in question (the numerator) and the number of equal parts that form a whole (the denominator). This relationship is expressed symbolically by a slash between the two numbers. Although the slash is often used in everyday life (for example, 2/3 off), the use of the horizontal line is advocated to avoid ambiguity (for example, a quick reading of 2/3 might yield 213; 1 1/3 looks like eleven thirds).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 62-71.
Difficulties Encountered by Students
A fraction is a part of a whole. More abstractly, a fraction is also a number (for example, the number \(\frac{1}{2}\) represents half of the number 1). It therefore represents a quantity. However, this quantity is not composed only of whole number values (for example, a quantity of pears may be \(\frac{1}{2}\) a pear, a distance may be \(1\frac{3}{4}\) km, that is, 1 km and a part of another). Fractions thus offer an additional precision that whole numbers cannot give.
Developing number sense related to fractions is a great challenge for students. Baroody and Coslick (1998, pp. 9-13 and 9-14) attempt an explanation and raise some difficulties in both learning and teaching fractions. The following are some of these difficulties.
- Students have difficulty picturing fractions in a variety of models. Since fractions are often taught using a single model, such as a circle or a pie, many students have not integrated the fact that in order to get a fraction, which is a part of a whole, one must first divide the whole into equal parts.

- Some students compare the part of a whole to the remaining part rather than the whole. In the following example, 5/8 of the marbles are red. But, some students represent this situation with the fraction 5/3.

- Students do not develop a strong sense of fraction since they often do not see the connection between a fraction (for example, \(\frac{3}{4}\) and the corresponding unit fraction \(\frac{1}{4}\), either \(\frac{3}{4}\) = \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) or that \(\frac{3}{4} = 3 \times \frac{1}{4}\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 29-30.
Skill: Explaining the Meaning of the Numerator and the Denominator
Fractional notation \(\frac{a}{b}\) is generally associated with the concept of a part of a whole. The whole can be an element or a set of elements.
Example
- I gave fourth (\(\frac{1}{4}\)) of my sandwich to Alex.
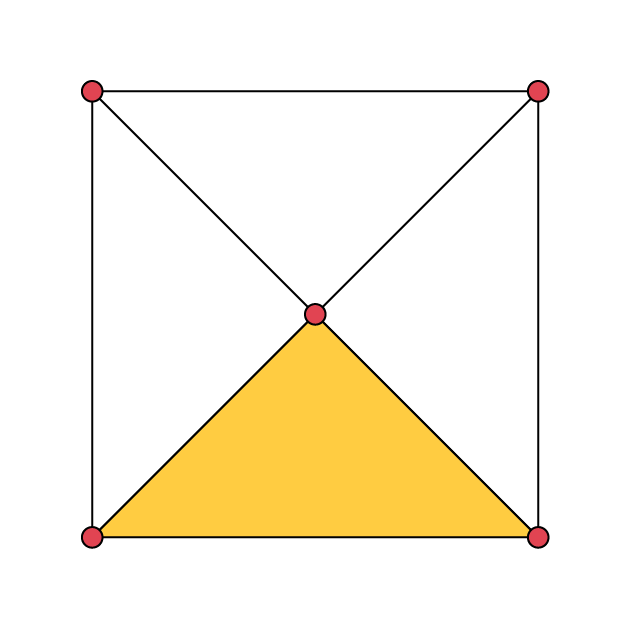
- One fourth (\(\frac{1}{4}\)) of my marbles are blue.

However, fractional notation can also be associated with other concepts such as division, a comparison and operator.
Division
With the development of algebra skills, a division is sometimes expressed in fractional form. For example, a division such as 2 ÷ 3 can be expressed as: \(\frac{2}{3}\). In this context, we read "two divided by three" and not "two thirds", which in itself can be mysterious. However, there is a connection between \(\frac{2}{3}\)(two divided by three) and \(\frac{2}{3}\) (two thirds). As the following two examples illustrate, the answer to dividing 2 by 3 (2 ÷ 3) is \(\frac{2}{3}\) (two thirds).
Example
Three friends want to share two pizzas. How much will each get? The answer is 2 ÷ 3, which can be represented by \(\frac{2}{3}\). To find the answer, we can imagine that the first pizza will be cut into thirds and each will receive one third of the pizza. Then the second pizza will also be cut into thirds and each person will receive one third of that pizza.

Each friend will receive two thirds of a pizza.
Comparisons
Fractions can also represent a comparison and show the relationship between two parts of the same whole. The numerator is one part and the denominator is the other part. For example, if there are 2 red beads and 3 yellow beads in a bag, the fraction \(\frac{2}{3}\) represents that there are two thirds as many red beads as yellow beads.
Operator
In the intermediate grades, the fraction is also introduced as an operator in situations involving the multiplication of a number by a fraction. For example, if 24 pieces of gum go into a packaging machine that produces 12 packages, then the 24 has been halved, which can be represented by multiplying by the fraction one half or \(\frac{1}{2}\; \times \;24\; = \;12\). In this case, \(\frac{1}{2}\) does not represent a part of a whole (half of the gum), but a quantity that operates on all 24 pieces of gum.
Fractions are used for different purposes, can describe different situations, and can have very different representations.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 36-37.
Knowledge: Fractions
The word fraction comes from the Latin fractio which means "break". In order to determine a fraction of a whole that has been broken or divided into parts, the parts must be equal sizes. Note that when we talk about equal parts, we are not necessarily talking about identical shapes, although these are easier to use. The representations of one fourth (\(\frac{1}{4}\)) in the example below are based on the area of the whole. Since each whole has an area of 16 square units, each fourth (\(\frac{1}{4}\)) has an area of 4 square units. Despite their different shapes, each of these fourths represents an equal part of the same whole.
Example
Six equivalent representations of one fourth (\(\frac{1}{4}\)) of the same whole.

It is important for students to understand that the more the whole is divided, the smaller the parts.
Example
Fourths of a whole are bigger than tenths of the same whole.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 33.
Knowledge: Fractional Notation
We refer to the fraction written \(\frac{a}{b}\) as fractional notation . Fractional notation \(\frac{a}{b}\)s is usually associated with the understanding of fractions as parts of a whole. The whole can be an element or a set of elements.
However, fractional notation can also be associated with other concepts such as division, comparison and operator.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 36.
Knowledge: Numerator
Number of equal parts of the whole being considered.
Source: gtranslated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 34.
The numerator is the number above the line in a fraction.
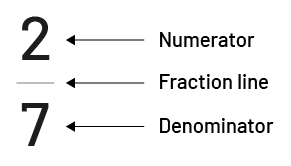
Knowledge: Denominator
Number of equal parts by which the whole is divided.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 34.
The denominator is the number below the fraction bar.

