B2.5 Représenter et résoudre des problèmes relatifs à la multiplication d’un nombre naturel à deux ou à trois chiffres par un nombre naturel à un chiffre, et par 10, 100, et 1 000, à l’aide d’outils appropriés, y compris des dispositions rectangulaires.
Habileté : résoudre des problèmes de multiplication d’un nombre naturel à deux ou trois chiffres par un nombre naturel à un chiffre
Lors de la résolution de problèmes, on encourage les élèves à utiliser les connaissances déjà acquises et à établir des liens avec le nouvel apprentissage. Ces liens peuvent être rompus si on ne présente pas aux élèves un éventail diversifié de problèmes. Les élèves qui n’apprennent pas à calculer dans des contextes de résolution de problèmes pourraient avoir beaucoup de difficulté à faire ces liens plus tard. Leur compréhension de la notion abstraite du nombre et de son application risque d’être floue, et il est possible que certains n’arrivent pas à utiliser efficacement des stratégies de calcul pour résoudre des problèmes.
Le recours à des contextes de résolution de problèmes est tout aussi important pour les opérations sur les nombres à plusieurs chiffres. Lorsqu’on donne des problèmes aux élèves, lorsqu’on les encourage à trouver un algorithme et à l’utiliser de manière souple, on leur donne l’occasion d’approfondir leur compréhension des opérations. Par souci d’efficacité et croyant bien faire, on enseigne souvent aux élèves l’algorithme à utiliser pour effectuer les opérations sur les nombres à plusieurs chiffres. Cette méthode leur étant présentée comme la « bonne façon » de résoudre le problème, les élèves font des efforts ardus pour comprendre et mémoriser cette procédure. Cette méthode entraîne souvent une utilisation peu efficace de l’algorithme, un manque d’exactitude et une compréhension limitée. Si, au contraire, on encourage les élèves à dégager le sens du problème et à élaborer leurs propres stratégies pour le résoudre, elles et ils démontreront plus d’aisance et plus de précision dans leur travail sur les opérations.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 5.
Types de problèmes relatifs à la multiplication
Les élèves acquièrent une bonne compréhension de la multiplication et des relations entre les nombres en résolvant des problèmes de différents types.
Les types de problèmes présentés ci-après à l’aide d’exemples peuvent aider les élèves à percevoir les opérations relatives à la multiplication et division de diverses façons, selon qu’il s’agit de problèmes de groupes égaux, de comparaison ou de combinaisons. Le recours à ces différents types de problèmes oblige les élèves à raisonner pour trouver des solutions et permet ainsi de développer un meilleur sens des opérations.
Les exemples de problèmes écrits ci-dessous contiennent des nombres à deux ou trois chiffres fois un nombre d’un chiffre. Les structures des trois types de problèmes écrits se prêtent aussi aux nombres à plusieurs chiffres.
Problème de groupes égaux
L’École a acheté 150 livres pour les classes. Chacun a coûté 5 $. Combien l’école a-t-elle dépensé pour tous ces livres?
\[150 \times 5\;\$ = ?\]
Décomposition du premier terme et la distributivité
\(\begin{array}{l}150 \times 5\;\$ &= (100 \times 5) + (50 \times 5)\\\quad \quad \quad \;{\kern 1pt} &= 500 + 250\\\quad \quad \quad \;{\kern 1pt} {\kern 1pt} &= 750\;\$ \end{array}\)
L’école a dépensé 750 $ pour tous ces livres.
Problème de comparaison en multiplication
La représentation de la situation avec les réglettes Cuisenaire ou la droite numérique aide à déterminer le résultat.
- Comparaison : produit inconnu
Mustapha a épargné 20$ au cours du dernier mois. Pour sa part, Michel en a épargné 4 fois plus. Combien d’argent Michel a-t-il épargné?
\[4 \times 20\;\$ = ?\]
Addition répétée à l’aide de réglettes Cuisenaire
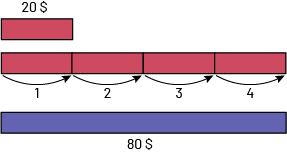image Une
petite réglette rouge représentant 20 dollars.En dessous il y a 4 petites réglettes rouges collées les unes à la suite
des autres et chacune ayant une flèche partant de sa direction et allant vers la réglette à sa droite indiquant que
l’on passe de, une à 4 réglettes.Dessous il y a une grosse réglette mauve aussi longue que les 4 réglettes rouges du
dessus. Cette réglette est intitulée: 80 dollars.
\(\begin{array}{l}4 \times 20\;\$ &= 20 + 20 + 20 + 20\\\quad \quad &= 80\;\$ \end{array}\)
Michel a épargné 80 $.
Problème de combinaison
- Combinaison : produit inconnu
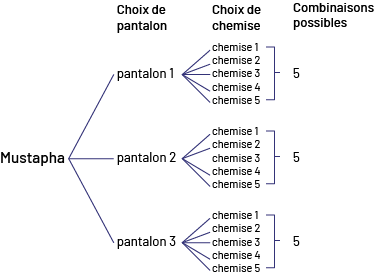
Mustapha a 3 pantalons et 5 chemises. Combien de tenues différentes Mustapha a-t-il?
Diagramme en arbre
image
Diagramme en arbre de Mustapha.De gauche à droite, les branches sont:Choix de pantalon, choix de chemise et
combinaisons possibles.Sous la branche pantalon, il y a 3 possibilités: pantalon un, pantalon 2 ou pantalon 3.Sous la
branche choix de chemise, i y a 5 choix possibles pour chaque choix de pantalon soit:Chemise un, chemise 2, chemise 3,
chemise 4 et chemise 5.Sous la branche combinaisons possibles, un crochet réunion les 5 choix de chemises pour chaque
choix de pantalons indiquant qu’il y a 5 combinaisons possibles par choix de pantalon.5 plus 5 plus 5 égal 15 ou 3
fois 5 égal 15.
\(5 + 5 + 5 = 15\quad \;\;{\rm{ou}} \;\; \quad 3 \times 5 = 15\)
Mustapha a 15 tenues différentes.
Source : adapté de Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10-11.
Au début de l’apprentissage de la multiplication, les élèves reconnaissent que la situation présente « plusieurs fois » une même quantité et elles et ils utilisent des groupes égaux pour représenter la situation et l’addition répétée pour obtenir la réponse. À mesure que les élèves progressent, il est important qu’elles et ils y voient le concept de multiplication plutôt que celui d’addition et qu’elles et ils apprennent d’autres représentations.
La disposition rectangulaire, un agencement de rangées et de colonnes, s’avère un modèle puissant dans l’apprentissage de la multiplication et permet de voir cette opération sous un angle différent.
image Image
un:Trois fois 4Trois groupes de quatre 3 fois 4Image 2:Addition répétée4 Plus 4 plus 4Image 3: Groupes égaux3
ensembles 4 pointsImage 4:Disposition rectangulaireUn bout de papier quadrillé ayant 4 colonnes et de large et 3
lignes de haut. Le chiffre 4 est indiqué au haut du papier et le chiffre 3 est indiqué à droite du papier.
En résolvant une variété de problèmes et en discutant de stratégies, les élèves en viennent à établir et à saisir le lien entre le mot « fois » et le signe « × », étape cruciale dans le développement de la compréhension de la multiplication. Les élèves doivent comprendre que le signe « × » signifie « groupes de ».
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 85-86.
Le modèle de la disposition rectangulaire peut être présenté aux élèves de différentes façons. Dans le cadre d’un échange mathématique, par exemple, le personnel enseignant peut partir du travail d’un élève et proposer une nouvelle organisation des objets en disposition rectangulaire.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 134.
Lorsqu’il s’agit d’une multiplication, on connaît le nombre de rangées et le nombre de colonnes. Pour la division, on connaît le nombre total ainsi que le nombre de rangées ou le nombre de colonnes. Pour organiser les objets dans une disposition rectangulaire, les objets sont placés dans des rangées ou des colonnes connues jusqu’à ce que tous les objets soient distribués de manière égale.
Source : adapté du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemples
- Il y a 4 gros biscuits sur chaque plateau. S’il y a 3 plateaux, combien y a-t-il de biscuits?
image Image
un:Trois fois 4Image 2:Addition répétée4 Plus 4 plus 4Image 3: Groupes égaux3 ensembles 4 biscuitsImage 4:Disposition
rectangulaireUn bout de papier quadrillé ayant 4 colonnes et de large et 3 lignes de haut. Le chiffre 4 est indiqué au
haut du papier et le chiffre 3 est indiqué à droite du papier.
- Douze biscuits ont été cuits. Si chaque plateau contient 4 biscuits, combien de plateaux faut-il?
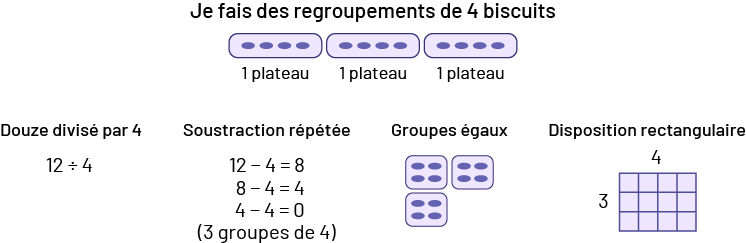image Image
un: Je fais des regroupements de 4 biscuits.On peut voir 3 ensembles de 4 biscuits et l’inscription “ un plateau ” est
écrite sous chaque ensemble.Image 2:Douze divisé par quatre.12 divisé par 4.Image 3:Soustraction répétée12 moins 4
égal 88 moins 4 égal 44 moins 4 égal zéro(Parenthèse ouvrante)3 groupes de 4 (parenthèse fermante)Image 4: Groupes
égaux3 ensembles de 4 biscuitsImage 5:Disposition rectangulaireUn bout de papier quadrillé ayant 4 colonnes et de
large et 3 lignes de haut. Le chiffre 4 est indiqué au haut du papier et le chiffre 3 est indiqué à droite du
papier.
- Douze biscuits ont été cuits. Si 3 plateaux étaient utilisés avec le même nombre de biscuits sur chaque plateau, combien y en avait-il sur chaque plateau?
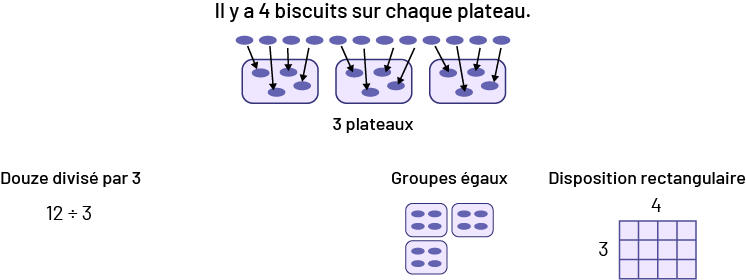image Image
un:Il y a 4 biscuits sur chaque plateauLe dessin monte 12 biscuits individuels. Chaque biscuit est pointé par une
flèche et visant un plateau. Les 4 premiers biscuits pointent vers le premier plateau. Les 4 biscuits suivant pointent
vers le deuxième plateau et les 4 derniers biscuits pointent vers le dernier plateau.Image 2:Douze divisé par 312
divisé par 3 égal 4.Image 3:Groupes égaux3 ensembles de 4 biscuitsImage 4: Disposition rectangulaireUn bout de papier
quadrillé ayant 4 colonnes et de large et 3 lignes de haut. Le chiffre 4 est indiqué au haut du papier et le chiffre 3
est indiqué à droite du papier.
On peut aussi présenter divers articles de la vie courante placés en arrangements rectangulaires (par exemple, boîte à œufs, boîtes de jus, contenants de yogourt, moule à muffins) et demander comment déterminer le nombre d’articles. Certains font un dénombrement, mais plusieurs, intuitivement, effectuent une addition répétée ou même une multiplication en fonction des rangées.
Lorsque les élèves comprennent bien le modèle, il est possible d’utiliser une disposition rectangulaire pour effectuer un calcul. On peut le faire sur du papier quadrillé.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 134-135.
Exemple
Une planche à roulettes a 4 roues. Combien de roues ont 17 planches à roulettes?
\(17 \times 4 = ?\)
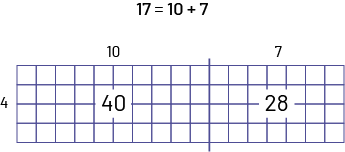
À l’aide de la commutativité, je change la multiplication à \(4\; \times \;17\). Il est plus facile de visualiser 4 rangées de 17 petits carrés. Je décompose 17 en \(10\; + \;7\).
image
Papier quadrillé de 4 rangées de 17 petits carrés.17 égal dix plus 7.4 est inscrit à gauche du papier.Dix est inscrit
au-dessus du papier vis-à-vis des dix premiers carrés et 7 est inscrit au-dessus du papier plus à droite.Le nombre 40
est indiqué au centre des dix premières colonnes.Le nombre 28 est indiqué au centre des 7 dernières colonnes.
\(40 + 28 = 68\)
Il y a 68 roues sur 17 planches à roulettes.
Exemple
À l’école L’Étoile du Nord, il y a 6 classes de 24 élèves. Combien d’élèves y a-t-il en tout?
\[6 \times 24 = ?\]
La distributivité et la disposition rectangulaire
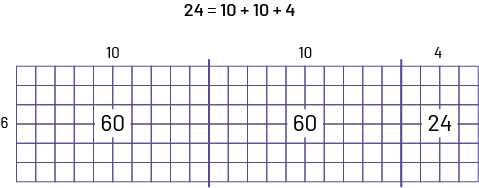
Pour mieux calculer le nombre de carrés, on trace des lignes épaisses afin de délimiter les regroupements de 10 du deuxième facteur.
\(\left( {24\; = \;10\; + \;10\; + \;4} \right)\)
image
24 égal dix plus dix plus 4.Papier quadrillé de 6 rangées de 24 petits carrés.6 est inscrit à gauche du papier.Dix est
inscrit au-dessus du papier vis-à-vis des dix premiers carrés, un autre dix est inscrit au-dessus du papier vis-à-vis
des dix colonnes suivantes et 4 est inscrit au-dessus du papier plus à droite.Le nombre 60 est indiqué au centre des
dix premières colonnes.Le nombre 60 est indiqué au centre des dix colonnes suivantes.Le nombre 24 est indiqué au
centre des 4 dernières colonnes.
\(\begin{array}{l}60 + 60 + 24 &= 120 + 24\\ &= 144\end{array}\)
Il y a 144 élèves en tout.
Cette représentation s’apparente à une disposition rectangulaire créée avec du matériel de base dix.
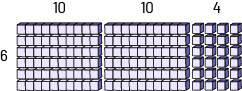image Deux
planchettes de 6 languettes horizontales chacune. Le nombre dix est inscrit au-dessus de chaque planchette.Le nombre 6
est inscrit à gauche des planchettes. Chaque languette équivaut à dix unités.Un ensemble de 24 unités disposé en 4
colonnes de 6 unités chacune.Le chiffre 4 est indiqué au-dessus de cet ensemble.
\(\begin{array}{l}60 + 60 + 24 &= 120 + 24\\ &= 144\end{array}\)
Dans les exemples précédents, toutes les rangées et toutes les colonnes sont délimitées. Donc, chaque unité est identifiable. Avec le temps, les élèves peuvent représenter la même situation autrement en créant des dispositions rectangulaires variées où chaque unité n’est pas représentée. Voici trois autres dispositions rectangulaires qui représentent \(6\; \times \;24\).
image Disposition rectangulaire de 2 colonnes.À gauche du rectangle
le chiffre 6.Au-dessus de la première colonne du rectangle, sont indiquées 2 dizaines. Au-dessus de la deuxième
colonne du rectangle, sont indiquées 4 unités.À l’intérieur du rectangle dans la première colonne se trouve le
résultat de la multiplication de ce qui est écrit à gauche par ce qui est écrit en haut, soit 12 dizaines.Dans la
deuxième colonne du rectangle, il est indiqué 24 unités, soit le résultat de la multiplication de ce qui est écrit
à gauche par ce qui est écrit au-dessus.
\(\begin{align}6 \times 24 &= (6 \times 2\;\;{\rm{dizaines)}} + (6 \times 4\;\;{\rm{unités}})\\ &= 12\;\;{\rm{dizaines}} + 24\;\;{\rm{unités}}\\ &= 12\;\;{\rm{dizaines}} + (2\;\;{\rm{dizaines}} + 4\;\;{\rm{unités}})\\ &= 14\;\;{\rm{dizaines}} + 4\;\;\;{\rm{unités}}\\ &= 144\end{align}\)
image Disposition rectangulaire de 2 colonnes.À gauche du rectangle
le chiffre 6.Au-dessus de la première colonne du rectangle est indiqué 20. Au-dessus de la deuxième colonne du
rectangle est indiqué 4.À l’intérieur du rectangle dans la première colonne se trouve le résultat de la
multiplication de ce qui est écrit à gauche par ce qui est écrit en haut, soit 120.Dans la deuxième colonne du
rectangle, il est indiqué 24, soit le résultat de la multiplication de ce qui est écrit à gauche par ce qui est
écrit au-dessus.
\(\begin{align}6 \times 24 &= (6 \times 20{\rm{)}} + (6 \times 4)\\ &= 120 + 24\\ &= 144\end{align}\)
image Disposition rectangulaire de 3 colonnes.À gauche du rectangle
le chiffre 6.Au-dessus de la première colonne du rectangle est indiqué dix. Au-dessus de la deuxième colonne du
rectangle est indiqué dix. Au-dessus de la troisième colonne est indiqué 4.À l’intérieur du rectangle dans la
première colonne se trouve le résultat de la multiplication de ce qui est écrit à gauche par ce qui est écrit en
haut, soit 60.Dans la deuxième colonne du rectangle, il est indiqué 60, soit le résultat de la multiplication de
ce qui est écrit à gauche par ce qui est écrit au-dessus.Dans la troisième colonne, il est indiqué 24.
\(\begin{align}6 \times 24 &= (6 \times 10{\rm{)}} + (6 \times 10) + (6 \times 4)\\ &= 60 + 60 + 24\\ &= 120 + 24\\ &= 144\end{align}\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 135-136.
Au fur et à mesure que les élèves développent l’habileté à utiliser les dispositions rectangulaires et qu’elles et ils comprennent la stratégie de faire la somme de produits partiels liés au concept d’aire, elles et ils sont en mesure de résoudre des problèmes de multiplication sur des nombres plus grands. Il suffit de décomposer chacun des deux facteurs en fonction des dizaines et des unités. La disposition rectangulaire est encore utile pour représenter la décomposition et les produits partiels comme l’illustre l’exemple suivant :
Il y a 5 manèges à la foire. Chaque manège accommode 27 personnes. Combien peut-il y avoir de personnes dans tous les manèges?
image
Disposition rectangulaire d'une colonne et de 2 lignes.Au-dessus du rectangle est inscrit “ 5 manèges ”.À gauche
vis-à-vis la première ligne est inscrite “ 20 personnes ”.À gauche vis-à-vis la deuxième ligne est inscrite: “7
personnes”.Dans la première case à l’intérieur du rectangle est inscrit:20 fois 5 égal 100.Dans la deuxième case à
l’intérieur du rectangle est inscrit:7 fois 5 égal 35.
Lorsque le nombre 27 est décomposé en 20 et 7, on se trouve à réduire le produit \(5\; \times \;27\) à la somme de deux produits partiels faciles à calculer, soit \(\left( {20\; \times \;5} \right)\; + \;\left( {7\; \times \;5} \right)\), pour un total de 135 personnes.
Le personnel enseignant peut à ce moment proposer aux élèves de noter ces produits partiels dans un tableau de valeur de position comme ci-dessous :
image Tableau de valeur de position, centaines, dizaines, unités, où sont placés les nombres suivants
: 27 multiplié par 5. 7 multiplié par 5 est égal 35.20 multiplié par 5 est égal à 100.100 plus 35 est égal à
135.
L’ordre dans lequel les élèves inscrivent leurs produits partiels dans le tableau n’a pas d’importance. Lorsque les élèves auront maîtrisé l’utilisation d’un tableau de valeur de position pour noter les produits partiels associés à une multiplication quelconque, le personnel enseignant pourra leur présenter l’algorithme usuel de la multiplication. Il importe de mettre en évidence le lien entre les étapes de l’algorithme et celles dans le tableau de valeur de position. Les élèves comprendront alors que l’algorithme usuel de la multiplication n’est qu’une façon rapide de réduire la multiplication à une somme de produits partiels.
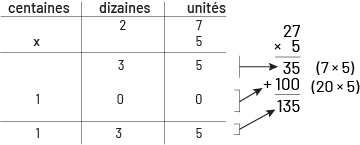image Tableau de valeur de position, centaines, dizaines, unités, où sont placés les nombres suivants
: 27 multiplié par 5. 7 multiplié par 5 est égal 35.20 multiplié par 5 est égal à 100.100 plus 35 est égal à 135.La
multiplication 27 fois 5 est ensuite écrite verticalement.
Source : adapté de Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 63-64.
Connaissance : disposition rectangulaire
La disposition rectangulaire peut être un modèle très utile pour représenter la multiplication et la division puisqu’elle structure des groupes égaux répétés en rangées et en colonnes. Elle établit des liens visuels avec la distributivité, la relation inverse entre la multiplication et la division, ainsi que la mesure de l’aire.
La disposition rectangulaire représente une multiplication associée à l’aire d’un rectangle \(\left( {b\; \times \;h} \right)\). Un produit inconnu est décomposé en produits partiels basés sur des faits connus et des nombres avec lesquels il est plus facile d’effectuer des calculs. Le total des produits partiels est ensuite établi. Les algorithmes usuels pour la multiplication sont fondés sur la distributivité.
Par exemple : \(5\; \times \;78\)
image
Disposition rectangulaireReprésentation.Rectangle divisé en 2 colonnes.Le chiffre 5 désignant la hauteur du rectangle
est indiqué à gauche.Le nombre 70 désignant la largeur de la première colonne est indiqué sous le rectangle.Le chiffre
8 désignant la largeur de la deuxième colonne est indiqué sous le rectangle.Le nombre 78 désigne la largeur intégrale
du rectangle.À l’intérieur de la première colonne:70 fois 5.À l’intérieur de la deuxième colonne: 8 fois 5.
Source : modifié du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année 2020, Ministère de l’Éducation de l’Ontario.
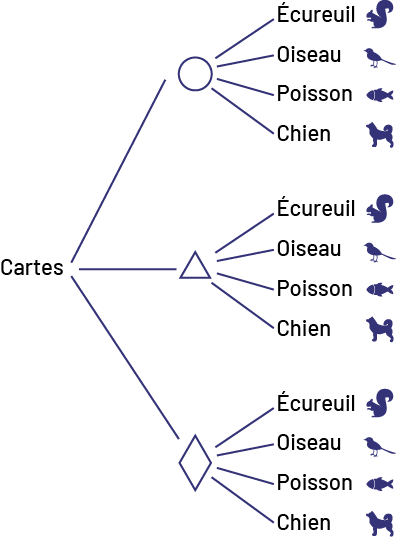
Connaissance : diagramme en arbre
Schéma servant à dénombrer des éléments de façon à mettre en évidence l’ensemble des choix possibles, c’est-à-dire tous les résultats possibles d’un événement ou des événements recherchés.
Exemple
Source : adapté d’UPBALF 6e année, TDP, module 1, p. 215.