B2.5 Represent and solve problems involving the multiplication of two- or three-digit whole numbers by one-digit whole numbers, and by 10, 100, and 1000, using appropriate tools, including arrays.
Skill: Solving Problems Involving Multiplication of Two- or Three-Digit Whole Numbers by One-Digit Whole Numbers
When solving problems, students are encouraged to use knowledge already acquired and to make connections to new learning. These connections can be broken if students are not presented with a diverse range of problems. Students who do not learn to perform calculations within problem-solving contexts may have great difficulty making these connections later. Their understanding of the abstract concept of number and its application may be blurred, and some may not be able to use computational strategies effectively to solve problems.
The use of problem-solving contexts is equally important for multi-digit number operations. When students are given problems, when they are encouraged to come up with an algorithm and use it flexibly, they are given the opportunity to deepen their understanding of operations. In the interest of efficiency and in the belief that they are doing the right thing, students are often taught the algorithm to use to perform operations on multi-digit numbers. Because this method is presented to them as the "right way" to solve the problem, students work hard to understand and remember this procedure. This method often results in inefficient use of the algorithm, lack of accuracy, and limited understanding. If, instead, students are encouraged to make sense of the problem and develop their own strategies for solving it, they will show more fluency and accuracy in their work with operations.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 5.
Types of Multiplication Problems
Students develop an understanding of multiplication and division and the relationships between numbers by solving problems.
The types of problems and examples presented below can support students to see basic number facts about multiplication and division in a variety of ways. Using problems to introduce basic number facts promotes students to reason their way to solutions and thus develops a better sense of operations.
The examples of written problems below contain multiplications of two- and three-digit numbers by one-digit numbers. The structures of all three types of written problems also lend themselves to multi-digit numbers.
Equal Group Problem

The School purchased 150 books for the classes. Each one cost $5. How much did the school spend on all these books?

\(150 \times $ \;5 = ?\)
Decomposition of the First Term and Distributivity
\(\begin{array}{l}150 \times \$\;5 &= (100 \times 5) + (50 \times 5)\\\quad \quad \quad \;{\kern 1pt} &= 500 + 250\\\quad \quad \quad \;{\kern 1pt} {\kern 1pt} &= \$\; 750 \end{array}\)
The school spent $750 on all of these books.
Multiplicative Comparison Problem
Representation of the situation with the relational rods or the number line helps to determine the product.
- Comparison: Product Unknown
Mustapha earns $20 a week for doing chores around the house. How much money does he have after four weeks?
\[4 \times \$\;20 = ?\]
Repeated Addition with Relational Rods
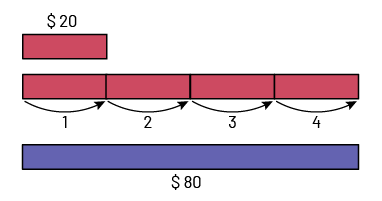
\(\begin{array}{l}4 \times \$\;20 &= 20 + 20 + 20 + 20\\ &= \$\;80 \end{array}\)
Mustapha has $80 after four weeks.
Combinations Problem
- Combination: Product Unknown
Mustapha has 3 pairs of pants and 5 shirts. How many different outfits does Mustapha have?
Tree Diagram
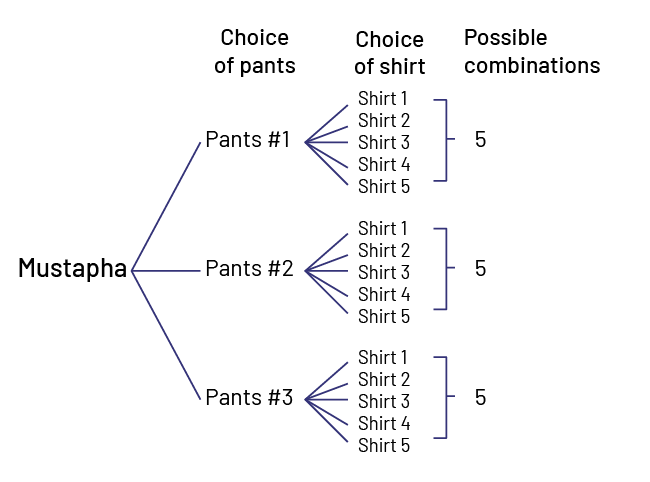
\[5 + 5 + 5 = 15\quad {\rm{or}}\quad 3 \times 5 = 15\]
Mustapha has 15 different outfits.
Source: adapted from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 10-11.
In the early stages of learning multiplication, students recognize that the situation presents the same quantity "many times" and they use equal groups to represent the situation and repeated addition to get the answer. As students progress, it is important that they begin to see multiplication as more than repeated addition and learn other representations.
The array, an arrangement of rows and columns, is a powerful model for learning multiplication and provides a different perspective on the operation.

Through solving a variety of problems and discussing strategies, students come to establish and understand the relationship between the word "times" and the "×" sign, a crucial step in developing an understanding of multiplication. Students need to understand that the "×" sign can mean "groups of".
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 85-86.
The array model can be introduced to students in a variety of ways. For example, teachers can start with a student's work as a starting point and propose organizing objects into an array.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 134.
In a multiplication situation the number of rows and the number of columns for the array are both known. In a division situation the total number of objects is known, as well as either the number of rows or the number of columns. In order to create an array to represent a division situation, the objects are arranged into the rows or columns that are known until all the objects have been distributed evenly.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8 , 2020, Ontario Ministry of Education.
Examples
- There are 4 large cookies on each tray. If there are 3 trays, how many cookies are there?
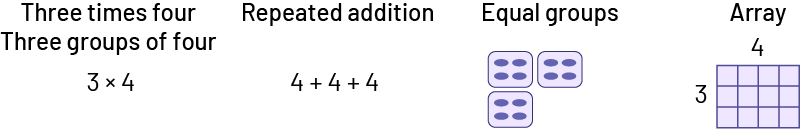
- Twelve cookies have been baked. If each tray contains 4 cookies, how many trays were needed?
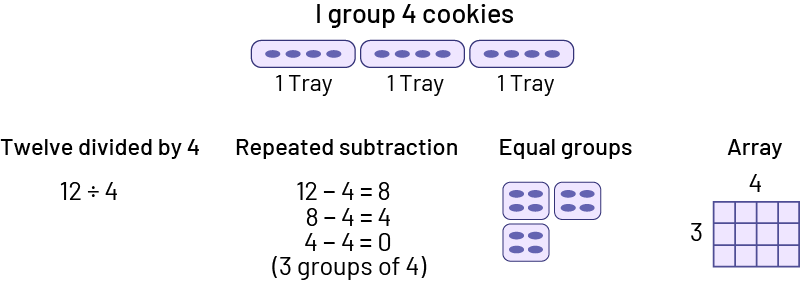
- Twelve cookies were baked. If 3 trays were used with the same number of cookies on each tray, how many cookies were on each tray?
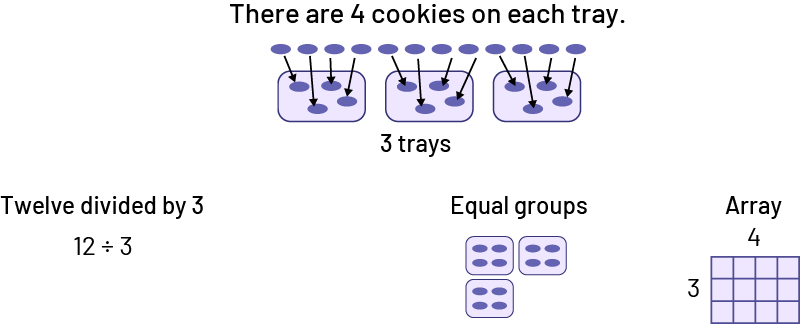
You can also present a variety of everyday items placed in arrays (for example, egg cartons, juice boxes, packages of small yogurt containers, muffin tins) and ask how to determine the number of items. Some count one by one, but many intuitively do repeated addition or even multiplication based on the rows.
Once students understand the model, an array can be used to carry out a computation. This can be done on grid paper.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 134-135.
Example
A skateboard has 4 wheels. How many wheels do 17 skateboards have?
\(17 \times 4 = ?\)
Using the commutative property, I change the multiplication to \(4 \times 17\). It is easier to visualize 4 rows of 17 small squares. I decompose 17 to \(10\; + \;7\).
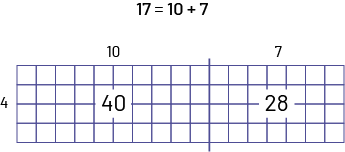
\(40 + 28 = 68\)
There are 68 wheels on 17 skateboards.
Example
At Northern Star School, there are 6 classes of 24 students. How many students are there in all?
\[6 \times 24 = ?\]
Distributive Property Using the Array Model
To better calculate the number of squares, thick lines are drawn to delineate the groupings of 10 in the second factor.
\(\left( {24\; = \;10\; + \;10\; + \;4} \right)\)
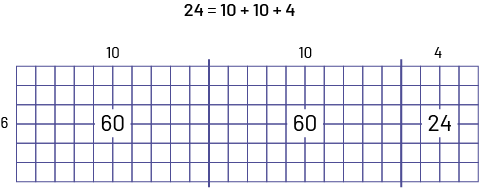
\(\begin{array}{l}60 + 60 + 24 &= 120 + 24 &= 144\end{array}\)
There are 144 students in all.
This representation is similar to an array created with base ten blocks.
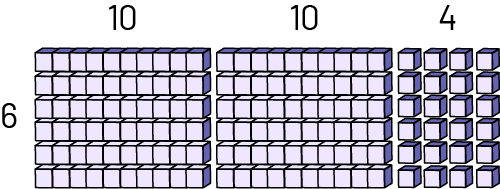
\(\begin{array}{l}60 + 60 + 24 &= 120 + 24 &= 144\end{array}\)
In the previous examples, all rows and columns are delineated. Therefore, each unit is identifiable. Over time, students can represent the same situation differently by creating various arrays where each unit is not represented. For example, the following three more arrays also represent \(6\; \times \;24\), using open arrays.

\(\begin{align}6 \times 24 &= (6 \times 2 \;{\rm{tens)}} + (6 \times 4 \;{\rm{ones}})\\ &= 12 \;{\rm{tens}} + 24 \;{\rm{ones}}\\ &= 12 \;{\rm{tens}} + (2 \;{\rm{tens}} + 4 \;{\rm{ones}})\\ &= 14 \;{\rm{tens}} + 4 \;{\rm{ones}}\\ &= 144\end{align}\)

\(\begin{align}6 \times 24 &= (6 \times 20{\rm{)}} + (6 \times 4)\\ &= 120 + 24\\ &= 144\end{align}\)

\(\begin{align}6 \times 24 &= (6 \times 10{\rm{)}} + (6 \times 10) + (6 \times 4)\\ &= 60 + 60 + 24\\ &= 120 + 24\\ &= 144\end{align}\)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 135-136.
As students develop the ability to use the open arrays and the area model and understand the strategy of adding partial products related to the concept of area, they are able to solve multiplication problems on larger numbers. We can break down each of the two factors into tens and ones. The area model is useful for representing decomposition and partial products as illustrated in the following example:
There are 5 rides at the fair. Each ride accommodates 27 people. How many people can be on all the rides?

When the number 27 is decomposed into 20 and 7, we find ourselves distributing the product \(5 \times \;27\) to the sum of two easily calculated partial products, that is, \(\left( {20 \times \;5} \right)\; + \;\left( {7 \times \;5} \right)\), for a total of 135 people.
At this time, teachers may suggest that students record these partial products in a place-value table as follows:
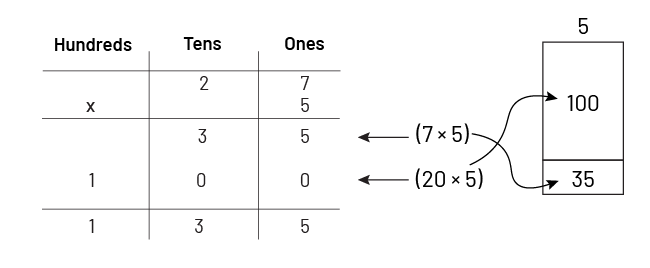
The order in which students record their partial products in the table is not important. Once students have mastered the use of a place value table to record the partial products associated with any multiplication, teachers can introduce the standard multiplication algorithm. It is important to emphasize the connection between the steps in the algorithm and the steps in the place-value table. Students will then understand that the standard algorithm for multiplication is just a quick way to reduce multiplication to a sum of partial products.
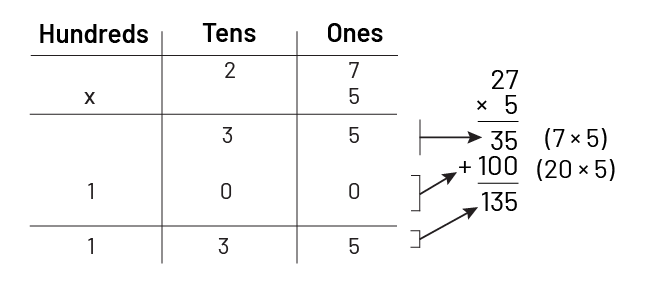
Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 61-64.
Knowledge: The Array
The array can be a model for showing multiplication and division because it structures repeated groups of equal size into rows and columns. The array makes visual connections to skip counting, the distributive property, the inverse relationship between multiplication and division, and the measurement of area. The area model using a rectangle is sometimes referred to as an open array. Even though the area model can be used to represent the multiplication of any two numbers, students may need support to not confuse it with the actual context of the problem.
Open arrays show how a multiplication statement can be thought of as the area of a rectangle \(\left({b\; \times \;h}\right)\). An unknown product is decomposed into partial products (smaller rectangles) with “dimensions” that access known facts and friendly numbers. The partial products are then totalled. Standard algorithms for multiplication are based on the distributive property.
For example: \(5\; \times \;78\)

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8 2020, Ontario Ministry of Education.
Knowledge: Tree Diagram
A branching diagram highlights all the possible combinations or outcomes for two or more independent events so that they can be counted.
Example
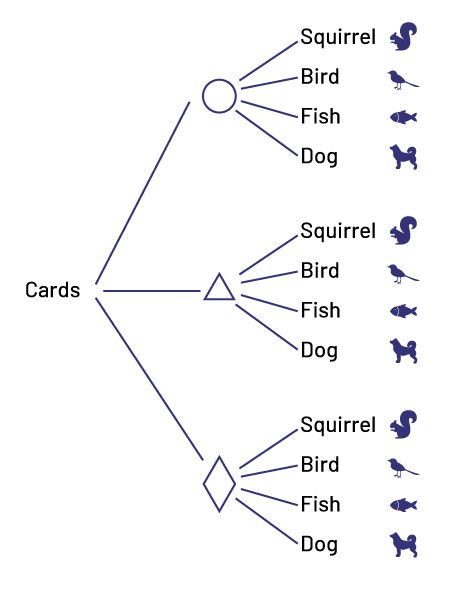
Source: adapted and translated from Les mathématiques...un peu, beaucoup, à la folie!, Guide pédagogique Traitement des données et probabilité, 6e année, module 1, p. 215.
