GEEM - Enseignement et apprentissage

B1.4 Comparer et ordonner des fractions à partir des demis jusqu’aux douzièmes, y compris des fractions impropres et des nombres fractionnaires, dans divers contextes.

Activité 1 : la comparaison de fractions

Écrire au tableau un ensemble de fractions entre 0 et 2 (par exemple, $\frac{5}{6},\;\frac{5}{8},\;\frac{4}{4},\;\frac{5}{3},\;\frac{9}{{10}},\;1\frac{2}{3},\;\frac{8}{5},\;\frac{3}{5}$).

Inviter les élèves à classer ces nombres ainsi : ceux qui sont près de 0, ceux qui sont près de $\frac{1}{2}$, ceux qui sont près de 1 et ceux qui sont près de 2. Ensuite, en s’attardant aux fractions qui sont près de $\frac{1}{2}$, leur demander de désigner celles qui sont supérieures à $\frac{1}{2}$ et celles qui lui sont inférieures.

Dessiner ensuite une droite numérique en situant les nombres $0,\;\frac{1}{2},\;1,\;1\frac{1}{2}\;\rm{et} \ 2$ puis inviter des élèves à venir situer les nombres écrits au tableau sur cette droite numérique en expliquant leur choix.

Une droite numérique de zéro à 2 graduée par intervalles d’un demi.

Refaire l’exercice en utilisant d’autres critères de classement (par exemple, entre 0 et 1, entre 1 et 2) ou en utilisant d’autres nombres.

Source: Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 163.

Activité 2 : quelle clé choisir?

Cette activité permet aux élèves d’examiner l’utilisation de fractions pour définir les mesures d’outils (clés, boulons, écrous).

Matériel

boulons et écrous de dimensions variées préalablement agencées;
ensemble de clés identifiées en mesure impériale (exemples de mesures les plus courantes : $\frac{1}{4}$ pouce, $\frac{3}{8}$ pouce, $\frac{1}{2}$ pouce, $\frac{5}{8}$ pouce, $\frac{3}{4}$ pouce).

Démarche

Le personnel enseignant invite les élèves à s’asseoir en cercle autour du matériel disposé sur le sol. Il explique aux élèves que le système métrique est le système de mesures généralement utilisé au Canada, mais que dans certains domaines comme en construction, le système impérial est encore couramment utilisé.

Le personnel enseignant montre ensuite aux élèves une clé sur laquelle est inscrite une fraction et explique que la mesure de l’ouverture de cette clé correspond à une fraction d’un pouce. Par exemple, la clé sur laquelle la fraction $\frac{3}{4}$ est inscrite a une ouverture de $\frac{3}{4}$ pouce. Au besoin, il montre un pouce sur une règle ou sur un ruban gradué et précise que le pouce est une mesure représentant approximativement 2,5 cm. Ensuite, elle ou il explique que la clé est l’outil utilisé afin de serrer un écrou et qu’il faut s’assurer que la mesure de l’ouverture de la clé correspond à la largeur de l’écrou.

Le personnel enseignant présente aux élèves les fractions correspondant aux clés et aux écrous apportés. Les fractions peuvent être écrites au tableau ou sur une grande feuille de papier.

Ensuite, il choisit un écrou (partiellement vissé sur un boulon), le fait circuler parmi les élèves et leur demande d’estimer sa largeur en pouce afin de déterminer quelle clé doit être utilisée pour le visser ou le serrer.

Le personnel enseignant invite l’élève à essayer de serrer l’écrou en question en utilisant la clé de son choix. Si la clé ne correspond pas avec précision à l’écrou, l’élève doit indiquer si la clé choisie est trop grande ou trop petite. Par exemple, l’élève (photo ci-dessous) explique qu’il a choisi la clé de $\frac{5}{8}$ pouce, mais qu’elle est un peu trop grande.

Si le 1^er essai est infructueux, les élèves tentent de déterminer à nouveau quelle clé devrait être utilisée. Le personnel enseignant invite d’autres élèves à faire un essai, et ce, jusqu’à ce que la clé correspondant à l’écrou soit trouvée, puis reprend la même démarche avec d’autres écrous.

Tout au long de l’activité, le personnel enseignant amène les élèves à comparer des fractions (par exemple, l’ouverture de la clé de $\frac{3}{4}$ pouce est plus grande que celle de la clé de $\frac{3}{8}$ pouce) et à justifier leur choix de clé (par exemple, « Lors du dernier essai, la clé de $\frac{1}{2}$ pouce était trop grande; je vais donc essayer celle de $\frac{3}{8}$ pouce, puisque $\frac{3}{8}$ pouce c’est un peu moins que $\frac{1}{2}$ pouce »).

Pour terminer l’activité, le personnel enseignant demande aux élèves de placer les fractions en ordre croissant (par exemple, $\frac{1}{4}$, $\frac{3}{8}$, $\frac{1}{2}$, $\frac{5}{8}$, $\frac{3}{4}$) et de vérifier leur réponse en plaçant les clés correspondantes en ordre de grandeur.

Note : Afin de rendre la tâche plus authentique, au lieu d’écrous et de boulons en vrac, on peut présenter une bicyclette (ou tout autre objet qui comprend plusieurs écrous) et demander, par exemple, aux élèves d’identifier la clé à utiliser pour desserrer l’écrou pour monter le siège ou pour enlever la roue.

Source: Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 105-106.

Activité 3 : en ordre

Matériel

annexe 5.4 (Fractions)

Grouper les élèves par 4. Remettre à chaque équipe une copie de l’annexe 5.4 et faire remarquer que la partie ombrée représente une fraction de la bande. Leur demander de découper entre les bandes de façon à obtenir un ensemble de bandes, chacune accompagnée de la fraction correspondante.

Note : Inviter les élèves à combiner des bandes afin de créer des nombres fractionnaires ou des fractions impropres. L’élève peut aussi se permettre de créer ses propres bandes.

Exemple

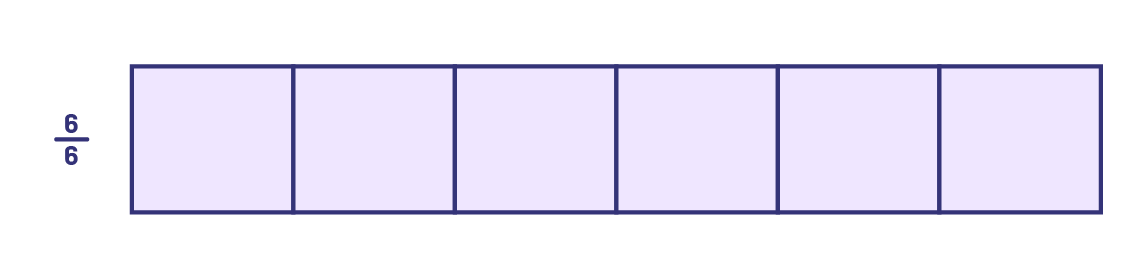
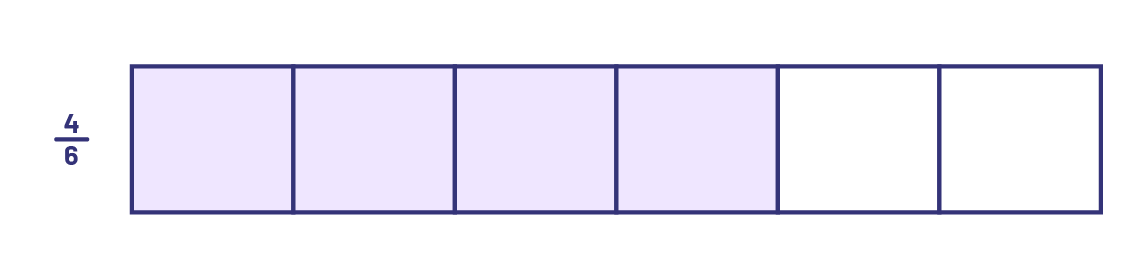
$Une bande qui représente la fraction 6 sur 6. La bande est divisée en 6 parties égales. Elles sont toutes ombragées.$ $Une bande qui représente la fraction 4 sur 6. La bande est divisée en 6 parties égales, 4 parties sont ombragées.$

L’élève crée le nombre fractionnaire $1\frac{4}{6}$ ou la fraction impropre $\frac{{10}}{6}$.

Spécifier ensuite que leur tâche consiste à placer les fractions en ordre croissant (de la plus petite partie à la plus grande).

Circuler et questionner les élèves afin de vérifier leur compréhension. Poser des questions telles que :

Pourquoi avez-vous placé cette fraction à cet endroit?
Comment les nombres au numérateur et au dénominateur vous aident-ils à placer les fractions en ordre?
Certaines fractions représentent la même quantité. Qu’est-ce que cela signifie? Comment avez-vous su où les placer? Comment pouvez-vous justifier qu’elles soient équivalentes?

Lorsque la tâche est terminée, faire un échange mathématique en mettant l’accent sur les stratégies utilisées afin de déterminer l’ordre des fractions. Ensuite, inviter les élèves à observer des fractions unitaires (par exemple, $\frac{1}{2},\;\frac{1}{3},\;\frac{1}{4},\;\frac{1}{6},\;\frac{1}{8},\;\frac{1}{9},\;\frac{1}{{12}}$), plus particulièrement leur numérateur et leur dénominateur afin de faire ressortir que lorsque des fractions ont le même numérateur, celle qui a le plus grand dénominateur représente une part plus petite. Puis, les inviter à comparer toutes les fractions ayant un même dénominateur (par exemple, $\frac{1}{8},\;\frac{2}{8},\;\frac{3}{8} \ldots $) afin de faire ressortir que lorsque des fractions ont le même dénominateur, celle qui a le plus grand numérateur représente une part plus grande. Finalement, les inviter à analyser des fractions équivalentes afin de reconnaître la relation de proportionnalité.

Source: Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 160.