B1.5 Lire, représenter, comparer et ordonner des nombres décimaux jusqu’aux centièmes, dans divers contextes.
Activité 1 : la mesure en décimale
Cette activité intègre des concepts en Nombres et en Sens de l’espace.
Tout au long de leur parcours scolaire, les élèves utilisent différentes unités de mesure conventionnelles pour estimer, déterminer et enregistrer des mesures. Or, au cycle moyen, ces mesures deviennent de plus en plus précises et sont exprimées à l’aide de nombres décimaux. Puisque le système métrique est un système à base 10, les élèves doivent bien comprendre les concepts de nombre décimal et de valeur de position, ainsi que les relations entre les unités de mesure (par exemple, 1 mm est 10 fois plus petit que 1 cm, 1 m est 100 fois plus grand que 1 cm) pour être capables de s’en servir adéquatement.
La conversion d’une mesure en une autre est souvent ardue pour certaines et certains élèves, particulièrement lorsque le résultat de la conversion est un nombre décimal. De plus, les élèves ont beaucoup de mal à exprimer une mesure en utilisant une seule unité de mesure. Par exemple, elles et ils ont tendance à dire « 1 mètre et 15 centimètres » plutôt que « 1 et 15 centièmes de mètre » et à écrire « 1 m 15 cm » plutôt que « 1,15 m ».
La présente activité vise à amener les élèves à exprimer une mesure à l’aide d’une seule unité de mesure. Elle mise sur la compréhension des relations entre les unités de mesure et sur la valeur de position plutôt que sur l’utilisation de procédures (par exemple, déplacer la virgule vers la gauche ou vers la droite selon les unités retenues).
Montrer une corde aux élèves et indiquer sa longueur en utilisant 2 unités de mesure distinctes (par exemple, 4 dm et 5 cm). Ensuite, tracer au tableau des segments représentant ces unités de mesure.
Voici 2 exemples de représentations.
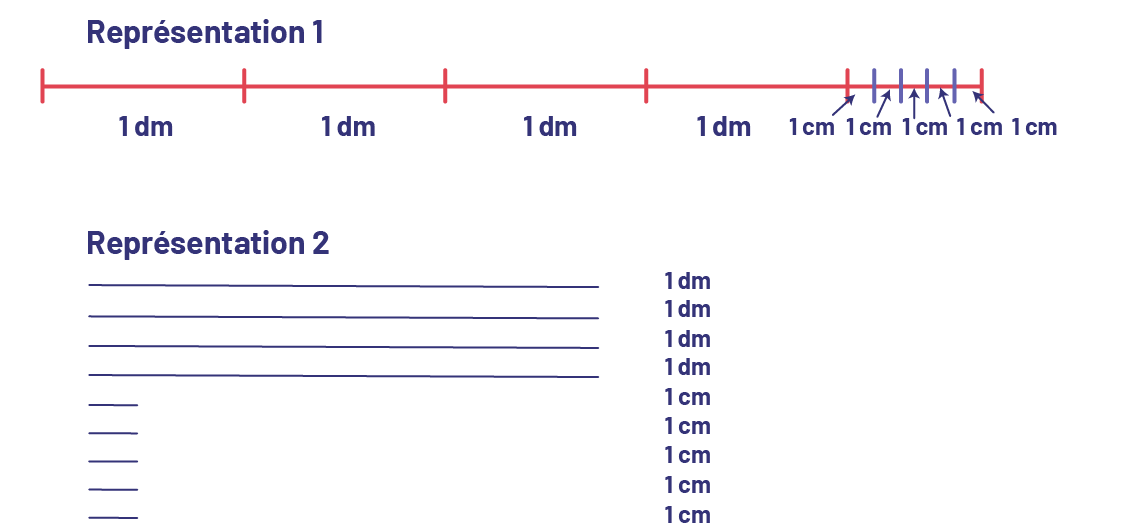
Inviter alors les élèves à exprimer la longueur de la corde de différentes façons à l’aide d’une seule unité de mesure.
Note : Des mètres séparés en décimètres et en centimètres, des décimètres séparés en centimètres et en millimètres sont des représentations visuelles utiles pour acquérir une compréhension conceptuelle des unités de mesure.
Inviter ensuite les élèves à partager leur réponse et à la justifier en utilisant la représentation au tableau.
Voici 2 exemples de ce qu’elles et ils pourraient écrire.
image Représentation un.Un segment gradué en décimètres, 4 fois, puis gradué en centimètres, 5 fois. Le segment mesure 4 virgule 5 décimètres.Le segment est ensuite gradué en centimètres, un décimètre égal dix centimètres, donc le segment mesure 45 centimètres.Le segment est ensuite gradué en mètre, un décimètre égal zéro virgule un mètre, donc le segment mesure zéro virgule 45 mètre.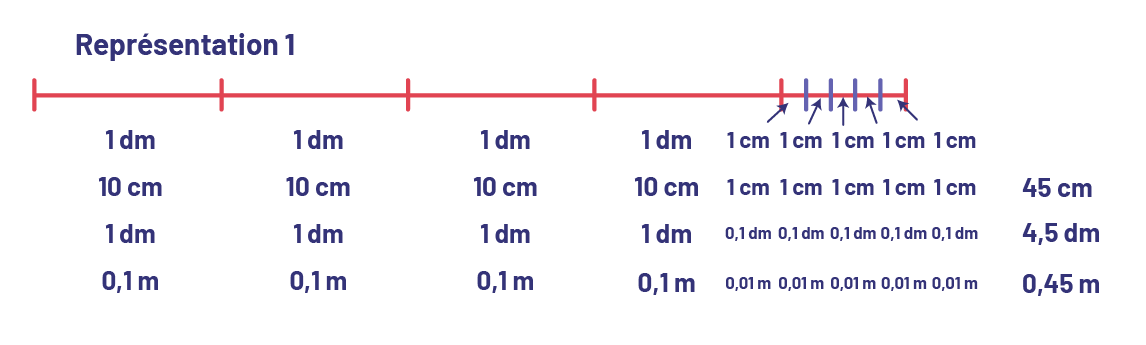
 image Représentation 2.Quatre traits sont tracés, ils mesurent un décimètre. 5 traits plus petits sont en dessous, ils mesurent un centimètre. En additionnant, les traits mesurent 4 virgule 5 décimètres. Ensuite, diverses unités de mesure sont utilisées pour les traits, les centimètres, les décimètres et les mètres.Les grands traits mesurent dix centimètres et les petits traits un centimètre. En additionnant, on obtient 45 centimètres.Les grands traits mesurent zéro virgule un mètre, et les petits traits zéro virgule zéro un mètre. En additionnant, on obtient zéro virgule 45 mètre.
image Représentation 2.Quatre traits sont tracés, ils mesurent un décimètre. 5 traits plus petits sont en dessous, ils mesurent un centimètre. En additionnant, les traits mesurent 4 virgule 5 décimètres. Ensuite, diverses unités de mesure sont utilisées pour les traits, les centimètres, les décimètres et les mètres.Les grands traits mesurent dix centimètres et les petits traits un centimètre. En additionnant, on obtient 45 centimètres.Les grands traits mesurent zéro virgule un mètre, et les petits traits zéro virgule zéro un mètre. En additionnant, on obtient zéro virgule 45 mètre.
Par la suite, présenter d’autres situations similaires et poursuivre avec des situations comportant plusieurs unités de mesure distinctes, par exemple, une corde dont la longueur est de 3 mètres, 2 décimètres et 5 centimètres (3,25 m).
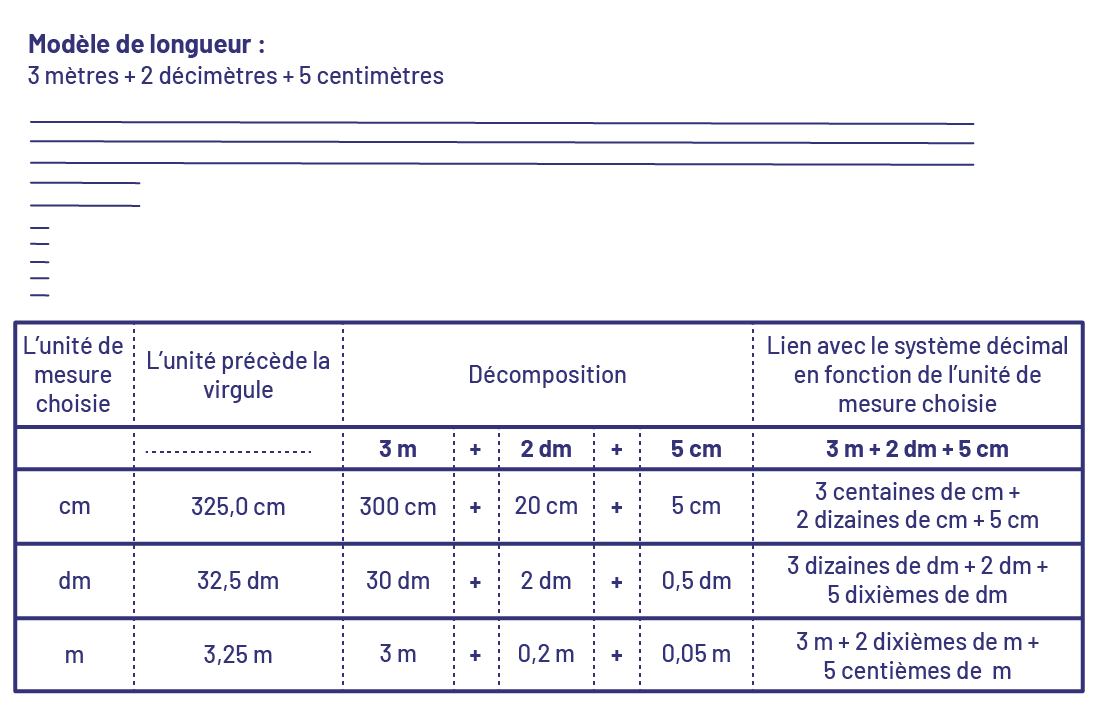 image Modèle de longueur :3 mètres plus 2 décimètres plus 5 centimètres.Les mesures sont représentées individuellement, par un trait qui illustre la corde.Dans un tableau, les renseignements suivants sont consignés :Colonne un :L’unité de mesure choisie : le centimètre, le décimètre et le mètre.Colonne 2 :L’unité précède la virgule . 325 centimètres. 35 virgule 5 décimètres. 3 virgule 25 mètres.Colonne 3 :Décomposition.3 mètres plus 2 décimètres plus 5 centimètres, ou,300 centimètres plus 20 centimètres plus 5 centimètres, ou 30 décimètres plus 2 décimètres plus zéro virgule 5 décimètre, ou,3 mètres plus zéro virgule 2 décimètre plus zéro virgule zéro 5 mètre.Colonne 4 :Lien avec le système décimal en fonction de l’unité de mesure choisie.3 mètres plus 2 décimètres plus 5 centimètres.
image Modèle de longueur :3 mètres plus 2 décimètres plus 5 centimètres.Les mesures sont représentées individuellement, par un trait qui illustre la corde.Dans un tableau, les renseignements suivants sont consignés :Colonne un :L’unité de mesure choisie : le centimètre, le décimètre et le mètre.Colonne 2 :L’unité précède la virgule . 325 centimètres. 35 virgule 5 décimètres. 3 virgule 25 mètres.Colonne 3 :Décomposition.3 mètres plus 2 décimètres plus 5 centimètres, ou,300 centimètres plus 20 centimètres plus 5 centimètres, ou 30 décimètres plus 2 décimètres plus zéro virgule 5 décimètre, ou,3 mètres plus zéro virgule 2 décimètre plus zéro virgule zéro 5 mètre.Colonne 4 :Lien avec le système décimal en fonction de l’unité de mesure choisie.3 mètres plus 2 décimètres plus 5 centimètres.
Note : Il importe également que les élèves comprennent que la conversion n’affecte en rien la longueur de l’objet en question; il s’agit de différentes représentations d’une même longueur.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 117-119.
Activité 2 : la course
La mise en situation suivante est partagée avec les élèves :
Un groupe d’élèves termine une course de bicyclette. Voici les distances parcourues :
- Élève 1 : 4,55 km
- Élève 2 : 4,5 km
- Élève 3 : 5,01 km
- Élève 4 : 5,10 km
- Élève 5 : 4,9 km
Demander aux élèves de représenter et d’ordonner les distances parcourues à l’aide de symboles, d’illustrations, du matériel de base 10 ou de mots. Les élèves comparent, par la suite, leur représentation avec ceux des autres. Animer un échange mathématique pour permettre aux élèves de discuter des diverses méthodes de représentation.
