B1.5 Read, represent, compare, and order decimal numbers up to hundredths, in various contexts.
Activity 1: Measuring With Decimal Numbers
This activity integrates concepts from the Number and Spatial Sense strands.
Throughout their school careers, students use a variety of conventional units of measurement to estimate, determine and record measurements. In the junior grades, these measurements become increasingly precise and are expressed using decimal numbers. Since the metric system is a base ten system, students need to understand the concepts of decimal number and place value, as well as the relationships between units of measurement (for example, 1 mm is one tenth as large as 1 cm, 1 m is 100 times larger than 1 cm) in order to use them appropriately and move flexibly between them.
Converting from one measure to another is often difficult for some students, especially when the result of the conversion is a decimal number. In addition, students may find it very difficult to express a measurement using a single unit of measurement. For example, they tend to say "1 metre and 15 centimetres" rather than "1 and 15 hundredths of a metre" and to write "1 m 15 cm" rather than "1.15 m".
The aim of this activity is to have students express a measurement using a single unit of measure. It focuses on understanding the relationships between units of measurement and on place value, rather than on the use of procedures, such as move the decimal point to the left or to the right.
To begin, show students a string and indicate its length using two different units of measurement (for example, 4 dm and 5 cm). Then draw segments on the board representing these units of measurement. Metres separated into decimetres and centimetres, and decimetres separated into centimetres and millimetres are useful visual representations for gaining a conceptual understanding of units of measure.
Below are two examples of representations:
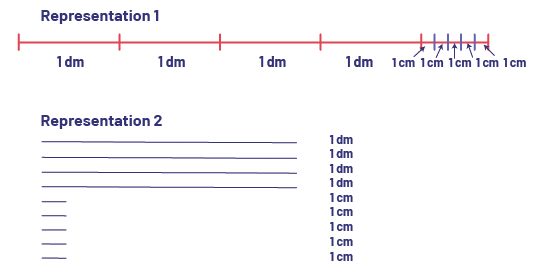
Then invite students to express the length of the rope in different ways using a single unit of measurement.
Next invite students to share their answer and justify it using the representation on the board.
Possible representations include:


Then introduce other similar situations. Continue with situations that involve several different units of measurement, for example, a rope that is 3 metres, 2 decimetres and 5 centimetres long (3.25 m).
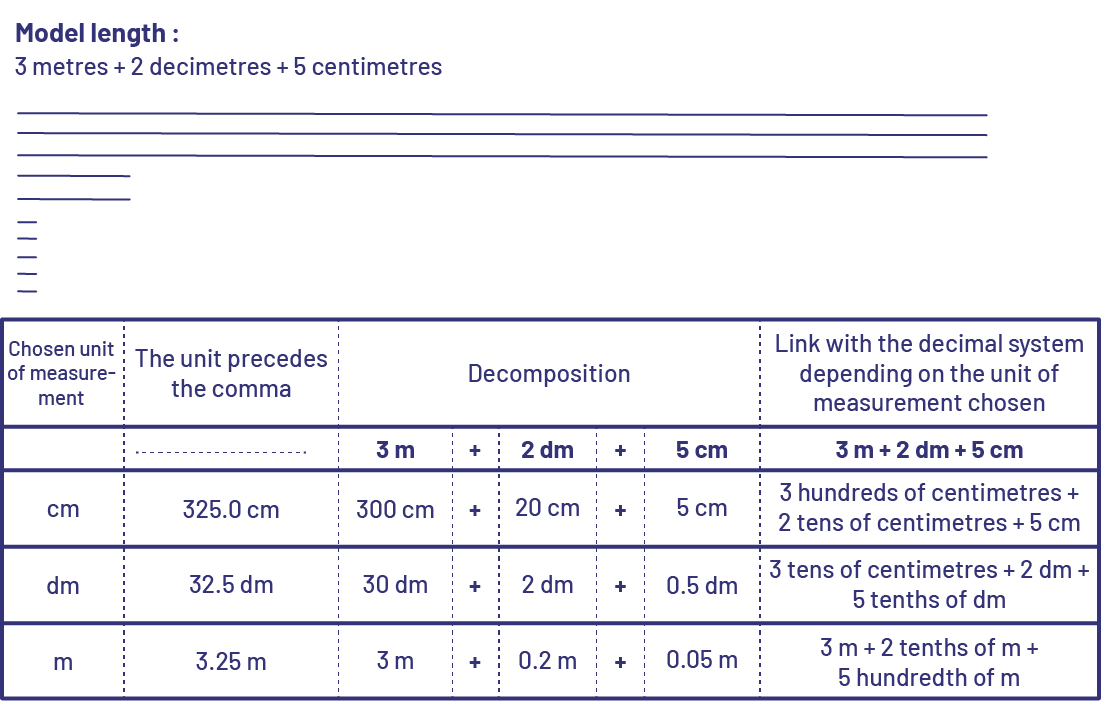
Note: It is also important for students to understand that the conversion does not affect the length of the object in question; they are different representations of the same length.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 117-119.
Activity 2: The Race
The following situation is shared with students:
A group of students participated in a bicycle race and completed the following distances:
- Student 1: 4.55 km
- Student 2: 4.5 km
- Student 3: 5.01 km
- Student 4: 5.10 km
- Student 5: 4.9 km
Ask students to represent and order the distances travelled using symbols, pictures, base ten blocks, or words. Students then compare their representations with those of others. Facilitate a math conversation to allow students to talk about the various methods of representation.
