B2.1 Utiliser les propriétés des opérations et les relations entre les opérations pour résoudre des problèmes comprenant des nombres naturels et des nombres décimaux, y compris des problèmes nécessitant plus d’une opération, et vérifier la vraisemblance des calculs.
Activité 1 : trios
Stratégie : la commutativité (addition ou multiplication)
Matériel
- un jeu de cartes Trios pour les additions ( annexe FR15 et annexe FR16) ou préparer des cartes d’additions selon le niveau d’études
- un jeu de cartes Trios pour les multiplications ( annexe FR17 et annexe FR18) ou préparer des cartes de multiplications selon le niveau d’études
Cette activité se fait avec toute la classe. Chaque élève reçoit 1 carte du jeu des Trios. Une fois les cartes distribuées, les élèves cherchent les autres membres de leur trio. Il leur faut connaître la réponse à la question, ou envisager les questions possibles si leur carte porte une réponse. Par exemple, les trios pourraient être \(3\; + \;5,\;5\; + \;3\;{\rm{et}}\;{\rm{8}}\); ou \(3\; \times \;6,\;6\; \times \;3\;{\rm{et}}\;18\). Lorsqu’un trio est complet, les 3 élèves s’assoient ensemble. Une fois que tous les élèves sont assis, chaque trio présente les cartes de commutativité à la classe.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 78.
Activité 2 : vraie ou fausse?
Afin d’explorer les propriétés des opérations, animer une mini-leçon en regroupant les élèves et en écrivant ces phrases mathématiques une à la fois. Pour chacune, demander aux élèves de déterminer si la phrase est vraie ou fausse.
Par exemple, pour la propriété de la distributivité, écrire ces phrases une à la fois.
\(47\; \times \;21\; = \;\left( {40\; \times \;20} \right)\; + \;\left( {40\; \times \;1} \right)\; + \;\left( {7\; \times \;20} \right)\; + \;\left( {7\; \times \;1} \right)\)
\(92\; \times \;34\; = \;\left( {90\; \times \;30} \right)\; + \;\left( {90\; \times \;4} \right)\; + \;\left( {2\; \times \;30} \right)\; + \;\left( {2\; \times \;4} \right)\)
\(\left( {40\; \times \;50} \right)\; + \;\left( {40\; \times \;0} \right)\; = \;2\;000\)
Il est important aussi de montrer le raisonnement des élèves avec des traces, soit en rayant des nombres de chaque côté ou de mettre des arcs entre les nombres. Il est bien aussi de montrer le raisonnement en utilisant une droite numérique ouverte double.
Activité 3 : que vois-tu?
Montrer une image aux élèves d’objets (par exemple, des fruits) placés sous forme de disposition rectangulaire.
Exemple
 image 9 ensembles de fraises en tout.6 ensembles de 20 fraises chacun disposé en 2 colonnes de 3 ensembles.Les ensembles de 20 sont constitués de 5 fraises de large par 5 fraises de haut.3 ensembles de dix fraises chacun disposés en une rangée.Les ensembles de dix fraises sont constitués de 2 fraises de large par 5 fraises de haut.
image 9 ensembles de fraises en tout.6 ensembles de 20 fraises chacun disposé en 2 colonnes de 3 ensembles.Les ensembles de 20 sont constitués de 5 fraises de large par 5 fraises de haut.3 ensembles de dix fraises chacun disposés en une rangée.Les ensembles de dix fraises sont constitués de 2 fraises de large par 5 fraises de haut.
En dyades, demander aux élèves d’observer l’image et de trouver autant d’opérations qui peuvent la représenter.
Par exemple : \(15\; \times \;12\; = \;180\)
Jumeler les dyades pour que les élèves puissent comparer leurs opérations.
Faire une mise en commun afin de faire ressortir des propriétés et des relations.
Exemples
Commutativité
\(12\; \times \;15\; = \;180\)
\(15\; \times \;12\; = \;180\)
Distributivité
\(12\; \times \;15\; = \;\left( {10\; \times \;15} \right)\; + \;\left( {2\; \times \;15} \right)\)
\(12\; \times \;15\; = \;\left( {10\; \times \;10} \right)\; + \;\left( {10\; \times \;5} \right)\; + \;\left( {2\; \times \;10} \right)\; + \;\left( {2\; \times \;5} \right)\)
Relation d’opération inverse de la multiplication et de la division
\(12\; \times \;15\; = \;180\)
\(180\; \div \;15\; = \;12\)
\(15\; \times \;12\; = \;180\)
\(180\; \div \;12\; = \;15\)
Activité 4 : un beau zéro
Stratégie : règles relatives à 0 et à 1 (dans la multiplication)
Matériel
- annexe FR20 [une roulette Un beau zéro (+ 0, – 0, + 1, × 0, × 1)]
- annexe FR20 (une roulette de nombres selon le niveau d’études)
- annexe FR21 (des feuilles de jeu vierge Un beau zéro) (1 par élève)
- des jetons
Les élèves reçoivent une feuille de jeu vierge et inscrivent dans les cases les nombres de 0 à 8, en les répétant à leur gré jusqu’à ce que toutes les cases soient remplies. Elles et ils travaillent ensuite en groupe de 2, 3 ou 4. L’élève qui ouvre le jeu fait tourner les 2 roulettes et effectue l’opération indiquée. Si la case indiquant la réponse est libre sur sa feuille de jeu, l’élève place un jeton sur le nombre. C’est alors au tour de l’élève qui suit de jouer. Lorsqu’il y a déjà un jeton sur le nombre voulu, c’est au tour de l’élève qui suit de jouer. Le jeu continue jusqu’à ce qu’un ou une élève ait réussi à remplir toutes les cases d’une rangée sur sa feuille de jeu.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 80.
Activité 5 : des opérations apparentées
Écrire au tableau ou sur du papier-charte, chacune des séries d’opérations apparentées suivantes, une à la fois, et demander aux élèves d’effectuer les opérations qu’elle contient.
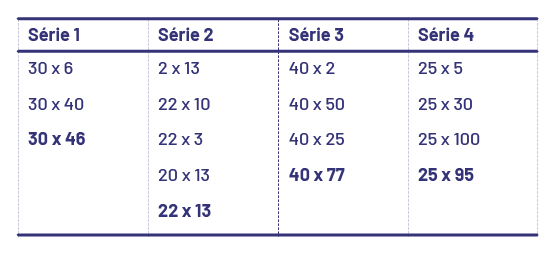 image Tableau montrant 4 séries d’opérations inscrites en colonne. Dans chaque série, la dernière opération est en gras.Série un:-30 fois 6-30 fois 40-30 x 46Série 2:-2 fois 13-22 fois dix-22 fois 3-20 fois 13-22 fois 13Série 3:-40 fois 2-40 fois 50-40 fois 25-40 fois 77Série 4:-25 fois 5-25 fois 30-25 fois 100-25 fois 95
image Tableau montrant 4 séries d’opérations inscrites en colonne. Dans chaque série, la dernière opération est en gras.Série un:-30 fois 6-30 fois 40-30 x 46Série 2:-2 fois 13-22 fois dix-22 fois 3-20 fois 13-22 fois 13Série 3:-40 fois 2-40 fois 50-40 fois 25-40 fois 77Série 4:-25 fois 5-25 fois 30-25 fois 100-25 fois 95
Une fois une série complétée, faire ressortir les diverses stratégies de calcul mental en posant des questions telles que :
- Comment avez-vous résolu la dernière opération?
- Pour résoudre la dernière opération, avez-vous utilisé certains éléments des opérations précédentes?
- Avez-vous résolu les opérations dans l’ordre?
Si nécessaire, avant d’effectuer la même démarche avec la série suivante, présenter d’autres exemples d’opérations apparentées similaires.
Si les élèves ont de la difficulté à voir et à mettre en application la distributivité de la multiplication pour résoudre la dernière opération de chaque série, les y amener en représentant ces opérations sous forme de dispositions rectangulaires.
Exemple
Constatations sur chacune des séries
Série 1
Cette série permet de revoir la propriété de distributivité de la multiplication sur l’addition à sa plus simple expression. Il s’agit de reconnaître que pour obtenir le produit de \(30 \times 46\), il est possible d’effectuer une opération sur une somme de termes et d’obtenir le même résultat que si l’opération avait été effectuée sur chaque terme, c’est-à-dire :
\(30\; \times \;46\; = \;30\; \times \;\left( {40\; + \;6} \right)\)
\(30\; \times \;46\; = \;\left( {30\; \times \;40} \right) + \;\left( {30\; \times \;6} \right)\)
Série 2
Cette série permet de constater que la décomposition reliée à la distributivité peut s’effectuer aussi bien sur le 2e terme que sur le 1er, soit :
\(\begin{array}{l}22\; \times \;13\; = \;\left( {20\; \times \;13} \right) + \;\left( {2\; \times \;13} \right)\;{\rm{ou}}\\22\; \times \;13\; = \;\left( {22\; \times \;10} \right) + \;\left( {22\; \times \;3} \right)\end{array}\)
Série 3
Cette série permet de constater que la décomposition d’un nombre pour appliquer la distributivité peut se faire en plus de 2 parties. Par exemple :
\(40\; \times \;77\; = \;40\; \times \;\left( {50\; + \;25\; + \;2} \right)\)
\(40\; \times \;77\; = \;\left( {40\; \times \;50} \right)\; + \;\left( {40\; \times \;25} \right)\; + \;\left( {40\; \times \;2} \right)\)
Série 4
Cette série permet de constater que l’on peut résoudre la dernière opération à l’aide de la distributivité de la multiplication sur la soustraction. Par exemple :
\(25\; \times \;95\; = \;25\; \times \;\left( {100\; - \;5} \right)\)
\(25\; \times \;95\; = \;\left( {25\; \times \;100} \right) - \;\left( {25\; \times \;5} \right)\)
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 221-222.
