B2.4 Représenter et résoudre des problèmes relatifs à l’addition de nombres naturels dont la somme est égale ou inférieure à 100 000 et à la soustraction de nombres naturels égaux ou inférieurs à 100 000, et l’addition et la soustraction de nombres décimaux jusqu’aux centièmes, à l’aide d’outils et de stratégies appropriés, et d’algorithmes.
Activité 1 : addition de nombres décimaux
Présenter les différentes situations aux élèves :
Une planche à roulettes coûte 35,98 $. Le casque, les protège-coudes, les protège-genoux et les protège-poignets coûtent respectivement 19,99 $, 7,90 $, 12,89 $ et 9,99 $. Combien Lucie doit-elle payer pour acheter un équipement complet à sa fille?
Stratégie de compensation
Il manque 0,25 $ pour avoir des montants complets (sans partie décimale).
Donc, \(36\;\$ \; + \;20\;\$ \; + \;8\;\$ \; + \;13\;\$ + \;10\;\$ \; = \;87\;\$ \;\;\;{\rm{et}}\;\;\;87\;\$ \; - \;0,25\;\$ \; = \;86,75\;\$ \;\)
Donc, Lucie devra payer 86,75 $ pour acheter l’équipement de sa fille.
Une station de météorologie a noté les précipitations du mois de mai. Voici les quantités en millimètres pour les 5 journées de pluie du mois : 1,2 mm, 0,8 mm, 2,1 mm, 8,9 mm et 4,7 mm. Quelle est la quantité totale de précipitations pour le mois de mai?
Stratégie de calcul mental
1,2 et 0,8 donnent 2
2,1 et 8,9 donnent 11
2 et 11 donnent 13
13 et 4,7 donnent 17,7
Donc, il est tombé 17,7 mm de pluie en mai.
Un terrain rectangulaire a les dimensions suivantes : 40,5 m sur 80,25 m. Quelle est la longueur de la clôture qui entoure complètement ce terrain?
Algorithme personnel
image
Une addition verticale est placée dans un tableau en respectant une valeur de position par case, plus une case pour la
virgule.40, virgule 5 plus 80, virgule 85, égal. 4 et 8, des dizaines, sont additionnés, on obtient 12. 5 et 8, des
dixièmes, sont additionnés, on obtient, 13.Le 5 des centièmes est simplement reporté sous la barre des égales.On
obtient le résultat 121 virgule 35.
\(121,35 + 121,35 = 242,7\)
La longueur de la clôture qui entoure complètement le terrain est de 242,7 m.
Une aire de jeux carrée a des côtés de 12,5 m.
- Quel est le périmètre de cette aire de jeux?
- Quel est le périmètre d’une aire de jeux dont les côtés sont 3 fois plus longs?
Algorithme personnel
-
\(\begin{align}\;12,5\; + \;12,5\; &= \;25 \\ \;25\ + \;25\; &= \;50 \end{align}\)
Donc, le périmètre de l’aire de jeux est de 50 m.
-
\(\begin{align}\;12,5\; + \;12,5\; + \;12,5 &= 25\; + \;12,5 \\ &= \;37,5 \end{align}\)
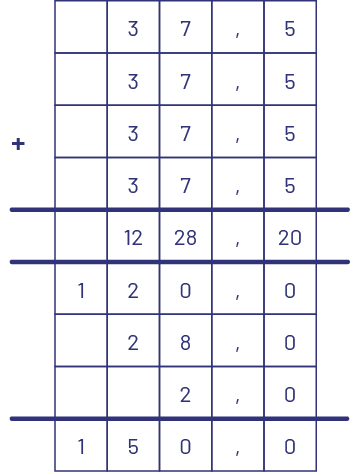image Une addition verticale est placée dans un tableau en respectant une valeur de position par
case, plus une case pour la virgule.37, virgule 5 plus 37, virgule 5 plus 37, virgule 5, plus 37 virgule 5, égal.Les 5
sont additionnés, on obtient 20.Les 7 sont additionnés, on obtient, 28.Les 3 sont additionnés, on obtient 12.Les
résultats de ces additions sont placés dans le tableau ont obtient l’addition suivante. 120 plus 28 plus 2 égal
150.
Donc, le périmètre de l’aire de jeux est de 150 m.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activité 2 : capitaine, veux-tu?
Présenter la situation suivante aux élèves :
Aujourd’hui, vous allez participer à une course un peu spéciale. Chaque participante ou participant doit parcourir un trajet de 10 mètres en effectuant au moins une fois chacune des foulées présentées dans le tableau ci-dessous.
Foulée : Pas de géant
Longueur : 1,3 m
Foulée : Pas de souris
Longueur : 0,27 m
Foulée : Saut de grenouille
Longueur : 0,5 m
Foulée : Bond de kangourou
Longueur : 2,36 m
Avant de commencer, vous devez planifier les étapes de votre trajet. Chaque étape représente un déplacement équivalant à une ou plusieurs fois une même foulée. Au terme de toutes les étapes, vous ne devez pas dépasser la ligne d’arrivée de plus de 1 mètre. Vous devez calculer la distance parcourue à chaque étape ainsi que la distance totale parcourue après chacune des étapes.
Exemple| Étape 1 | Étape 2 | Étape 3 | Étape 4 | |
|---|---|---|---|---|
| Foulées | 8 sauts de grenouille | 1 bond de kangourou | 2 pas de géant | 6 pas de souris |
| Distance parcourue à chaque étape | 4 m | 2,36 m | 2,6 m | 1,62 m |
| Distance totale parcourue après chaque étape | 4 m | 6,36 m | 8,96 m | 10,58 m |
Allouer suffisamment de temps pour que les élèves puissent planifier leur trajet. Grouper les élèves par 3, nommer une ou un capitaine par équipe, puis expliquer le fonctionnement du jeu :
La ou le capitaine est le maître du jeu. Les 2 autres élèves lui demandent, à tour de rôle, la permission d’entreprendre une étape de son trajet, en disant par exemple : « Capitaine, veux-tu que je fasse 8 sauts de grenouille pour avancer de 4 mètres? » À ce moment, la ou le capitaine roule un dé et donne sa réponse en fonction du nombre obtenu sur le dé : si le nombre est 1, 2, 3 ou 4, elle ou il accepte; sinon, elle ou il refuse.
Si la demande est acceptée, la participante ou le participant franchit la distance prévue et indique la distance totale parcourue depuis la ligne de départ. En cas de refus, elle ou il ne bouge pas et doit attendre au prochain tour pour refaire la même demande.
La ou le capitaine a également la responsabilité de vérifier, au besoin à l’aide de la calculatrice, les calculs effectués par la participante ou le participant. S’il y a erreur, la ou le capitaine ordonne à la participante ou au participant de retourner à la case départ.
La 1re personne à franchir la ligne d’arrivée (10 mètres) gagne.
Le trajet peut être effectué en déplaçant un pion sur un ruban, en indiquant les distances sur une droite numérique ou en effectuant réellement le trajet. Allouer suffisamment de temps pour permettre aux élèves de jouer les 2 rôles (capitaine et participante ou participant).
Exemple
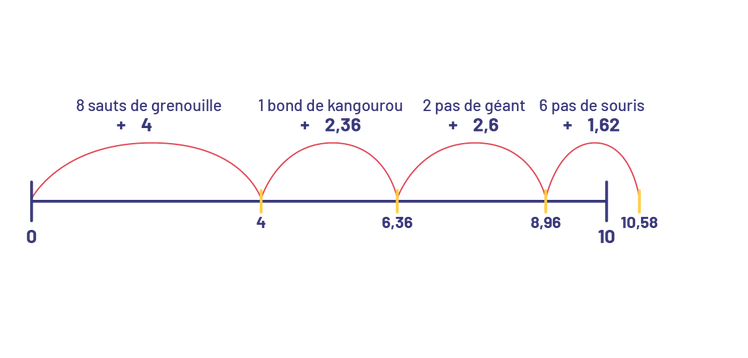image Une
droite numérique de zéro à dix.Un bond de 8 sauts de grenouille, qui part de zéro et va à 4, bond de plus 4.Un bond de
kangourou de plus 2 virgule 36, part de 4 et va à 6 virgule 36.Un bond de 2 pas de géants, plus 2 virgule 6, part de 6
virgule 36 et va à 8 virgule 96.Un bond de 6 pas de souris, plus un virgule 62, qui part de 8 virgule 96 et va à dix
virgule 58.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 157-159.