B2.4 Represent and solve problems involving the addition and subtraction of whole numbers that add up to no more than 100 000, and of decimal numbers up to hundredths, using appropriate tools, strategies, and algorithms.
Activity 1: Addition of Decimal Numbers
Present the different situations to the students:
A skateboard costs $35.98. The helmet, elbow pads, knee pads and wrist pads cost $19.99, $7.90, $12.89 and $9.99 respectively. How much does Lucy have to pay to buy her daughter a complete set of equipment?
Compensation strategy
There is a $0.25 shortfall to have the total amount required when the total is calculated by rounding up to the nearest whole number.
So\(\$36\; +\; \$20 \;+\; \$8 \;+\; \$13 \;+\; \$10 \;+\; \$87\ \text{ and\ } \;\$87 \;-\; \$0.25 \;=\; \$86.75\)
Therefore, Lucie will have to pay $86.75 to buy her daughter's equipment.
A weather station recorded the rainfall for the month of May. It rained on 5 days with the following amounts: 1.2 mm, 0.8 mm, 2.1 mm, 8.9 mm and 4.7 mm. What is the total amount of rainfall for the month of May?
Mental math strategy
1.2 and 0.8 makes 2
2.1 and 8.9 makes 11
2 and 11 makes 13
13 and 4.7 makes 17.7
This means that 17.7 mm of rain fell in May.
A rectangular lot has the following dimensions: 40.5 m by 80.85 m. What is the length of the fence that completely surrounds this lot?
Personal algorithm

A square playground has sides of 12.5 m.
- What is the perimeter of this playground?
- What is the perimeter of a playground whose sides are 3 times longer?
Personal algorithm
-
\(\begin{align}\;12.5\; + \;12.5\; &= \;25 \\ \;25\ + \;25\; &= \;50 \end{align}\)
Therefore, the perimeter of the playground is 50 m.
-
\(\begin{align}\;12.5\; + \;12.5\; + \;12.5 &= 25\; + \;12.5 \\ &= \;37.5 \end {align}\)
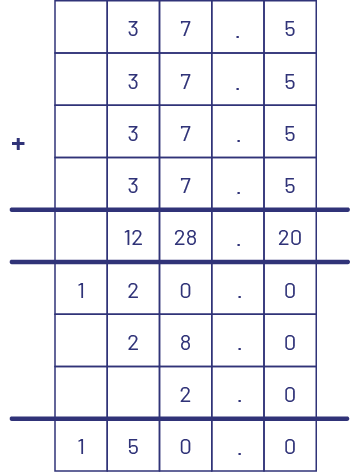
Therefore, the perimeter of the playground is 150 m.
source: translated from L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2: Captain, Will You?
Present the following situation to students:
Today, you'll be taking part in a very special race. Each participant must cover a 10-metre distance, taking at least one of the strides shown in the table below.
Stride: Giant Step
Length: 1.3 m
Stride: Mouse Step
Length: 0.27 m
Stride: Frog Jump
Length: 0.5 m
Stride: Kangaroo Bound
Length: 2.36 m
Before you start, you need to plan the stages of your journey. Each stage represents a movement equivalent to one or more of the same stride. At the end of all the stages, you must not cross the finish line by more than 1 metre. You must calculate the distance covered in each stage and the total distance covered after each stage.
Example| Stage 1 | Stage 2 | Stage 3 | Stage 4 | |
|---|---|---|---|---|
| Strides | 8 frog jumps | 1 kangaroo bounds | 2 giant steps | 6 mouse steps |
| Distance covered at each stage | 4 m | 2.36 m | 2.6 m | 1.62 m |
| Total distance travelled after each stage | 4 m | 6.36 m | 8.96 m | 10.58 m |
Allow sufficient time for students to plan their journey. Group students into groups of three, appoint a captain for each team, and explain how the game works:
The captain is the master of the game. The other two students take turns asking him or her for permission to take a step along the way, for example, "Captain, will you let me do 8 frog jumps to move 4 metres forward?" At this point, the captain rolls a die and gives their answer based on the number on the die: if the number is 1, 2, 3, or 4, they accept; otherwise, they refuse.
If the request is accepted, the participant crosses the planned distance and indicates the total distance covered since the starting line. If the request is refused, they do not move and must wait until the next round to make the same request.
The captain is also responsible for checking the participant's calculations, using a calculator if necessary. If there is an error, the captain will order the participant to go back to the beginning.
The first person to cross the finish line (10 metres) wins.
The journey can be made by moving a counter on a ribbon, by marking distances on a number line or by actually making the journey. Allow enough time for students to play both roles (captain and participant).
Example
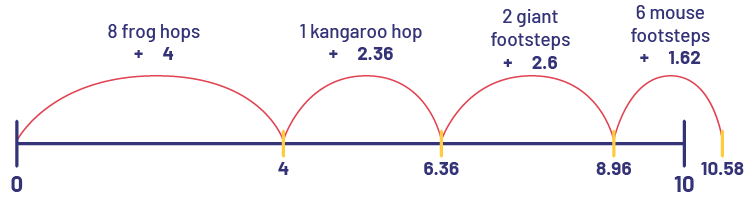
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 157-159.
