B2.6 Représenter et résoudre des problèmes relatifs à la multiplication d’un nombre naturel à deux chiffres par un nombre naturel à deux chiffres, et établir des liens entre la disposition rectangulaire et les algorithmes.
Activité 1 : cartes en folie
Écrire au tableau les chiffres : 0 1 2 3 4 5 6 7 8 9. À côté, écrire un nombre à 3 chiffres ou à 4 chiffres qui sera le nombre cible.
Exemple
876
5 210
Grouper les élèves par 2. Demander aux équipes de former, à partir des chiffres affichés, 2 nombres dont le produit se rapproche le plus possible du nombre cible (nombre à 3 chiffres ou à 4 chiffres). Les élèves peuvent seulement utiliser un chiffre 1 fois pour les 2 nombres. Il ne s’agit pas de viser une réponse exacte, mais d’estimer un résultat à l’aide de stratégies de calcul mental.
Exemples
\(\begin{array}{l}21\; \times \;40\; = \;840\\24\; \times \;36\; = \;864\\20\; \times \;43\; = \;860\end{array}\)
\(\begin{array}{l}61\; \times \;82\; = \;5\;002\\79\; \times \;65\; = \;5\;135\\78\; \times \;69\; = \;5\;382\end{array}\)
Suggérer aux équipes, pendant l’activité, d’expliquer et de comparer les résultats obtenus.
Il pourrait être intéressant de discuter de l’effet de l’arrondissement sur les opérations et des effets des opérations.
Source : adapté du Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 208.
Activité 2 : distributivité de la multiplication
Écrire au tableau chacune des séries d’opérations apparentées suivantes, 1 à la fois, et demander aux élèves d’effectuer les opérations qu’elle contient.
| Série 1 | Série 2 | Série 3 | Série 4 |
|---|---|---|---|
| \(\;3\; \times \;6\) | \(\;2\; \times \;13\) | \(\;4\; \times \;2\) | \(\;5\; \times \;5\) |
| \(\;3\; \times \;40\) | \(\;22\; \times \;10\) | \(4\; \times \;50\) | \(\;5\; \times \;30\) |
| \(\;3\; \times \;46\) | \(22\; \times \;3\) | \(\;4\; \times \;25\) | \(5\; \times \;100\) |
| \(\;20\; \times \;13\) | \(\;4\; \times \;77\) | \(\;5\; \times \;95\) | |
| \(\;22\; \times \;13\) |
Une fois une série complétée, faire ressortir les diverses stratégies de calcul mental en posant des questions telles que :
- Comment avez-vous résolu la dernière opération?
- Pour résoudre la dernière opération, avez-vous utilisé certains éléments des opérations précédentes?
- Avez-vous résolu les opérations dans l’ordre?
Si nécessaire, avant d’effectuer la même démarche avec la série suivante, présenter d’autres exemples d’opérations apparentées similaires.
Si les élèves ont de la difficulté à voir et à mettre en application la distributivité de la multiplication pour résoudre la dernière opération de chaque série, les y amener en représentant ces opérations sous forme de dispositions rectangulaires.
Exemple
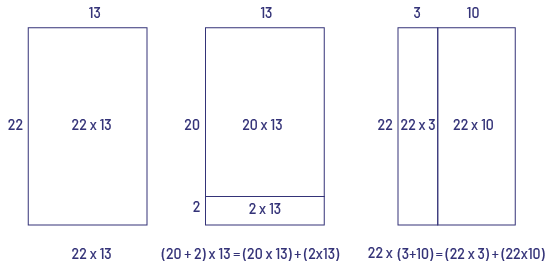image Un rectangle de 13 par 22, on obtient la multiplication 22 fois 13.Un rectangle divisé en 2 parties, la première est de 13 par 20 et la deuxième de 13 par 2. On obtient la phrase mathématique suivante :(parenthèse ouvrante) 20 plus 2 (parenthèse fermante) multiplié par 13, égal (parenthèse ouvrante) 20 multiplié par 13 (parenthèse fermante) plus (parenthèse ouvrante) 2 multiplié par 13 (parenthèse fermante).Un rectangle divisé en 2 parties, la première est de 3 par 22, et la deuxième est de 10 par 22. On obtient la phrase mathématique :22 multiplié par 3 (parenthèse ouvrante) 3 plus dix (parenthèse fermante) égal, (parenthèse ouvrante) 22 multiplié par 3 (parenthèse fermante) plus ( parenthèse ouvrante) 22 multiplié par dix (parenthèse fermante).
Constatations sur chacune des séries
Série 1
Cette série permet de revoir la propriété de distributivité de la multiplication sur l’addition à sa plus simple expression. Il s’agit de reconnaître que pour obtenir le produit de 3 × 46, il est possible d’effectuer une opération sur une somme de termes et d’obtenir le même résultat que si l’opération avait été effectuée sur chaque terme, c’est-à-dire :
\(3 \times 46 = 3 \times (40 + 6) \)
\(3 \times 46 = (3 \times 40) + (3 \times 6) \)
Série 2
Cette série permet de constater que la décomposition reliée à la distributivité peut s’effectuer aussi bien sur le 2e terme que sur le 1er, soit :
\(22 \times 13 = (20 \times 13) + (2 \times 13) \) ou
\(22 \times 13 = (22 \times 3) + (22 \times 10) \)
Série 3
Cette série permet de constater que la décomposition d’un nombre pour appliquer la distributivité peut se faire en plus de 2 parties. Par exemple :
\(4 \times 77 = 4 \times (50 + 25 + 2) \)
\(4 \times 77 = (4 \times 50 ) + (4 \times 25 ) + (4 \times 2 ) \)
Série 4
Cette série permet de constater que l’on peut résoudre la dernière opération à l’aide de la distributivité de la multiplication sur la soustraction.
\(5 \times 95 = 5 \times (100 - 5) \)
\(5 \times 95 = (5 \times 100 ) - (5 \times 5 ) \)
Elle permet aussi de constater que l’on peut résoudre cette opération à l’aide de la distributivité de la multiplication sur l’addition et d’autres propriétés.
\(5 \times 95 = 3 \times (5 \times 30) + (5 \times 5) \)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 221-222.
Activité 3 : le plus grand produit
Matériel
un dé
Rouler le dé 4 fois.
Noter les 4 nombres sur une feuille de papier. Créer un problème de multiplication qui aura le plus gros produit possible.
Exemples
Si je roule 2, 5, 6, 1, quelle multiplication aura le plus grand produit ? \(52\; \times \;61\;\;\;{\rm{ou}}\;\;\;{\rm{51}}\; \times \;{\rm{62}}\)
Si je roule 3, 3, 4, 3, quelle multiplication aura le plus grand produit? \(33\; \times \;34\;\;\;{\rm{ou}}\;\;\;{\rm{33}}\; \times \;\;4{\rm{3}}\)
Variante : Trouver le plus petit produit.
Source : adapté de L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).