B2.6 Represent and solve problems involving the multiplication of two-digit whole numbers by two-digit whole numbers using the area model and using algorithms, and make connections between the two methods.
Activity 1: Wild Cards
Write the digits 0 1 2 3 4 5 6 7 8 9 on the board. Write a 3-digit or 4-digit number next to them. This will be the target number.
Example
876
5210
Group students in pairs. Ask the teams to make two numbers using the digits displayed with products as close as possible to the target number (3-digit or 4-digit number) . Students can only use each digit once in their expressions. The goal is not to get an exact answer, but to estimate a result using mental math strategies.
Examples
\(\begin{array}{l}21\; \times \;40\; = \;840\\24\; \times \;36\; = \;864\\20\; \times \;43 \;=\;860\end{array}\)
\(\begin{array}{l}61\; \times \;82\; = \;5\;002\\79\; \times \;65\; = \;5\;135\\78\; \times \;69\; = \;5\;382\end{array}\)
Suggest that teams explain and compare their results during the activity.
It might be interesting to discuss the effect of rounding on operations and the effects of operations.
Source:adapted and translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 208.
Activity 2: Distributive Property of Multiplication
Write each of the following sets of related operations on the board, one at a time, and ask students to perform the operations in it.
| Set 1 | Set 2 | Set 3 | Set 4 |
|---|---|---|---|
| \(\;3\; \times \;6\) | \(\;2\; \times \;13\) | \(\;4\; \times \;2\) | \(\;5\; \times \;5\) |
| \(\;3\; \times \;40\) | \(\;22\; \times \;10\) | \(4\; \times \;50\) | \(5 \times 30\) |
| \(\;3\; \times \;46\) | \(22\; \times \;3\) | \(\;4\; \times \;25\) | \(5\; \times \;100\) |
| \(\;20\; \times \;13\) | \(\;4\; \times \;77\) | \(\;5\; \times \;95\) | |
| \(\;22\; \times \;13\) |
Once a set is completed, draw out the various mental math strategies by asking questions such as:
- How did you perform the last operation?
- To perform the last operation, did you use any of the previous operations?
- How would you describe the order in which you performed the operations?
If necessary, before doing the same with the next set, present other examples of similar related operations.
If students have difficulty seeing and applying the distributive property of multiplication over addition to calculate the last product in each set, suggest they represent these products as arrays.
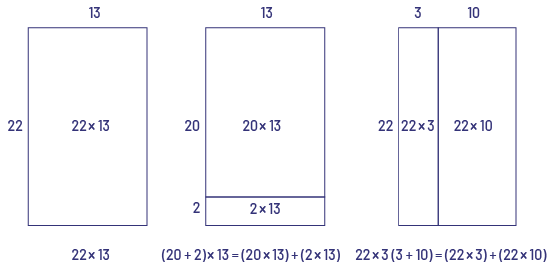
Example
Findings for each set
Set 1
This set allows us to review the distributive property of multiplication over addition in its simplest form. The aim is to recognize that, in order to obtain the product of 3 × 46, it is possible to perform an operation on a sum of terms and obtain the same result as if the operation had been performed on each term. For example:
\(3 \times 46 = 3 \times (40 + 6) \)
\(3 \times 46 = (3 \times 40) + (3 \times 6) \)
Set 2
This set allows us to see that the decomposition related to distributive property can be performed on the second term as well as on the first. For example:
\(22 \times 13 = (20 \times 13) + (2 \times 13) \) or
\(22 \times 13 = (22 \times 3) + (22 \times 10) \)
Set 3
This set shows that the decomposition of a number to apply the distributive property can be done in more than two parts. For example:
\(4 \times 77 = 4 \times (50 + 25 + 2) \)
\(4 \times 77 = (4 \times 50 ) + (4 \times 25 ) + (4 \times 2 ) \)
Set 4
This set allows us to see that we can solve the last operation using the distributive property of multiplication over subtraction. For example:
\(5 \times 95 = 5 \times (100 - 5) \)
\(5 \times 95 = (5 \times 100 ) - (5 \times 5 ) \)
It also shows that we can perform this operation using the distributive property of multiplication over addition and other properties.
\(5 \times 95 = 3 \times (5 \times 30) + (5 \times 5) \)
source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 221-222.
Activity 3: The Largest Product
Materials
a die
Roll the die four times.
Write the four numbers on a piece of paper. Create a multiplication computation that will have the largest possible product.
Example
If I roll 2, 5, 6, 1, which multiplication will have the greatest product? \(52\; \times \;61\;{\rm{or}}\;{\rm{51}}\; \times \;{\rm{62}}\)
If I roll 3, 3, 4, 3, which multiplication will have the greatest product? \(33\; \times \;34\;{\rm{or}}\;{\rm{33}}\; \times \;4{\rm{3}}\)
Variation: The smallest product.
Source: adapted and translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
