GEEM - Habiletés et connaissances

B2.3 Utiliser des stratégies de calcul mental pour multiplier des nombres naturels par 0,1 et 0,01 et estimer des sommes et des différences de nombres décimaux jusqu’aux centièmes, et expliquer les stratégies utilisées.

Habileté : utiliser des stratégies de calcul mental pour multiplier des nombres naturels par 0,1 et 0,01

Les élèves du cycle moyen ont déjà une expérience du concept de multiplication et comprennent que la multiplication de nombres naturels a pour effet de générer un produit supérieur aux quantités en cause, sauf dans les situations de multiplications par 1 et par 0. Il leur est alors souvent surprenant de constater qu’une multiplication dont l’un des facteurs est un nombre décimal inférieur à 1 donne un produit inférieur à l’autre facteur (par exemple, $10\; \times \;0,1\; = \;1\;\;\;{\rm{et}}\;\;\;{\rm{20}}\; \times \;{\rm{0}}\;{\rm{,10}}\;{\rm{ = }}\;{\rm{2}}$).

Ces résultats sont surprenants pour quiconque ne traite pas les nombres en contexte ou n’a pas acquis une compréhension de la multiplication lui permettant d’expliquer de tels résultats.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 79.

Lorsqu’on multiplie un nombre naturel par 0,1 la valeur devient 10 fois plus petite, qui est la même chose que diviser par 10.

Lorsqu’on multiplie un nombre naturel par 0,01, la valeur devient 100 fois plus petite, qui est la même chose que diviser par 100.

Multiplication effectuée à l’aide du tableau de valeur de position

Je visualise un déplacement de 1 colonne vers la droite dans le tableau de valeur de position.

$23\; \times \;0,1\; = \;2,3$

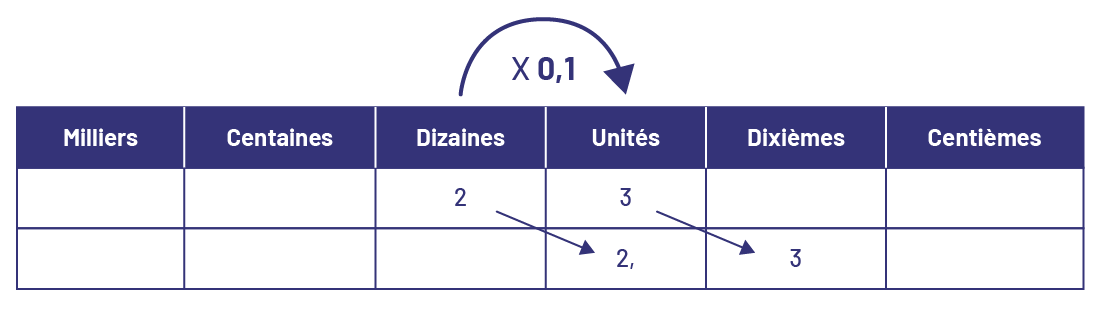
Tableau de position des valeursDe gauche à droite : milliers, centaines, dizaines, unités, dixièmes, centièmes.Une flèche indique le déplacement d’un nombre s’il est multiplié par zéro virgule un.2 dizaines devient 2 unités et 3 unités devient 3 dixièmes.

Je visualise un déplacement de 2 colonnes vers la droite dans le tableau de valeur de position.

$23\; \times \;0,01\; = \;0,23$

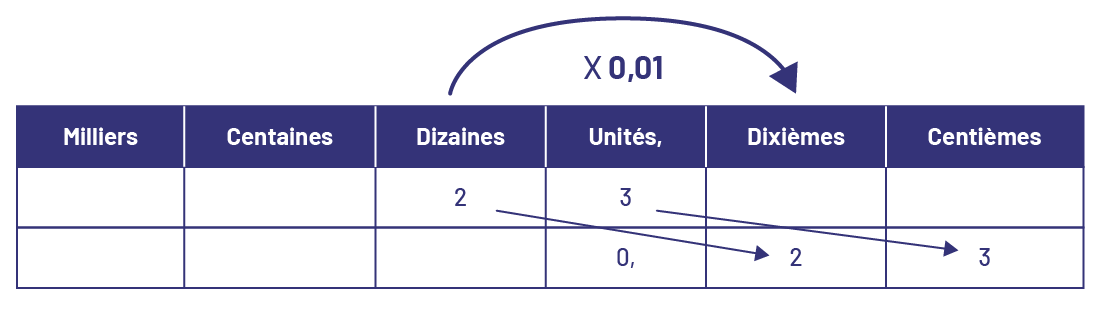
Multiplication effectuée à l’aide du matériel de base 10

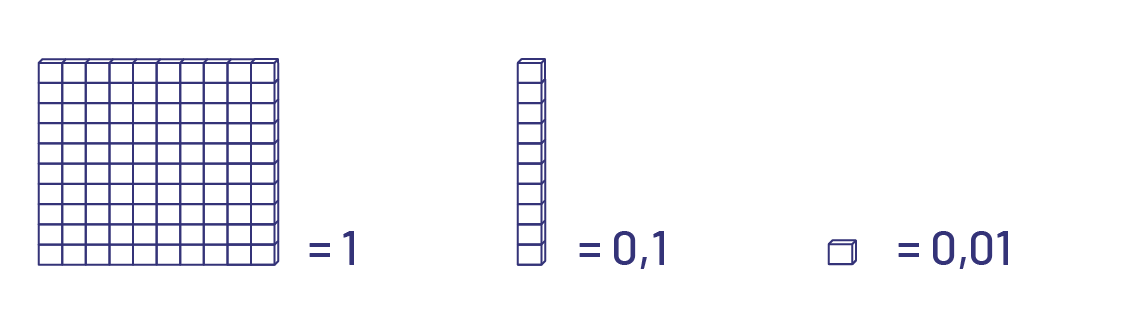
Une planchette de 100 cubes est égal à un.Une réglette de dizaine est égal à zéro virgule un.Un cube égal zéro virgule zéro un.

Exemple 1

$23\; \times \;0,1\; = \;2,3$

Pour effectuer $23\; \times \;0,1$, je visualise 23 bâtonnets.

Je sais qu’il me faut 10 bâtonnets pour faire une planchette. Je visualise un autre groupe de 10 bâtonnets. Il me reste 3 bâtonnets.

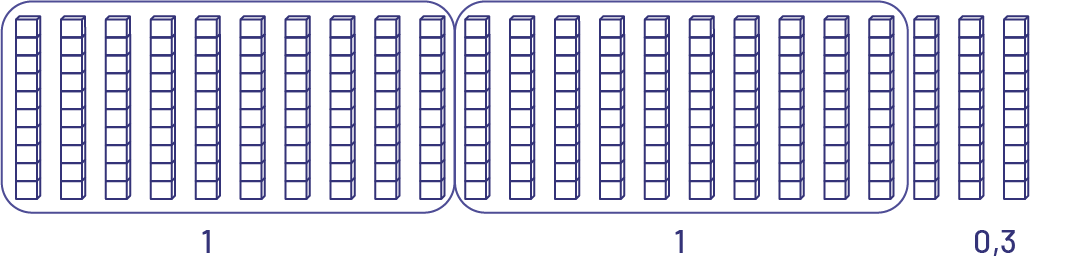
Deux ensembles de dix réglettes de dizaines, et 3 réglettes individuelles de dizaine. Chaque ensemble représente, un. Les 3 réglettes représentent, zéro virgule 3.

J’additionne mentalement les produits partiels : $1\, + \;1\; + \;0,3\; = \;2,3$

Exemple 2

$23\; \times \;0,01\; = \;0,23$

Pour effectuer $23\; \times \;0,01$, je visualise 23 petits cubes.

Je sais qu’il me faut 10 petits cubes pour faire un bâtonnet. Je visualise un autre groupe de 10 petits cubes. Il me reste 3 petits cubes.

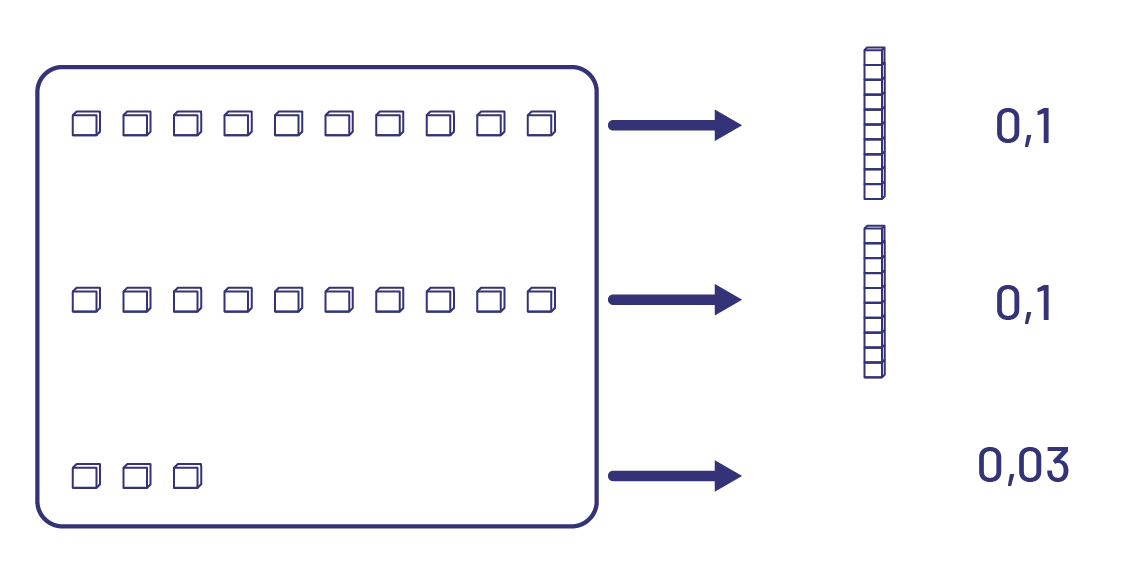
Dans un ensemble, 2 lignes de dix cubes et une ligne de 3 cubes.Chaque ligne de dix est égal à zéro virgule un. La ligne de 3 est égal à zéro virgule zéro 3.

J’additionne mentalement les produits partiels : $0,1\, + \;0,1\; + \;0,03\; = \;0,23$

Multiplication effectuée à l’aide de la division

Exemple 1

$23\; \times \;0,1\; = \;2,3$

Pour effectuer 23 × 0,1, je visualise le nombre 23 divisé en 10 groupes égaux. Je décompose 23 en 20 + 3.

$\begin{align}20\; \div \;10\; &= \;2\\3\; \div \;10\; &= \;0,3\\2\; + \;0,3\; &= \;2,3\end{align}$

Donc, dans chacun des groupes de 10, il y a 2,3.

Exemple 2

$23\; \times \;0,01\; = \;0,23$

Pour effectuer $23\; \times \;0,01$, je visualise le nombre 23 divisé en 100 groupes égaux. Je décompose 23 en 20 + 3.

$\begin{align}{l}20\; \div \;100\; &= \;0,20\\3\; \div \;100\; &= \;0,03\\0,20\; + \;0,03\; &= \;0,23\end{align}$

Donc, dans chacun des groupes de 100, il y a 0,23.

Source : adapté du CFORP, En avant, les maths!, 5^e année, ML, Nombres, p. 4-8.

Habileté : estimer des sommes et des différences de nombres décimaux jusqu’aux centièmes, et expliquer les stratégies utilisées

Pour additionner efficacement des nombres décimaux à l’aide de calcul mental, les élèves doivent comprendre la valeur de position des chiffres qui composent chacun des nombres et en tenir compte dans leurs calculs. Les élèves doivent aussi reconnaître que la virgule est un repère qui permet d’identifier la valeur de position des chiffres.

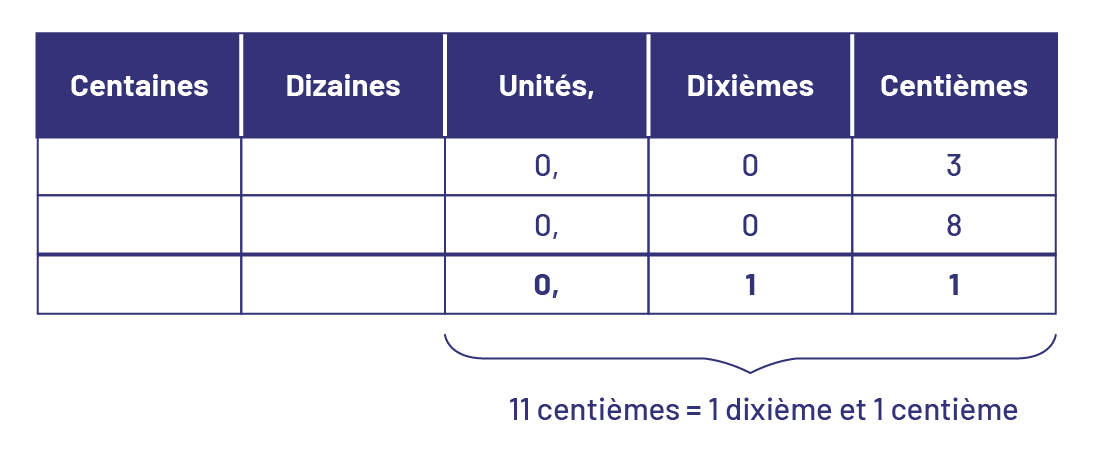
Lorsqu’on additionne des nombres décimaux, le concept de regroupement est utilisé tout comme lors de l’addition de nombres naturels. Par exemple, tout comme l’on peut ajouter 3 centaines à 8 centaines pour former 11 centaines, on peut ajouter 3 centièmes à 8 centièmes pour former 11 centièmes. Or, puisque le système décimal ne permet pas d’inscrire 2 chiffres dans une même position, les élèves doivent comprendre le concept de regroupement.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 98.

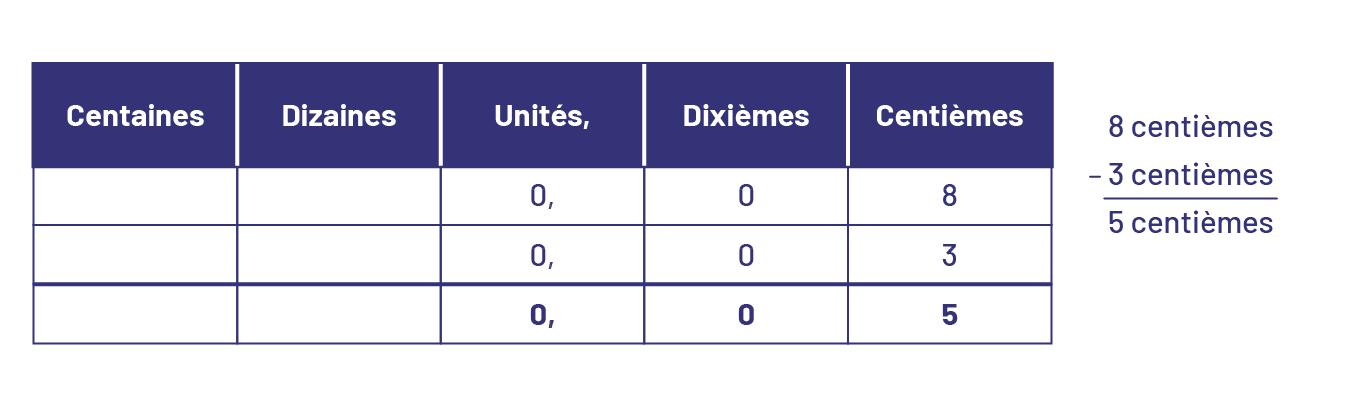
Au cours de la soustraction, il est important, comme il l’était dans le cas de l’addition, de tenir compte de la valeur de position des chiffres qui composent les nombres. Les stratégies pour soustraire les nombres décimaux sont essentiellement les mêmes que celles utilisées pour soustraire les nombres naturels. Par exemple, tout comme l’on peut soustraire 3 centaines de 8 centaines pour former 5 centaines, on peut soustraire 3 centièmes de 8 centièmes pour former 5 centièmes.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 101.

À l’aide de mots, il est plus facile d’effectuer la soustraction de 8 centièmes moins 3 centièmes. Ça donne 5 centièmes.

Calcul mental

La vie quotidienne présente de nombreuses occasions d’effectuer des opérations sur les nombres décimaux. Par exemple, les achats et les mesures font appel aux nombres décimaux. L’habileté à estimer et l’habileté à calculer mentalement sont des caractéristiques du sens du nombre et du sens des opérations. Diverses stratégies de calcul mental peuvent être utilisées dont l’arrondissement et l’utilisation de repères. Voici quelques exemples de leur utilisation en situation de calcul mental.

Arrondissement

Exemple 1

Annie doit acheter une douzaine d’œufs (2,77 $), un sac de 4 litres de lait (4,77 $), un pain (2,33 $), un melon (2,99 $) et un pot de sauce (3,65 $). Elle n’a que 20 $. A-t-elle assez d’argent?

Afin de savoir si elle a assez d’argent, elle peut :

arrondir les nombres au nombre naturel supérieur ($3\;\$ \; + \;5\;\$ \; + \;3\;\$ \; + \;3\;\$ \; + \;4\;\$ \; = \;18\;\$ $);
arrondir au dollar près ($3\;\$ \; + \;5\;\$ \; + \;2\;\$ \; + \;3\;\$ \; + \;4\;\$ \; = \;17\;\$ $);
arrondir au 0,50 $ près ($3\;\$ \; + \;5\;\$ \; + \;2,50\;\$ \; + \;3\;\$ \; + \;3,50\;\$ \; = \;17\;\$ $).

Chaque arrondissement effectué lui permet de conclure qu’elle a assez d’argent.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 91.

Exemple 2

La chienne de Casimir a donné naissance à 2 chiots. La vétérinaire explique que les chiots doivent peser au moins 22,75 kg lorsqu’ils ont 6 mois pour être en bonne santé. Casimir veut savoir combien de poids chaque chiot doit prendre. Le 1^er chiot pèse 3,23 kg et le 2^e chiot pèse 4,42 kg.

Afin de savoir combien de poids chaque chiot doit prendre, il peut arrondir les nombres au nombre naturel supérieur :

Chiot 1 $\left( {23\;\;{\rm{kg}}\; - \;{\rm{4}}\;\;{\rm{kg}}\;{\rm{ = }}\;{\rm{19}}\;\;{\rm{kg}}} \right)$

Chiot 2 $\left( {23\;\;{\rm{kg}}\; - \;5\;\;{\rm{kg}}\;{\rm{ = }}\;{\rm{18}}\;\;{\rm{kg}}} \right)$

L’arrondissement effectué lui permet de conclure que les chiots doivent augmenter de 19 kg et 18 kg.

Exemple 3

La classe de Carla veut acheter 6 pizzas qui coûtent 11,85 $ chacune (taxes incluses). Les élèves ont recueilli 71,50 $. Ont-elles et ils assez d’argent pour acheter les pizzas?

Afin de savoir si les élèves ont assez d’argent, le coût d’une pizza peut être arrondi à 12 $. Les élèves estiment alors le prix à environ 72 $ $\left( {6\; \times \;12\;\$ } \right)$.

Exemple 4

Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec l'addition de nombres décimaux.

Description de la vidéo

Description à venir

Utilisation de repères

Exemple

Afin d’estimer le coût de 4 jouets à 0,62 $ l’unité, on peut utiliser le nombre repère 0,50 $ et conclure que le coût s’élève à un peu plus de 2 $ $\left( {0,50\;\$ \; + \;0,50\;\$ \; + \;0,50\;\$ \; + \;0,50\;\$ \; = \;2\;\$ } \right)$.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 93.