B2.3 Use mental math strategies to multiply whole numbers by 0.1 and 0.01 and estimate sums and differences of decimal numbers up to hundredths, and explain the strategies used.
Skill: Using Mental Math Strategies to Multiply Whole Numbers by 0.1 and 0.01
Junior students already have experience with the concept of multiplication and understand that when multiplying whole numbers, we generate a product greater than either of the quantities involved, except in situations involving multiplication by 1 and by 0. They are often surprised to find that when multiplying two factors, if one of two factor is a decimal number less than 1, the product is less than the other factor (for example, \(10\; \times \;0.1\; = \;1\) and \(20 \times \;{\rm{0}}{\rm{.10}} = 2\)).
These results are surprising to anyone who has not deal with numbers in context or has not developed a conceptual understanding of multiplication that would explain such results.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 79.
When you multiply a whole number by 0.1 the value becomes one tenth as large, which is the same as dividing it by 10.
When you multiply a whole number by 0.01, the value becomes one one hundredth as large, which is the same as dividing it by 100.
Multiplication Performed Using the Place Value Chart
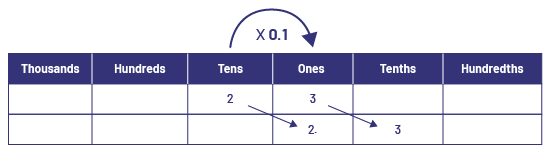
I visualized a shift of one column to the right in the place value chart.
\(23\; \times \;0.1\; = \;2.3\)
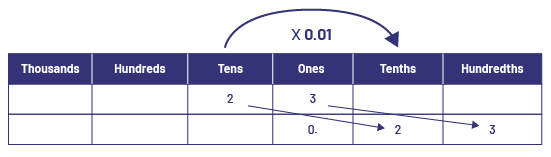
I visualized a shift of two columns to the right in the place value chart.
\(23\; \times \;0.01\; = \;0.23\)
Multiplication Using Base Ten Blocks
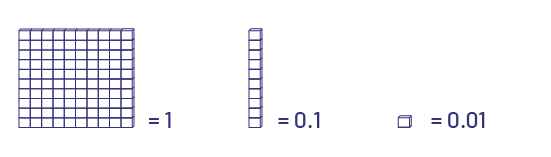
Example 1
\(23\; \times \;0.1\; = \;2.3\)
To calculate \(23\; \times \;0.1\), I visualized 23 rods.
I know I need 10 rods to make a flat, which is equal to one whole. I can visualize 2 groups of 10 rods, with 3 rods left over.
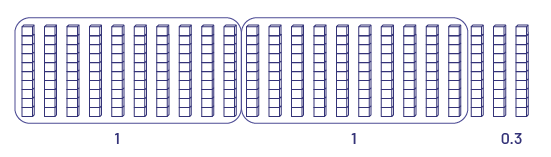
This is equal to \(1\, + \;1\; + \;0.3\; = \;2.3\)
Example 2
\(23\; \times \;0.01\; = \;0.23\)
To calculate \(23\; \times \;0.01\), I visualized 23 small cubes.
I know I need 10 small cubes to make a rod, which is equal to one tenth. I can visualize 2 groups of 10 small cubes with 3 small cubes left over.
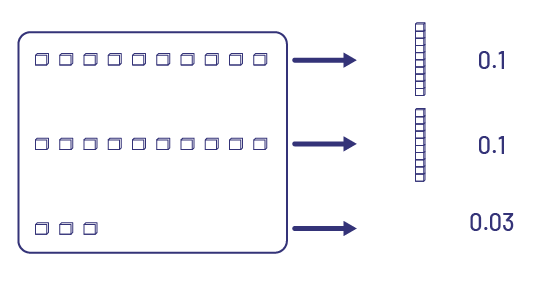
This is equal to \(0.1\, + \;0.1\; + \;0.03\; = \;0.23\)
Multiplication Using Division
Example 1
\(23\; \times \;0.1\; = \;2.3\)
Multiply by one tenth is the same as dividing by 10. So to calculate 23 × 0.1, I visualized the number 23 divided into 10 equal groups. I decomposed 23 into 20 + 3.
\(\begin{array}{l}20\; \div \;10\; = \;2\\3\; \div \;10\; = \;0.3\\2\; + \; 0.3\;=\;2.3\end{array}\)
The answer is 2.3.
Example 2
\(23\; \times \;0.01\; = \;0.23\)
Multiply by one hundredth is the same as dividing by 100. So to calculate \(23\; \times \;0.01\), I visualized the number 23 divided into 100 equal groups. I decomposed 23 into 20 + 3.
\(\begin{array}{l}20\; \div \;100\; = \;0.20\\3\; \div \;100\; = \;0.03\\0.20\;+\;0.03\;=\;0.23\end{array}\)
The answer is 0.23.
Source: Adapted and translated from En avant, les maths, 5e, ML, Nombres, pp. 4-8.
Skill: Estimating Sums and Differences of Decimal Numbers to Hundredths, and Explaining the Strategies Used
To add decimal numbers effectively using mental math, students need to understand the place value of the digits that make up each number and factor that into their calculations. Students should also recognize that the decimal point is a marker that identifies the place value of the digits.
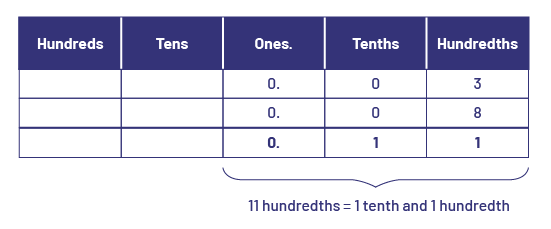
When adding decimal numbers, the concept of grouping is used just as when adding whole numbers. For example, just as we can add 3 hundreds to 8 hundreds to form 11 hundreds, we can add 3 hundredths to 8 hundredths to form 11 hundredths. However, since the decimal system does not allow two digits to be placed in the same position, students must understand the concept of regrouping.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 98.
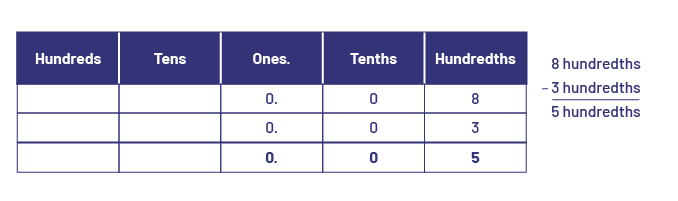
During subtraction, it is important, as it is with addition, to consider the place value of the digits that make up the numbers. The strategies for subtracting decimal numbers are essentially the same as those used for subtracting whole numbers. For example, just as one can subtract 3 hundreds from 8 hundreds and get 5 hundreds, one can subtract 3 hundredths from 8 hundredths to get 5 hundredths.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 101.
Mental Math
Daily life presents many opportunities to perform operations with decimal numbers. For example, shopping and measuring can involve decimal numbers. Estimation skills and mental math skills are important elements of number and operation sense. A variety of mental math strategies can be used including rounding and the use of benchmarks. Below are some examples of their use in mental math situations.
Rounding
Example 1
Annie needs to buy a dozen eggs ($2.77), a 4-litre bag of milk ($4.77), a loaf of bread ($2.33), a melon ($2.99), and a jar of sauce ($3.65). She only has $20. Does she have enough money?
To find out if she has enough money, she can:
- round numbers up to the nearest whole number (\(\$3 \; +\; \$5 \;+\; \$3 \;+\; \$3 \;+ \$4\;=\;\$18\));
- round to the nearest dollar (\(\$3\; + \;\$5\; + \;\$2\; + \;\$3\; +\; \$4 \;= \;\$17\));
- round to the nearest $0.50 (\(\$3\; +\; \$5 \;+\; \$2.50 \;+\; \$3\; + \;\$3.50\; =\; \$17\)).
With each rounding, she concludes that she has enough money.
source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 91.
Example 2
Casimir's dog gave birth to 2 puppies. The vet explains that puppies must weigh at least 22.75 kg when they are 6 months old to be considered healthy. Casimir wants to know how much weight each puppy should gain. The 1st puppy weighs 3.23 kg and the 2nd puppy weighs 4.42 kg.
In order to know how much weight each puppy should gain, he can round the numbers up to the nearest whole number:
Puppy 1 \(\left( {23\;{\rm {kg}}\; - \;{\rm{4}}\;{\rm {kg}}\;{\rm{ = }}\; {\rm{19}}\;{\rm {kg}}} \right)\)
Puppy 2 \(\left( {23\;{\rm {kg}}\; - \;5\;{\rm {kg}}\;{\rm{ = }}\;{\rm{18} }\;{\rm {kg}}} \right)\)
After rounding, he concludes that the puppies should increase by 19 kg and 18 kg respectively.
Example 3
Carla's class wants to buy 6 pizzas that cost $11.85 each (tax included). The students have raised $71.50. Do they have enough money to buy the pizzas?
To determine if students have enough money, the cost of a pizza can be rounded up to $12. The students then estimate the price at around $72 \(\left( {6\; \times $\;12 } \right)\).
Use of Benchmarks
Example
In order to estimate the cost of 4 toys at $0.62 each, we can use the benchmark number $0.50 and conclude that the cost amounts to a little over $2 \(\left( {\$0.50 \;+ \;\$0.50\; +\; \$0.50 \;+\; \$0.50 \;=\; \$2 } \right)\).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 93.
