B2.7 Représenter et résoudre des problèmes relatifs à la division d’un nombre naturel à trois chiffres par un nombre naturel à deux chiffres, et établir des liens entre la disposition rectangulaire et les algorithmes, et exprimer le reste de façon appropriée.
Habileté : résoudre des problèmes de division d’un nombre naturel à 3 chiffres par un nombre naturel à 2 chiffres
Les élèves acquièrent une bonne compréhension de la multiplication et de la division ainsi que des relations entre les nombres en résolvant des problèmes écrits. Les types de problèmes présentés ci-après à l’aide d’exemples peuvent aider les élèves à percevoir les faits numériques de base relatifs à la multiplication et à la division de diverses façons, selon qu’il s’agit de problèmes de groupes égaux et de comparaison. Le recours aux problèmes pour présenter les faits numériques de base oblige les élèves à raisonner pour trouver des solutions et permet ainsi de développer un meilleur sens des opérations.
Les exemples de problèmes écrits ci-dessous contiennent des nombres d’un chiffre. Les structures des 2 types de problèmes écrits se prêtent aussi aux nombres à plusieurs chiffres.
Groupes égaux : nombre de groupes inconnu (groupement)
L’école a acheté 150 livres pour les classes et prépare des bacs. Un parent bénévole met 30 livres dans chaque bac. Combien de bacs le parent a-t-il utilisés?
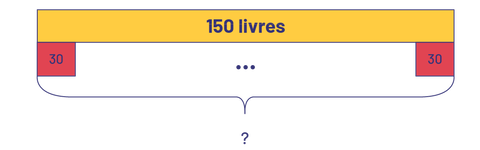image Un rectangle jaune représente 150 livres. En dessous 2 carrés rouges représentent 30. Un espace vide est entre les 2 carrés rouges. L’espace vide plus les carrés rouges représentent une inconnue.150 divisé par 30 égal une inconnue.Ou une inconnue fois 30 égal 150.
\(\) \({\rm{150}}\; \div \;30\;{\rm{ = }}\;?\;\;\;{\rm{ou}}\;\;\;?\; \times \;30\; = \;150\;\)
La disposition rectangulaire
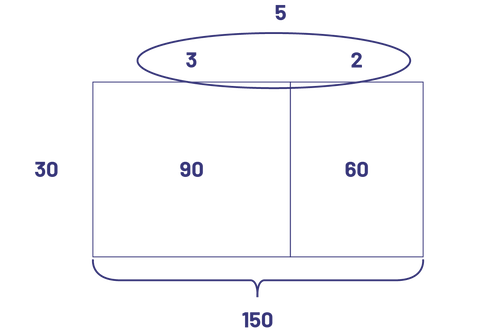image Une disposition rectangulaire, la longueur est de 3 plus 2 pour un total de 5, et de 30 sur la largeur. Les 2 rectangles qui sont dans la disposition représentent 90 et 60 pour un total de 150.
Le parent bénévole a utilisé 5 bacs pour les livres.
Groupes égaux : taille des groupes inconnue (partage)
L’école achète 150 livres pour chacune des 5 classes. Un parent bénévole prépare 5 bacs de livres. Combien de livres chaque bac contient-il?
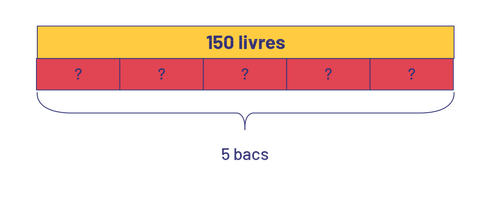image Un rectangle jaune représente 150 livres. En dessous il y a 5 rectangles plus petits, qui représentent 5 bacs.150 divisé par 5 égal une inconnue. Ou, 5 fois une inconnue égal 150.
\({\rm{150}}\; \div \;5\;{\rm{ = }}\;?\;\;\;{\rm{ou}}\;\;\;5\; \times \;?\; = \;150\;\)
Un partage
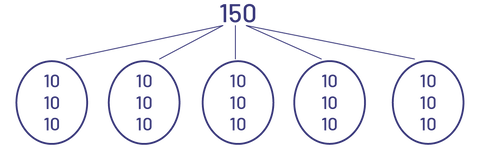
\(10\; + \;10\; + \;10\; = \;30\)
Chaque bac contient 30 livres.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10-11.
La notion du reste
Dans une division, le concept de reste survient lorsque le quotient n’est pas un nombre entier. Par exemple, \(10\; \div \;3\; = \;3,33 \ldots \) ou 3 reste 1. Pour plusieurs élèves, le reste n’est qu’un nombre qui paraît dans la « recette » de la division (par exemple, \(123\; \div \;5\; = \;24\;\;\;{\rm{reste}}\;\;\;{\rm{3}}\)).
Cependant, lorsque l’opération surgit d’un contexte, le reste doit être traité afin de pouvoir répondre adéquatement au problème. Ainsi, les élèves peuvent développer l’habileté à traiter le reste s’ils sont en situation de résolution de problèmes. Le tableau ci-après présente plusieurs façons de traiter le reste.
Divers traitements du reste
| Traitement du reste | Exemple de problème |
|---|---|
| Le reste est réparti équitablement et exprimé sous la forme d’un nombre décimal. | Lors d’un tirage à leur club d’auto, 4 amis ont gagné le gros lot de 3 457 $ qu’ils se sont partagés également. Quel montant chaque personne a-t-elle reçu? \(3\;457\; \div \;4\; = \;864\;\;\;{\rm{reste}}\;\;\;{\rm{1}}\) Exemple de réponse : Chaque personne a reçu 864,25 $ |
| Le reste est réparti équitablement et exprimé sous la forme d’une fraction. | Une grand-maman achète un sac de 35 réglisses pour ses 3 petits-enfants. Si chaque enfant en reçoit le même nombre, combien de réglisses chacun reçoit-il?
\(35\; \div \;3\; = \;11\;\;\;{\rm{reste}}\;\;\;2\) Exemple de réponse : Chaque enfant reçoit \(11\frac{2}{3}\) réglisses. |
| Le reste est ignoré. | Daniel, Sophia, Ahmed et Franco ont un total de 3 458 blocs pour construire un château. Si chacun reçoit le même nombre de blocs, combien chacun en reçoit-il?
\(3\;458\; \div \;4\; = \;864\;\;\;{\rm{reste}}\;\;\;2\) Exemple de réponse : Chacun reçoit 864 blocs. |
| Le reste est réparti parmi les groupes. | M. Buzini veut que les élèves accomplissent une tâche en groupes de 2. Il a 23 élèves. Comment organisera-t-il ses élèves?
\(23\; \div \;2\; = \;11\;\;\;{\rm{reste}}\;\;\;1\) Exemple de réponse : Il formera 10 groupes de 2 élèves et 1 groupe de 3 ou 11 groupes de 2 élèves et un élève travaille seul. |
| Le reste entraîne la majoration du quotient de 1. | La directrice d’une école veut emmener tous les élèves lors d’une sortie éducative. Il y a 587 élèves dans l’école et il est possible d’accommoder un maximum de 72 élèves par autobus. Combien d’autobus doit-on réserver?
\(587\; \div \;72\; = \;8\;\;\;{\rm{reste}}\;\;\;11\) Exemple de réponse : On doit réserver 9 autobus. |
| Le reste est la réponse. | À la foire, les organisateurs décident de remettre gratuitement 350 billets pour les manèges aux premiers visiteurs à raison de 4 billets par visiteur. Combien de billets n’ont pas été remis?
\(350\; \div \;4\; = \;87\;\;\;{\rm{reste}}\;\;\;2\) Exemple de réponse : Deux billets n’ont pas été remis. |
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 86-87.
Divisions de nombres à plusieurs chiffres
(Van de Walle et Folk, 2005, p. 200)
Il est également important de présenter aux élèves la division dans un contexte de résolution de problèmes. Il y a principalement deux sortes de problèmes de division : ceux associés à la soustraction répétée et ceux associés au partage ou à la répartition égale. Il est important que les élèves soient confrontés aux deux types de problèmes et qu’ils utilisent leurs propres stratégies pour les résoudre.
Exemple de problème associé à la soustraction répétée
Mme Langlois a 226 gommettes. Tous les jours, elle donne 35 gommettes à ses élèves. Au bout de combien de jours Mme Langlois aura-t-elle donné toutes ses gommettes?
Pour résoudre ce problème, les élèves peuvent soustraire successivement 35 gommettes en prenant soin de garder un compte du nombre de soustractions effectuées.
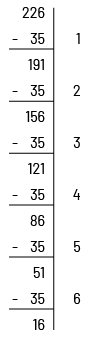
Ils pourront alors conclure que Mme Langlois sera en mesure de donner des gommettes pendant 6 jours et qu’il lui restera 16 gommettes (226 ÷ 35 = 6, reste 16).
Exemple de problème associé au partage ou à la répartition égale
Annick a 652 ballons qu’elle veut donner à 15 de ses amies. Combien de ballons recevra chaque amie?
Les problèmes de partage se prêtent bien à l’utilisation du matériel de base dix parce que cela permet aux élèves de visualiser le partage et de développer une compréhension de l’algorithme usuel de la division. Pour résoudre le problème, les élèves représentent d’abord le nombre 652 en plaçant sur leur pupitre 6 centaines (planchettes), 5 dizaines (languettes) et 2 unités (cubes d’unité).
Puisqu’il est impossible de partager 6 centaines (planchettes) entre 15 amies, les centaines sont alors échangées contre dix dizaines chacune, ce qui fait un total de 65 dizaines.
image 6 planchettes de centaines, sous chaque planchette une flèche pointe vers le bas où 10 réglettes de dizaines sont placées en groupes de 5.Il y a donc un total de 60 réglettes de dizaines, sous les planchettes, plus 5 autres réglettes de dizaines sur le côté.
Les dizaines sont réparties parmi les 15 amies, ce qui fait 4 dizaines (40) ballons chacune. Il reste 5 dizaines.
image 13 ensembles de 5 réglettes de dizaines sont disposés sur 2 rangées. Des ensembles de 4 réglettes de dizaines sont formés. Il reste 5 dizaines à part. Une flèche pointe vers le bas, Les réglettes de dizaines sont maintenant placés en 16 connes. 15 colonnes forment 15 ensembles de 4 réglettes de dizaines, et une colonne a 5 réglettes de dizaines.
Il reste ensuite à partager les 5 dizaines et les 2 unités restantes entre les 15 amies. Les 5 dizaines sont échangées pour 50 unités afin de pouvoir procéder au partage.
image 5 réglettes de dizaines et 2 unités sont divisées en groupes de dix unités individuelles. Ces unités sont en ensemble de 3. Il reste pour chaque groupe une unité et il y a 2 unités sur le côté qui ne font pas partie d’un groupe de dix. On obtient une disposition de 15 colonnes de 3 blocs d’unités, et un groupe de 7 blocs d’unités.
Les 7 unités qui restent ne peuvent pas être partagés en parts égales entre les 15 amies.
Les élèves peuvent alors conclure que chaque amie recevra 43 ballons (4 dizaines et 3 unités) et qu’il restera 7 ballons (652 ÷ 15 = 43, reste 7).
Cette modélisation permet aux élèves de visualiser le partage et de construire une compréhension conceptuelle de la division. Le personnel enseignant peut aider les élèves à faire des liens entre le partage du matériel de base dix et les étapes de l’algorithme usuel de la division.
« Peut-on diviser également les centaines?»
On ne peut pas diviser également les centaines en 15 groupes.
« Si on échange les 6 centaines pour 60 dizaines, combien de dizaines aurons-nous? »
Nous aurons 65 dizaines.
« Peut-on diviser également les dizaines? Combien doit-on en placer dans chaque groupe? »
« Si on échange les dizaines qui restent pour 50 unités, combien d’unités aurons-nous? »
« Peut-on diviser également les unités? »
Une autre façon d’effectuer la division est de recourir à une somme de quotients partiels fondés sur ses connaissances antérieures. Cette stratégie a l’avantage de développer le sens de l’ordre de grandeur des nombres. Par exemple, pour partager les 652 ballons, les élèves peuvent d’abord reconnaître qu’il est possible de distribuer 10 ballons à chacune des 15 amies. Ils calculent alors que ce partage correspond à distribuer 150 ballons et qu’il en restera 502.
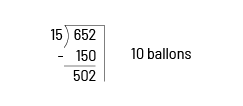
Puisqu’il reste un plus grand nombre de ballons que ce qu’ils viennent de distribuer, ils peuvent choisir de doubler la prochaine estimation à 20 ballons. Ceci correspond à distribuer 300 autres ballons. Il en reste maintenant 202.
Il est encore possible de distribuer 10 ballons à chaque amie, pour un autre 150 ballons. Il reste maintenant 52 ballons.
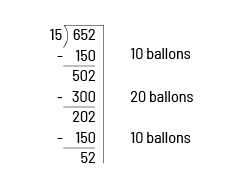
Finalement, ils peuvent conclure qu’il est encore possible de distribuer 3 ballons à chaque amie, pour un total de 45 ballons, et qu’il restera 7 ballons. Au total, on a donc distribué 10+20+10+3=43 ballons.
image 15 divise (parenthèse ouvrante) 652 moins 150 égal 502, moins 300 égal 202, moins 150 égal 52, moins 45 égal 7 (parenthèse fermante). 150 pour dix ballons, 300 pour 20 ballons, 45 pour 3 ballons.10 ballons, plus 20 ballons, plus 10 ballons, plus 3 ballons, égal 43 ballons, reste 7.
Cette démarche permet à l’élève d’effectuer une division à partir de ce qu'il connaît. Même si la démarche de l’élève a plusieurs étapes, elle permet en général d’éliminer les erreurs de calcul puisqu’elle ou il utilise des calculs connus.
Source : adapté de Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 65-68.
Il importe aussi que les élèves aient vu plusieurs notations de la division afin de pouvoir facilement passer de l’une à l’autre et d’élargir leur banque de stratégies personnelles. Par exemple, pour exprimer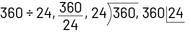 
image 360 divisé par 24.360 sur 24.Division qui utilise la représentation nord-américaine où le diviseur, 24, est à gauche et le dividende, 360, est dans un encadré.Division forme posée ou le dividende, 360, est à gauche et le diviseur, 24 est dans l’encadré. , il arrive que des élèves ignorent où positionner le dividende, le diviseur et le quotient. Cette situation se produit moins souvent si l’algorithme émane des élèves, car elles et ils comprennent mieux ce qui se passe.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 145.
Connaissance : types de division
Il existe 2 types de problèmes de division. Les autres découlent de la multiplication.
Le type « groupement »
Ici, on connaît le nombre total d’objets et le nombre d’objets dans chaque groupe. On cherche le nombre de groupes.
Le type « partage »
Ici, on partage un ensemble d’objets également entre un certain nombre de groupes ou de personnes. On connaît le nombre total d’objets et le nombre de groupes. On cherche le nombre d’objets dans chaque groupe.