B2.7 Represent and solve problems involving the division of three-digit whole numbers by two-digit whole numbers using the area model and using algorithms, and make connections between the two methods, while expressing any remainder appropriately.
Skill: Solving Problems Involving Division of Three-Digit Whole Numbers by Two-Digit Whole Numbers
Students develop an understanding of multiplication and division and the relationships between numbers by solving problems. The types of problems with examples presented below can support students to see basic multiplication and division facts in a variety of ways, depending on whether the problems are equal groups or comparison problems. Using problems to introduce basic number facts promotes students to reason their way to solutions and thus develops a better sense of operations.
The sample written problems below contain one-digit numbers. The structures of both types of written problems also lend themselves to multi-digit numbers.
Equal-Sharing: Number of Groups Unknown (Quotative Division)
The school has purchased 150 books for the classrooms and is sorting them into bins. A parent volunteer puts 30 books in each bin. How many bins did the parent use?
\(\) \({\rm{150}}\; \div \;30\;{\rm{ = }}\;?\;{\rm{or}}\;?\; \times \;30\; = \;150\;\)
The Array
The parent volunteer used 5 bins for books.
Equal-Sharing: Group Size Unknown (Partitive Division)
The school purchases 150 books for each of the 5 classes. A parent volunteer prepares 5 bins of books. How many books does each bin contain?
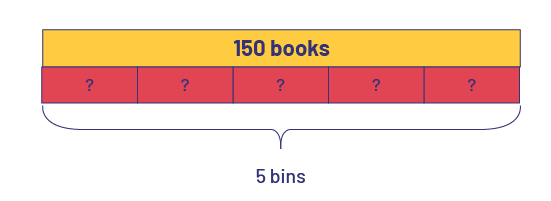
\({\rm{150}}\; \div \;5\;{\rm{ = }}\;?\;{\rm{or}}\;5\; \times \;?\; = \;150\;\)
Sharing (Partitive)
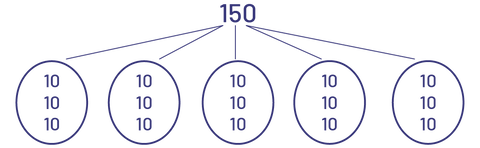
\(10\; + \;10\; + \;10\; = \;30\)
Each bin contains 30 books.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 10-11.
The Concept of Remainder
In division, the concept of remainder arises when the quotient is not a whole number. For example, \(10\; \div \;3\; = \;3.33 \ldots \) or 3 remainder 1. For many students, the remainder is just a number that appears in the "recipe" of the division (for example, \(123\; \div \;5\; = \;24\;{\rm {remainder} }\;{\rm{3}}\)).
However, when the operation arises from a context, the remainder must be considered in order to adequately answer to the problem. Thus, students can develop the ability to deal with the remainder when working through a problem-solving situation. Here are several ways to process the remainder:
Ways the remainder might be treated
| Treatment of the Remainder | Examples of Problems |
|---|---|
| The remainder is distributed equally and expressed as a decimal number. | In a draw at their car club, 4 friends won the grand prize of $3457, which they shared equally. How much did each friend receive? \(3457\; \div \;4\; = \;864\;{\rm{R}}\;{\rm{1}}\) Sample Answer: Each person received $864.25 |
| The remainder is divided equally and expressed as a fraction. | A grandmother buys a bag of 35 licorice chews for her 3 grandchildren. If each child gets the same number of licorice chews, how many does each child get?
\(35\; \div \;3\; = \;11\;{\rm{R}}\;2\) Sample answer: Each child receives \(11\frac{2}{3}\) licorice. |
| The remainder is ignored. | Daniel, Sophia, Ahmed and Franco have a total of 3458 blocks to build a castle. If each gets the same number of blocks, how many does each get?
\(3\;458\; \div \;4\; = \;864\;{\rm{R}}\;2\) Sample answer: Each receives 864 blocks. |
| The rest is distributed among the groups. | Mr. Buzini wants students to complete a task in groups of 2. He has 23 students. How will he organize his students?
\(23\; \div \;2\; = \;11\;{\rm{R}}\;1\) Sample answer: He will form 10 groups of 2 students and 1 group of 3 or 11 groups of 2 students and one student works alone. |
| The remainder increases the quotient by 1. | The principal of a school wants to take all the students on a field trip. There are 587 students in the school and a maximum of 72 students can be accommodated per bus. How many buses should be reserved?
\(587\; \div \;72\; = \;8\;{\rm{R}}\;11\) Sample answer: We need to reserve 9 buses. |
| The remainder is the answer. | At the fair, the organizers decide to give out 350 free tickets at a rate of 4 tickets per visitor. How many tickets were left over?
\(350\; \div \;4\; = \;87\;{\rm{R}}\;2\) Sample response: Two tickets were not given out. |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 86-87.
Dividing Multi-Digit Numbers
(Van de Walle and Folk, 2005, p. 200)
It is also important to introduce students to division in a problem-solving context. There are mainly two kinds of division problems: those associated with repeated subtraction and those associated with sharing or equal distribution. It is important that students are confronted with both types of problems and that they use their own strategies to solve them.
Example of a Division Problem Associated With Repeated Subtraction
Mrs Langlois has 226 stickers. Every day, she gives 35 stickers to her students. After how many days will Mrs Langlois have given out all her stickers?
To solve this problem, students can successively subtract 35 stickers, taking care to keep track of the number of subtractions made.
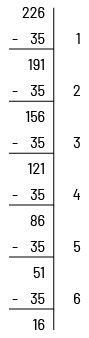
They will then be able to conclude that Mrs. Langlois will be able to give stickers for 6 days and that she will have 16 stickers left (226 ÷ 35 = 6 R16).
Example of a Problem Associated With Sharing or Equal Distribution
Annick has 652 balloons that she wants to give to 15 of her friends. How many balloons will each friend receive?
Sharing problems lend themselves well to the use of base ten blocks because they allow students to visualize sharing and develop a conceptual understanding of what is happening in the standard division algorithm. To solve the problem, the students first represent the number 652 with 6 hundreds (flats), 5 tens (rods) and 2 ones (small cubes).
Since it is impossible to share 6 hundreds (flats) among 15 friends, the hundreds are exchanged for 10 tens each, for a total of 65 tens.
The tens are distributed among the 15 friends, who will each receive 4 tens (40) balloons. There are 5 tens left.
The remaining 5 tens and 2 ones must then be shared among the 15 friends. The 5 tens are exchanged for 50 ones in order to proceed with the sharing.
The remaining 7 ones cannot be shared equally among the 15 friends.
Students can then conclude that each friend will receive 43 balloons (4 tens and 3 ones) and that 7 balloons are left over and will not be shared (652 ÷ 15 = 43 R7).
This modelling allows students to visualize sharing and build a conceptual understanding of division. Teachers can help students make connections between sharing using the base ten blocks and the steps in the standard division algorithm.
Can we divide the hundreds equally?
The hundreds cannot be divided equally into 15 groups.
If we exchange the six hundreds for 60 tens, how many tens will we have?
We will have 65 tens.
Can we divide the 65 tens equally? How many tens can each group get?
Now we have 5 tens, which is the same as 50 ones, and the remaining 2 ones.
Now we think about how many of the 52 ones each group will get.
Another way to do division is to use a sum of partial quotients based on prior knowledge. This strategy has the advantage of developing a sense of the relative size of numbers. For example, to divide the 652 balloons, students may first recognize that it is possible to distribute 10 balloons to each of 15 friends. They then calculate that this will result in the distribution of 150 balloons and that there will be 502 left.
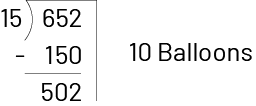
Since there are more balloons left than they just handed out, they can choose to double the next estimate to 20 balloons. This is equivalent to giving out another 300 balloons. There are now 202 balloons left.
It is still possible to distribute 10 balloons to each friend, for another 150 balloons. There are now 52 balloons left.
Finally, they can conclude that it is still possible to distribute 3 balloons to each friend, for a total of 45 balloons, and that 7 balloons will remain. In total, 10+20+10+3=43 balloons.
This approach allows the student to perform division based on what they know. Although this approach has several steps, it generally eliminates calculation errors since students are using known calculations.
Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 65-68.
It is also important for students to have seen several ways of expressing division so that they can easily switch from one to another and expand their bank of personal strategies. For example, when expressing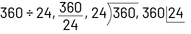 
some students may not know where to place the dividend, divisor and quotient. This situation occurs less often if the algorithm comes from the students, as they have a better understanding of what is happening.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 145.
Knowledge: Types of Division
There are two types of division problems. The others are derived from multiplication.
The "Equal-Grouping" Division (Quotative Division)
Here we know the total number of objects and the number of objects in each group. We are looking for the number of groups.
The "Equal-Sharing" Division (Partitive Division)
Here, a set of objects is divided equally among a number of groups or individuals. We know the total number of objects and the number of groups. We look for the number of objects in each group.