B2.8 Multiplier et diviser un nombre naturel à un chiffre par une fraction unitaire, à l’aide d’outils et de schémas.
Habileté : multiplier un nombre naturel à un chiffre par une fraction unitaire
Au cycle moyen, les élèves ont déjà un bagage de connaissances sur la multiplication. En effet, depuis le cycle primaire, elles et ils explorent des concepts reliés à la multiplication à l’aide de matériel concret, de la calculatrice, d’illustrations et de symboles. En 4e année, la multiplication de fractions est limitée à la multiplication d’un nombre naturel à un chiffre par une fraction unitaire. Ce type de multiplication peut être compris en le reliant à l’addition répétée. Ainsi, les élèves saisissent facilement que \(3\; \times \;\frac{1}{2}\), qu’on peut lire « 3 fois 1 demi », est une multiplication qui peut être représentée par l’addition répétée, soit \(\frac{1}{2}\; + \;\frac{1}{2}\; + \;\frac{1}{2}\). Elles doivent être explorées pour aider les élèves à comprendre la multiplication des fractions.
Cependant, il est plus difficile de donner un sens à la multiplication d’une fraction par un nombre naturel (par exemple, \(\frac{1}{2}\; \times \;3\)). Ces situations sont explorées à partir de la 5e année. Il existe un lien entre le concept de multiplication d’une fraction et celui de fraction d’un ensemble. La fraction d’un ensemble est un concept relié au concept de fraction. Par exemple, en 2e année, les élèves apprennent le sens de \(\frac{1}{2}\), \(\frac{1}{4}\) et \(\frac{1}{3}\) d’un groupe contenant jusqu'à 10 objets. Plus tard, elles et ils consolident leur compréhension du concept de fraction d’un ensemble en l’appliquant à d’autres fractions. En 5e année, en examinant le concept de multiplication d’une fraction unitaire par un nombre naturel à un chiffre, elles et ils apprendront que la fraction d’un ensemble (\(\frac{1}{3}\)de 6) est reliée à la multiplication et que cette situation peut être représentée par une multiplication (\(\frac{1}{3}\; \times \;6\)).
Les mathématiciennes et les mathématiciens ont décidé qu’il s’agissait d’une multiplication en procédant à peu près comme suit :
- on peut considérer \(4\; \times \;6\) comme 4 groupes de 6;
- on peut considérer \(2\; \times \;8\) comme 2 groupes de 8.
On n’a aucune difficulté à étendre ce constat à des nombres fractionnaires supérieurs à 2 :
- on peut considérer \(4 \frac{1}{2}\; \times \;6\) comme 4 groupes et demi de 6;
- on peut considérer \(2\frac{1}{3}\; \times \;12\) comme 2 groupes et un tiers de 12.
On généralise cette situation (ce qui implique une abstraction, puisque le groupe n’est pas « multiplié » comme tel) en ajoutant que :
- on veut considérer \(1\frac{1}{2}\; \times \;6\) comme 1 groupe et demi de 6;
- on veut considérer \(\frac{1}{2}\; \times \;6\) comme 1 demi-groupe de 6.
Ainsi, c’est à la suite d’une interprétation de l’opération que \(\frac{1}{2}\) de 6 est considéré comme une multiplication de \(\frac{1}{2}\) et de 6.
Exemple
Dans une salle de classe de 6e année, \(\frac{1}{2}\) des élèves portent une tuque.
S’il y a 24 élèves dans la salle de classe, combien d’élèves portent une tuque?
- Multiplication effectuée à l’aide du modèle d’ensemble
Pour trouver \(\frac{1}{2}\) de 24, je dispose 24 jetons et j’en trouve la moitié.

La moitié (\(\frac{1}{2}\)) de 24 jetons est 12. Il y a donc 12 élèves qui portent une tuque.
- Multiplication effectuée à l’aide d’une droite numérique
Pour trouver \(\frac{1}{2}\) de 24, je divise 24 par 2, ce qui me donne 12.
Je représente les 24 élèves sous la droite et la moitié de 24 sur le haut de la droite.
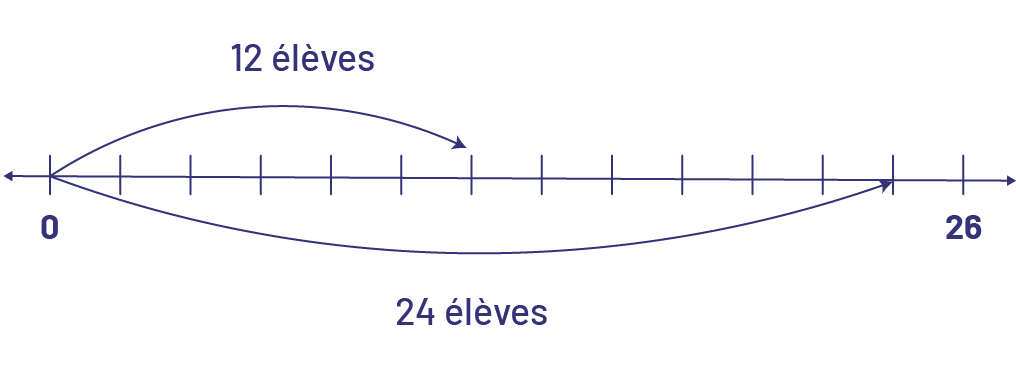
Il y a 12 élèves qui portent une tuque.
À cette année d’études, en s’attardant aux concepts et à une mise en contexte, il est plus pertinent d’approfondir le sens de la fraction d’un ensemble en effectuant un calcul (par exemple, \(\frac{1}{3}\) de 9) que de s’orienter vers la multiplication d’une fraction par un nombre naturel (\(\frac{1}{3}\; \times \;9\)).
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 78-79.
Habileté : diviser un nombre naturel à 1 chiffre par une fraction unitaire, à l’aide d’outils et de schémas
Afin de comprendre une division, il est essentiel d’examiner le sens de la division et la nature des nombres qui la composent. Une division a le sens de partage lorsqu’on cherche la taille des groupes; elle a le sens de groupement lorsqu’on cherche le nombre de groupes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 80.
Ainsi, la division d’un nombre naturel par une fraction (par exemple, \(2\; \div \;\frac{1}{3}\)) se représente bien en utilisant le sens de groupement. Dans ce cas, la fraction est le diviseur.
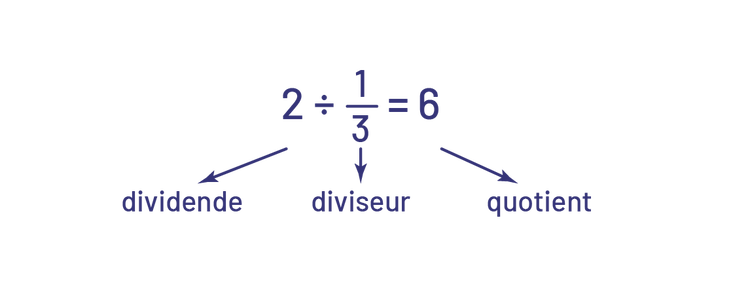
Par exemple, si on a 2 réglisses et que l’on veut remettre à chaque enfant \(\frac{1}{3}\) d’une réglisse, on procède à une division puisqu’il faut séparer une quantité (2 réglisses) en des quantités égales (\(\frac{1}{3}\) de réglisse) pour déterminer le nombre de quantités égales ou de groupes qui peuvent être créés (6 enfants recevront \(\frac{1}{3}\) de réglisse chacun). Dans ce cas, il est important de reconnaître que le quotient exprime un nombre de sections, soit des tiers et non une quantité d’objets (réglisses).
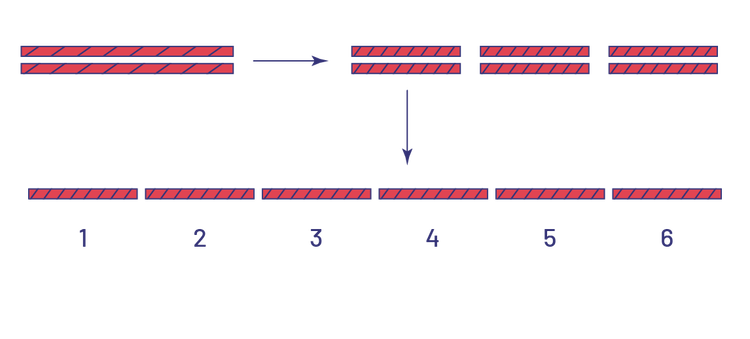
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 81-82.
L’analogie de la soustraction répétée est de mise puisqu’il s’agit de séparer des parties.
Exemple
Dans la division de 2 par \(\frac{1}{4}\) (\(2\; \div \;\frac{1}{4}\)), en faisant \(2\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\;\), on peut créer 8 groupes de \(\frac{1}{4}\). Cependant, le groupe créé est plutôt abstrait puisqu’il s’agit d’un groupe qui est une fraction d’un tout. Les questions « Combien de \(\frac{1}{4}\) peuvent être créés avec 2 touts? » et « Combien de fois \(\frac{1}{4}\) va-t-il dans 2? » peuvent aider à se représenter l’opération.
Exemple
\(4\; \div \;\frac{1}{3}\; = \;12\)
Modèle de surface :
Combien de morceaux de \(\frac{1}{3}\) de tarte peuvent être offerts si on dispose de 4 tartes?
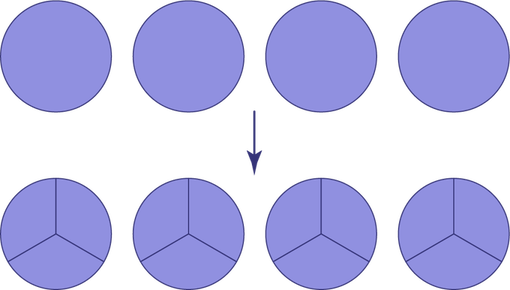
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 100-101.
Modèle de longueur :
La vidéo suivante montre la division d’un nombre naturel par une fraction à l’aide d’un modèle de longueur.
 Description de la vidéo
Description de la vidéo
Description à venir
Connaissance : fraction unitaire
Fraction dont le numérateur est un (1).
Exemples
\(\frac{1}{3}\), \(\frac{1}{9}\)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 35.
