B2.8 Multiply and divide one-digit whole numbers by unit fractions, using appropriate tools and drawings.
Skill: Multiplying One-Digit Whole Numbers by Unit Fractions
In the junior grades, students already have a wealth of knowledge about multiplication. In fact, they have explored concepts related to multiplication using concrete materials, calculators, illustrations and symbols since the primary grades. In Grade 4, multiplying fractions is limited to multiplying a one-digit whole number by a unit fraction. This type of multiplication can be understood by relating it to repeated addition. Thus, students easily grasp that \(3\; \times \;\frac{1}{2}\), which can be read as "3 times one half" is a multiplication which can be represented by repeated addition (that is \(\frac{1}{2}\; + \;\frac{1}{2}\; + \;\frac{1}{2}\)). This should be explored to help students understand the multiplication of fractions.
However, it is more difficult to make sense of multiplying a fraction by a whole number (for example, \(\frac{1}{2}\; \times \;3\)). These situations are explored from the 5th grade onwards. There is a connection between the concept of multiplying by a fraction and that of a fraction of a set. For example, in Grade 2, students learn the meaning of \(\frac{1}{2}\), \(\frac{1}{4}\), and \(\frac{1}{3} \) of a group of up to 10 objects. Later, they consolidate their understanding of the concept of a fraction of a set by applying it to other fractions. In Grade 5, by examining the concept of multiplying a unit fraction by a one-digit whole number, they will learn that the fraction of a set (\(\frac{1}{3}\)of 6 ) is related to multiplication and that this situation can be represented by a multiplication (\(\frac{1}{3}\; \times \;6\)).
Mathematicians were able to make connections to the concept of multiplication of whole numbers by reasoning this way:
- we can consider \(4\; \times \;6\) as 4 groups of 6;
- we can consider \(2\; \times \;8\) as 2 groups of 8.
There is no difficulty in extending this observation to mixed numbers greater than 2:
- we can consider \(4 \frac{1}{2}\; \times \;6\) as 4 and one half groups of 6;
- we can consider \(2\frac{1}{3}\; \times \;12\) as 2 groups and one third of 12.
We generalize this situation (which implies an abstraction, since the group is not "multiplied" as such) by adding that :
- we want to consider \(1\frac{1}{2}\; \times \;6\) as 1 and one half groups of 6;
- we want to consider \(\frac{1}{2}\; \times \;6\) as one half-group of 6.
Thus, through this way of interpretating the operation, \(\frac{1}{2}\) of 6 is considered as a multiplication of \(\frac{1}{2}\) and of 6.
Example
In a Grade 6 classroom, \(\frac{1}{2}\) of the students are wearing toques.
If there are 24 students in the classroom, how many students are wearing toques?
- Multiplication performed using the set model
To determine \(\frac{1}{2}\) of 24, I lay out 24 counters and take half of them.
Half (\(\frac{1}{2}\)) of 24 tokens is 12. There are therefore 12 students wearing a toque.
- Multiplication performed using a number line
To determine \(\frac{1}{2}\) of 24, I divide 24 by 2, which gives me 12.
I represent the 24 students below the line and half of 24 above the line.
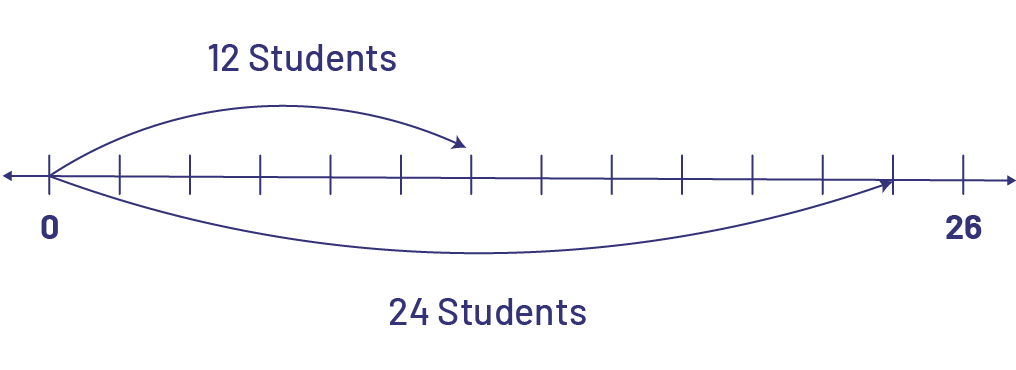
There are 12 students wearing toques.
In this grade, by focusing on concepts and context, it is more relevant to deepen the meaning of the fraction of a whole when performing a calculation (for example, \(\frac{1 }{3}\) of 9) than to focus on the multiplication of a fraction by a whole number (\(\frac{1}{3}\; \times \;9\)).
Source: adapted from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 78-79.
Skill: Dividing a One-Digit Whole Number by a Unit Fraction, Using Tools and Drawings
In order to understand a division, it is essential to examine the meaning of division and the nature of the numbers are used. Division has the meaning of sharing when we look for the size of the groups; it has the meaning of grouping when we look for the number of groups.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 80.
Thus, dividing a whole number by a fraction (for example, \(2\; \div \;\frac{1}{3}\)) is well represented using grouping. In this case, the fraction is the divisor.
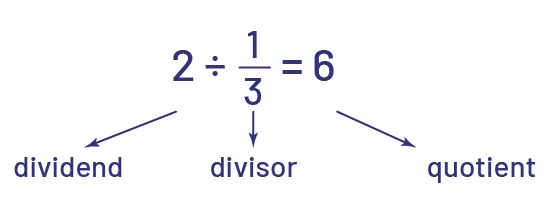
For example, if we have 2 licorice chews and we want to give \(\frac{1}{3}\) of the licorice to each child, we are doing a division since we need to separate one quantity (2 licorice chews) into equal quantities (\(\frac{1}{3}\) of the licorice) to determine the number of equal quantities or groups that can be created (6 children will receive \(\frac{1}{3}\) of the licorice each). In this case, it is important to recognize that the quotient expresses a number of sections, namely, thirds, not a quantity of objects (licorice chews).
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 81-82.
The analogy of repeated subtraction is appropriate since it involves separating out parts.
Example
In dividing by 2 \(\frac{1}{4}\) (\(2\; \div \;\frac{1}{4}\)), doing \(2\; - \; \frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\ ;\), we can create 8 groups of \(\frac{1}{4}\). However, the group created may be rather abstract since it is a group that is a fraction of a whole. The questions "How many \(\frac{1}{4}\) can be created with 2 wholes?" and "How many times does \(\frac{1}{4}\) go in 2?" can help visualize the operation.
Example
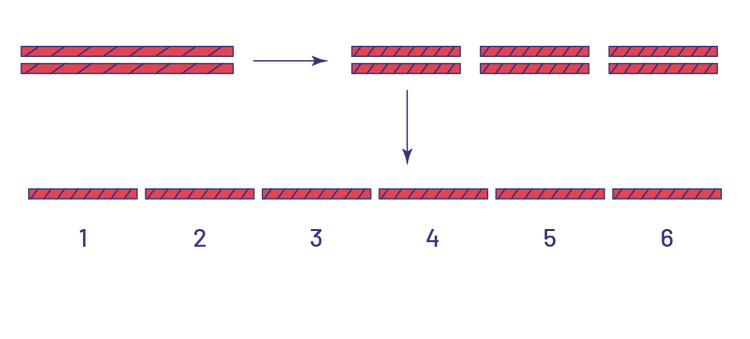
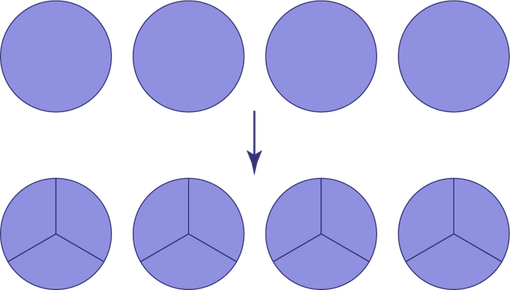
\(4\; \div \;\frac{1}{3}\; = \;12\)
Area Model
How many pieces of pie can be offered if there are 4 pies?
Linear Model
Mathieu wraps gifts in small boxes. He needs 3 feet of ribbon to create 1 decorative bow. If there are 4 yards of ribbon, how many bows can he create?
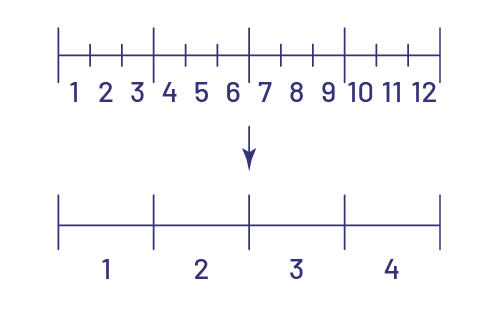
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 100-101.
Knowledge: Unit Fractions
Any fraction that has a numerator of 1.
Examples
\(\frac{1}{3}\), \(\frac{1}{9}\)
Source: The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Educaiton, 2020.