B1.1 Lire et représenter les nombres naturels de 0 jusqu’à un million, à l’aide d’outils et de stratégies appropriés, et décrire de quelles façons ils sont utilisés dans la vie quotidienne.
Activité 1 : au voleur!
Cette activité aide les élèves à développer le sens des grands nombres (par exemple, un million) et à interpréter de façon critique les nombres donnés dans les médias. Le personnel enseignant projette l’article suivant au tableau interactif (ou en remet une copie à chaque élève).
L’article se lit comme suit : « Un cambriolage a eu lieu hier soir à la
banque
de la ville. Selon des sources sûres, 21 liasses de 100 000 dollars chacune ont disparu du coffre-fort principal. Les
policiers sont à la recherche de tout indice pouvant mener à l’arrestation du ou des coupables. Tout renseignement
peut être communiqué au 555-555-5555. »
Après la lecture, le personnel enseignant invite les élèves à échanger entre eux sur la portée de ce vol en posant des questions telles que : « Quel montant d’argent a été volé? Comment écrit-on ce montant en chiffres? » Afin de se faire une idée juste du sens de la quantité volée, le personnel enseignant leur demande combien il faudrait de liasses de 10 000 $ pour obtenir une somme équivalente à la somme volée. Combien de liasses de 1 000 $?
Ces questions font ressortir les relations entre les valeurs de position (par exemple, 1 million c’est aussi 100 dizaines de mille ou 1 000 milliers). L’utilisation d’un tapis de valeur de position ou de billets en papier peut aider les élèves à mieux voir ces relations et déterminer qu’il s’agit d’une escroquerie de plus de 2 millions de dollars.
Le personnel enseignant peut aussi aider les élèves à développer un sens de la quantité volée en posant des questions telles que : « Le montant de 2 100 000 $ représente combien de dollars par habitant de notre ville? Pour une personne qui travaille 8 heures par jour, 250 jours par année au tarif de 15 $ l’heure, combien d’années de travail ce vol représente-t-il? »
Ensuite, demander aux élèves de trouver d’autres exemples d’utilisation de grands nombres dans les journaux, les revues, sites Internet (par exemple, population d’une ville ou d’un pays, montant du budget provincial ou fédéral, coût moyen des maisons) et échanger avec eux sur le sens de ces nombres.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 146-148.
Activité 2 : mon âge? – j’ai 5 650 000 secondes, et toi?
Cette activité permet aux élèves d’examiner de grands nombres et d’évaluer l’importance du choix de l’unité de mesure.
Lorsque les adultes rencontrent des enfants, il est fréquent de leur demander leur âge. Généralement, l’âge est calculé en années, mais les jeunes enfants répondent souvent : « J’ai 5 ans et 6 mois » tout comme une maman dira de son bébé qu’il a « 18 mois ». Pourquoi, en effet, ne pas calculer l’âge en utilisant d’autres unités de mesure que l’année (par exemple, seconde, minute, heure, jour, semaine, mois)?
Proposer aux élèves de calculer leur âge en fonction de diverses unités de mesure. Pour y arriver, les élèves doivent d’abord connaître les liens entre les mesures de temps (par exemple, il y a 60 secondes dans 1 minute, 60 minutes dans 1 heure, 24 heures dans 1 journée, 7 jours dans 1 semaine; il y a 12 mois, 52 semaines ou 365 jours dans 1 année). Un élève de 10 ans pourra donc affirmer d’être âgé de plus de 3 650 jours ou encore de plus de 520 semaines ou 120 mois. L’élève pourra même ajouter qu’il a vécu plus de 87 600 heures ou plus de 5 256 000 minutes ou même plus de 300 millions de secondes.
Après que les élèves ont fait des calculs mentalement, sur papier ou à l’aide d’une calculatrice, discuter avec eux du choix des stratégies de calcul et des unités de mesure employées. Souligner l’importance d’arrondir les nombres compte tenu du fait qu’il n’est pas nécessaire d’obtenir une réponse avec un haut niveau d’exactitude. Par exemple, après avoir calculé qu’une année équivaut à 525 600 minutes, un ou une élève peut choisir d’arrondir ce nombre à un demi-million de minutes. Un ou une autre élève peut choisir d’arrondir le nombre de semaines dans une année à 50 pour faciliter ses calculs et ensuite, faire ou non l’ajout des semaines manquantes à la fin. À l’inverse, certains élèves peuvent chercher une réponse plus précise en tenant compte, par exemple, de la date exacte de naissance ou des années bissextiles.
Discuter avec les élèves des avantages de mesurer l’âge en années. En effet, les âges donnés en secondes sont très grands, plus difficiles à manipuler, à lire, à exprimer ou à écrire, et leur sens, plus difficile à saisir. Par exemple, le fait que la différence d’âge entre deux élèves de la même classe soit de un demi-million de minutes peut sembler énorme alors qu’en réalité, cela représente moins de un an de différence. Dans ce cas, il serait plus pertinent d’examiner la différence d’âge en mois.
Discuter aussi de l’avantage, dans certains cas, d’utiliser une unité de mesure autre que les années. En effet, dans le cas de jeunes enfants, il est courant de donner l’âge en mois (par exemple, bébé de 16 mois). Parfois, le choix de l’unité de mesure fait partie d’une stratégie de marketing (par exemple, une garantie prolongée de 36 mois peut sembler plus avantageuse qu’une garantie de 3 ans).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 148-149.
Activité 3 : et ensuite?
Cette activité intègre des concepts en Nombres ainsi qu’en Sens de l’espace. Elle permet d’abord aux élèves de se construire une représentation mentale de grands nombres jusqu’à 1 million et ensuite de faire le lien avec le concept d’aire mesurée en centimètres et en mètres carrés.
Matériel
- 1 petit carré unitaire (\(1\;{\rm{cm}}\; \times \;1\;{\rm{cm}}\))
- 10 bandes de papier (\(10\;\;\;{\rm{cm}}\; \times \;1\;{\rm{cm}}\)), chacune comptant 10 carrés unitaires
- photocopies d’un grand carré (\(10\;\;\;{\rm{cm}}\; \times \;10\;\;\;{\rm{cm}}\)) comptant 100 carrés unitaires (2 par élève)
- grandes feuilles de papier ou papier journal
- colle ou ruban adhésif
Dans la première partie de l’activité, les élèves développent progressivement un sens de la quantité représentée par de grands nombres (1 000, 10 000, 100 000, 1 000 000).
Montrer aux élèves le petit carré (Figure 1) et leur indiquer qu’il représente 1 carré unitaire. Montrer ensuite une bande qui équivaut à 10 carrés unitaires (Figure 2) et leur demander comment faire pour représenter 100 carrés unitaires. À partir de leur sens du nombre et de leurs expériences antérieures avec le matériel de base dix, les élèves devraient répondre qu’ils ou elles peuvent assembler 10 bandes l’une à côté de l’autre de façon à former un grand carré de 10 cm sur 10 cm (Figure 3). Il est important de faire ressortir que les 10 bandes constituent 10 dizaines de carrés unitaires ou 100 carrés unitaires.
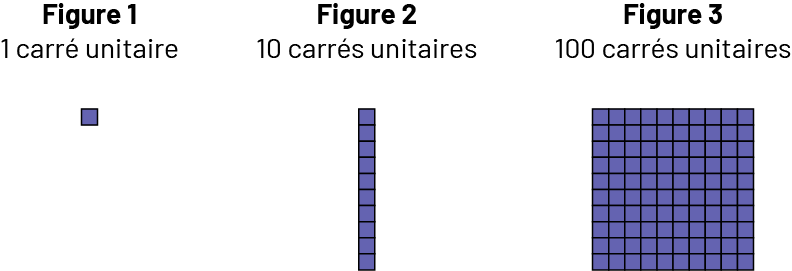La figure un, la figure deux et la figure trois sont alignées côte à côte.
La
figure un est représentée par un carré unitaire. La figure deux est représentée par une tour de dix carrés
unitaires.
Et la figure trois est une grille dix par dix qui équivaut à cent carrés unitaires.
Remettre à chaque élève deux copies de la figure 3 (100 carrés unitaires). Grouper les élèves par cinq et leur demander de représenter 1 000 carrés unitaires. Ils ou elles pourraient les disposer de façon à former une grande bande mesurant 10 cm sur 100 cm (Photo A) à partir de leurs 10 copies de 100 carrés unitaires.
Remettre ensuite à chaque groupe une grande feuille de papier ou du papier journal et leur demander de représenter 10 000 carrés unitaires. Pour ce faire, les élèves peuvent prendre leur bande de 1 000 carrés unitaires et la reproduire 10 fois sur la grande feuille ou sur le papier journal (Photo B) de façon à former un carré de 100 cm sur 100 cm.
Demander maintenant à tous les élèves de la classe de se regrouper pour représenter 100 000 carrés unitaires. Ils peuvent par exemple assembler 10 représentations de 10 000 carrés unitaires (Photo C) de façon à former une bande de 100 cm sur 1 000 cm. Prévoir un espace assez grand (par exemple, corridor) puisque la bande mesurera 10 m de long.
Pour représenter 1 000 000 de carrés unitaires, il faut se rendre à l’extérieur ou au gymnase et assembler 10 grandes bandes de 100 000 carrés unitaires, ou délimiter l’espace qu’occuperaient ces 10 bandes, de façon à former un carré de 1 000 cm sur 1 000 cm (Photo D).
Tout au long de l’activité, attirer l’attention sur la relation multiplicative par 10 qui définit chaque passage d’une étape à l’autre, ainsi que sur la suite de représentations composée d’un carré, d’une bande, d’un plus grand carré, d’une plus grande bande… Par exemple, on multiplie un carré unitaire par 10 pour obtenir une bande formée de 10 carrés unitaires, on multiplie la bande par 10 pour obtenir un plus grand carré formé de 100 carrés unitaires… (Figure 4 et Photo E). Cette régularité est identique à celle que l’on retrouve dans les valeurs de position de notre système de numération (unités, dizaines, centaines…). Au cours d’un échange mathématique, il est important de faire ressortir les liens entre les nombres pour que le concept de quantité soit bien compris. Par exemple, 1 000 unités sont égales à 100 dizaines d’unités ou à 10 centaines d’unités.
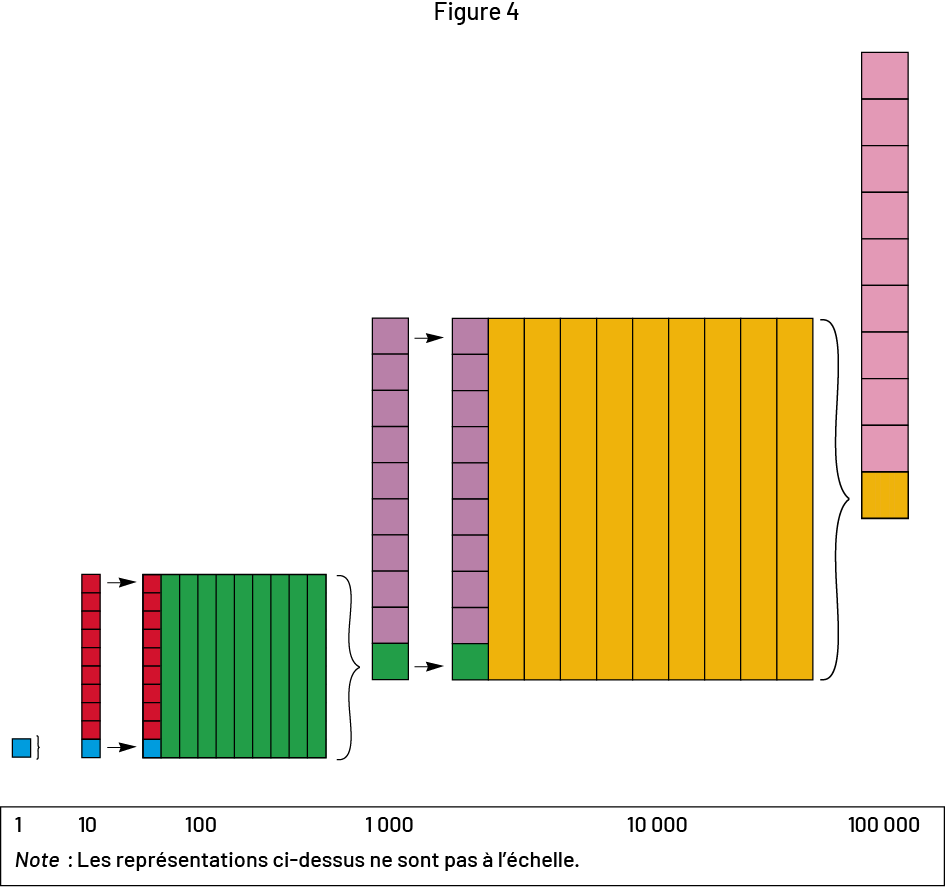La figure quatre est illustrée à partir de réglettes. La description se
fait de
gauche à droite. Un carré bleu représente un. Ensuite, une tour d’unités faite d’un carré bleu et de neuf carrés
rouges représente dix. Cette tour est ensuite dupliquée et assemblée avec neuf réglettes vertes qui font la même
hauteur. La réglette verte représente donc cent. Une accolade mène au prochain assemblage. Une unité verte forme
une
tour avec neuf unités pourpres, ce qui représente mille. Cette tour est ensuite dupliquée et assemblée avec neuf
réglettes jaunes de la même hauteur, ce qui représente dix mille. Une accolade mène au dernier assemblage. Une
unité
jaune forme une tour avec neuf unités roses, ce qui correspond à cent mille. « Note : Les représentations
ci-dessus ne
sont pas à l’échelle. »
Dans la deuxième partie de l’activité, amener les élèves à établir des liens entre la suite de représentations de grands nombres et le concept d’aire. Leur indiquer que le carré unitaire mesure 1 cm sur 1 cm et leur demander d’en déterminer l’aire (1 cm2). Leur demander ensuite de déterminer l’aire de la bande formée de 10 carrés unitaires (10 cm2), puis de chacune des autres représentations produites dans la première partie de l’activité.
Il importe aussi de faire des liens entre les unités de mesure carrées. Par exemple, l’aire du carré formé de 10 000 carrés unitaires est 10 000 cm2 (100 cm sur 100 cm) ou 1 m2 (1 m sur 1 m). Par la suite, les élèves peuvent utiliser les bandes et les carrés fabriqués pour estimer et mesurer l’aire de diverses surfaces planes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 149-153.