B1.1 Read and represent whole numbers up to and including one million, using appropriate tools and strategies, and describe various ways they are used in everyday life.
Activity 1: Thief!
This activity helps students develop an understanding of large numbers (such as one million) and supports them to critically interpret numbers in the media. Project the following article on the interactive whiteboard (or give a copy to each student).

After reading, invite students to share with each other the significance of this theft by asking questions such as, "How much money was stolen? How do you write that amount in numbers?" In order to get a fair idea of the meaning of the amount stolen, teachers ask them how many bundles of $10 000 it would take to equal the amount stolen. How many bundles of $1000?
These questions highlight the relationships between place values (for example, 1 million is also 100 tens of thousands or 1000 thousands). Using a place value mat or paper bills can help students better see these relationships and determine that this is a scam for over $2 million.
Teachers can also help students develop a sense of the amount stolen by asking questions such as, "The $2 100 000 is how many dollars per person in our city? For a person who works 8 hours a day, 250 days a year at $15 an hour, how many years of work does this theft represent?
Next, ask students to find other examples of the use of large numbers in newspapers, magazines, or websites (population of a city or country, amount of the provincial or federal budget, average cost of homes) and discuss with them what these numbers mean.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 146-148.
Activity 2: My Age? - I am 5 650 000 Seconds Old, How Old Are You?
This activity allows students to examine large numbers and assess the importance of the choice of unit of measurement.
When adults meet children, it is common to ask their age. Generally, age is calculated in years, but young children often say, "I am 5 years and 6 months old," just as a mother will say of her baby that he is "18 months old". Why not calculate age using units of measurement other than years (seconds, minutes, hours, days, weeks, months)?
Have students calculate their age in terms of various units of measurement. To do this, students must first be aware of the relationship between time measurements (there are 60 seconds in 1 minute, 60 minutes in 1 hour, 24 hours in 1 day, 7 days in 1 week; there are 12 months, 52 weeks or 365 days in 1 year). A 10 year old student could therefore claim to be more than 3650 days old or more than 520 weeks or 120 months old. The student could even add that he or she has lived more than 87 600 hours or more than 5 256 000 minutes or even more than 300 million seconds.
After students have completed calculations mentally, on paper, or with a calculator, discuss with them the choice of calculation strategies and units of measurement used. Emphasize the importance of rounding numbers, as it is not necessary to obtain an answer with a high degree of accuracy. For example, after calculating that one year is 525 600 minutes, a student may choose to round this number to half a million minutes. Another student may choose to round the number of weeks in a year to 50 to make the calculation easier and then add or not add the missing weeks at the end. Alternatively, some students may seek a more accurate answer by taking into account, for example, the exact date of birth or leap years.
Discuss with students the advantages of measuring age in years. Ages given in seconds are very large, more difficult to manipulate, read, express or write, and more difficult to grasp in meaning. For example, the fact that the difference in age between two students in the same class is half a million minutes may seem enormous when in reality it represents less than a year's difference. In this case, it would be more relevant to examine the age difference in months.
Also discuss the advantage, in some cases, of using a unit of measurement other than years. For example, in the case of young children, it is common to give the age in months (for example, 16-month-old baby). Sometimes the choice of unit of measurement is part of a marketing strategy (for example, a 36-month extended warranty may seem more advantageous than a 3-year warranty).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels,p 148-149.
Activity 3: What Next?
This activity integrates concepts in Number and Spatial Sense. First, it enables students to construct a mental representation of large numbers up to 1 million, and then to make the link with area measured in centimetres and square metres.
Materials
- 1 square unit (1cm x 1 cm)
- 10 paper strips (10 cm x 1 cm), with 10 square units each
- photocopies of a large square (10 cm x 10 cm) with 100 square units (2 per student)
- large sheets of paper or newspaper
- glue or tape
In the first part of the activity, students gradually develop a sense of quantity represented by large numbers (1000, 10 000, 100 000, 1 000 000).
Show students the small square (Figure 1) and tell them that it represents 1 square unit. Then show a strip that equals 10 square units (Figure 2) and ask them how to represent 100 square units. Using their number sense and previous experiences with base ten blocks, students should respond that they can put 10 strips together to form a large 10 cm by 10 cm square (Figure 3). It is important to emphasize that the 10 strips constitute 10 tens square units or 100 square units.

Give each student two copies of Figure 3 (100 square units). Group the students into groups of five and ask them to represent 1000 square units. They could arrange them to form a large strip measuring 10 cm by 100 cm (Photo A) from their 10 copies of 100 square units.

Then give each group a large sheet of paper or newsprint and ask them to represent 10 000 square units. To do this, students can take their strip of 1000 square units and reproduce it 10 times on the large sheet of paper or newsprint (Photo B) to form a 100 cm by 100 cm square.

Now ask all students in the class to come together to represent 100 000 square units. For example, they could assemble 10 representations of 10 000 square units (Photo C) to form a 100 cm by 1000 cm strip. Provide a large enough space (for example., hallway) since the strip will be 10 m long.

To represent 1 000 000 square units, go outside or to the gym and assemble 10 large strips of 100 000 square units, or mark out the space that these 10 strips would occupy, to form a 1000 cm by 1000 cm square (Photo D).

Throughout the activity, draw attention to the multiplicative relationship by 10 that defines each move from one step to the next, as well as the fact that each representation in the sequence is composed of a square. For example, a square unit is multiplied by 10 to obtain 10 square units, and that is multiplied by 10 to obtain a larger square formed of 100 square units…(Figure 4 below and Photo E). This pattern is identical to that found in the place values of our base ten number system (ones, tens, hundreds…). During a mathematical discussion, it is important to point out the connections between numbers so that the concept of quantity is understood. For example, 1000 units equals 100 tens or 10 hundreds.
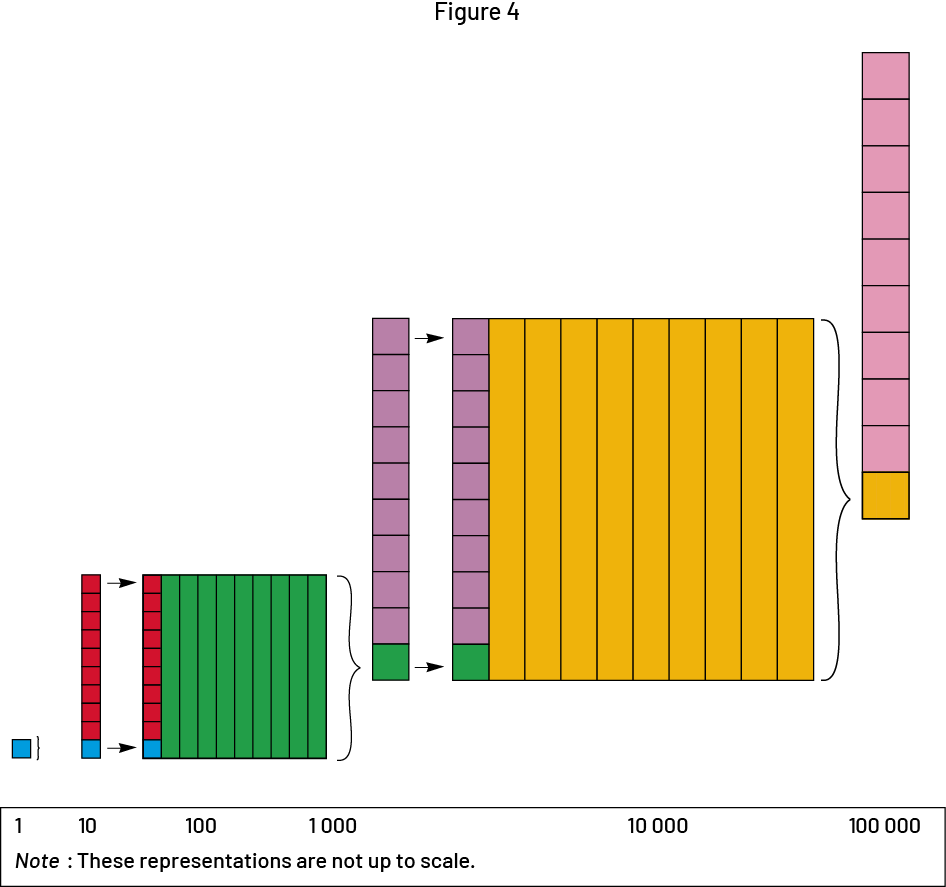

In the second part of the activity, have students make connections between the sequence of large number representations and the concept of area. Tell them that the square unit measures 1 cm by 1 cm and ask them to determine its area (1 cm2). Then ask them to determine the area of the strip of 10 square units (10 cm2) and then each of the other representations produced in the first part of the activity.
It is also important to make connections between the square units of measurement. For example, the area of the square made up of 10 000 square units is 10 000 cm2 (100 cm by 100 cm) or 1 m2 (1 m by 1 m). Later, students can use the strips and squares made to estimate and measure the area of various flat surfaces.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 149-153.
