B2.12 Résoudre des problèmes comprenant des rapports, y compris des pourcentages et des taux, à l’aide d’outils et de stratégies appropriés.
Activité 1 : problèmes de proportionnalité
Voici deux exemples de problèmes de proportionnalité qui peuvent être résolus à l’aide des modèles expliqués dans la section Habiletés et connaissances :
Exemple 1
Les cahiers distribués dans les écoles sont vendus en paquets de 12 cahiers.
a) Combien de cahiers y a-t-il dans 13 paquets? (156 cahiers)
b) Si l’école a besoin de 180 cahiers, combien de paquets doit-elle commander? (15 paquets)
Exemple 2
Les yogourts se vendent soit à l’unité, soit au prix de 4 $ pour 12 yogourts.
a) Combien coûteront 72 yogourts? 21 yogourts? (24 $, 7 $)
b) Combien de yogourts peut-on acheter avec 10 $? 16 $? (30 yogourts, 48 yogourts)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 54.
Poser des questions aux élèves telles que :
- Dans ces mises en situation, s’agit-il d’une comparaison relative ou absolue? Comment le sais-tu?
- Comment pourrait-on écrire les rapports de façon symbolique? Justifie ta réponse.
- Selon toi, quelles stratégies peut-on utiliser pour résoudre les problèmes? Pourquoi?
- Un tableau de rapports serait-il utile pour résoudre ces mises en situation? Comment le sais-tu?
- Quels sont les coefficients de proportionnalité? À quoi servent-ils?
Demander aux élèves de trouver des rapports équivalents. Comparer les résultats des élèves.
Activité 2 : rapports de fruits
Présenter cette mise en situation aux élèves.
Les élèves peuvent créer et représenter un rapport à partir d’un ensemble de fruits. S’il y a 15 fruits (10 poires et 5 bananes), ils peuvent faire des rapports tels que :
- 10 poires pour 5 bananes ou 10 : 5 ou \(\frac{{10}}{5}\)
- 5 bananes pour 15 fruits ou 5 : 15 ou \(\frac{5}{{15}}\)
- 10 poires pour 15 fruits ou 10 : 15 ou \(\frac{{10}}{{15}}\)
Les élèves en 5e année apprennent aussi la notion de rapports ou taux équivalents. Dans l’exemple des fruits ci-dessus, on peut représenter les rapports mentionnés ci-haut par des rapports équivalents. Cette notion de rapports équivalents développe le raisonnement proportionnel.
- 10 poires pour 5 bananes ou 10 : 5 ou \(\frac{{10}}{5}\) ou 2
puisqu’on peut dire que pour chaque ensemble de 2 poires il y a une banane.
Image L’illustration montre cinq rangées de deux poires et une colonne de cinq bananes placée vis-à-vis. Les deux premières poires sont regroupées ensemble et sont aussi regroupées avec la première banane en indiquant : deux sur un ou deux divisé par un ou deux poires pour une banane. Sous les fruits, il est écrit dix divisé par cinq.
- 5 bananes pour 15 fruits ou 5 : 15 ou \(\frac{5}{{15}}\) ou \(\frac{1}{3}\)
puisqu’on peut dire qu’il y a une banane pour chaque ensemble de 3 fruits. On peut également dire qu’environ 33 % des fruits sont des bananes.
Image L’illustration montre une colonne de cinq bananes, chacune accompagnée de deux poires. La première banane est encadrée et elle est aussi regroupée avec les deux poires à côté d’elle. Il est écrit : un tiers ou un divisé par trois ou une banane pour trois fruits. Sous les fruits, il est écrit cinq deux-points 15.
- 10 poires pour 15 fruits ou 10:15 ou \(\frac{{10}}{{15}}\) ou \(\frac{2}{3}\)
puisqu’on peut dire qu’il y a 2 poires pour chaque ensemble de 3 fruits. On peut également dire qu’environ 67 % des fruits sont des poires.
Image L’illustration montre cinq rangées de deux poires et une colonne de cinq bananes placée vis-à-vis. Les deux premières poires sont regroupées ensemble et sont aussi regroupées avec la première banane en indiquant : deux tiers ou deux divisé par trois ou deux poires pour trois fruits. Sous les fruits, il est écrit : dix deux-points 15.
Nous pouvons représenter des rapports bananes et poires à l’aide d’un tableau de rapports.
Dans ce tableau, on peut également reconnaître qu’il existe une relation de proportionnalité entre le nombre de bananes et le nombre de poires, soit \( \times \;2\). Le coefficient de proportionnalité est de 2. On multiplie le nombre de bananes par 2 pour obtenir le nombre de poires.
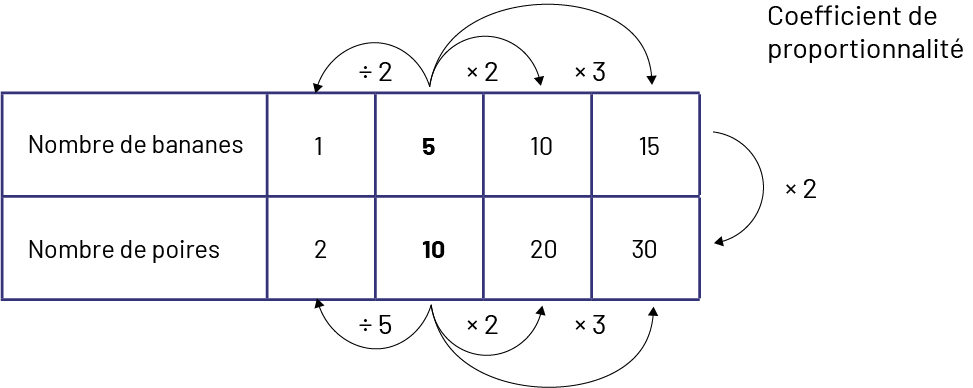Image Un tableau possède deux rangées de cinq cases. Première rangée : Nombre de bananes, un, cinq, dix, 15. Une flèche relie cinq à un en indiquant divisé par deux. Une flèche relie cinq à dix en indiquant fois deux. Et une flèche relie cinq à 15 en indiquant fois trois. Deuxième rangée : Nombre de poires, deux, dix, 20, 30. Une flèche relie dix à deux en indiquant divisé par cinq. Une flèche relie dix à 20 en indiquant fois deux. Une flèche relie dix à 30 en indiquant fois trois. Et une flèche relie le 15 de la rangée du haut et le 30 de la rangée du bas en indiquant fois deux. À côté du tableau, il est écrit : Coefficient de proportionnalité.
On peut donc dire que les rapports équivalents sont :
\(\frac{1}{2}\; = \;\frac{5}{{10}}\; = \;\frac{{10}}{{20}}\; = \;\frac{{15}}{{30}}\) ou 1 : 2 = 5 : 10 = 5 : 10 = 15 : 30
Activité 3 : résoudre des situations de taux et de rapports
Présenter des contextes semblables à ceux-ci afin d’explorer et de faire résoudre des situations de rapports et de taux.
- Luca lit 34 pages en 2 heures. À ce rythme, combien de pages aura-t-il lues en 5 heures? S’il y a 100 pages dans son livre, quel pourcentage du livre aura-t-il lu?
- À une école, 4 élèves sur 5 jouent à des sports à la récréation. Combien d’élèves de la classe de Mme Claro cela pourrait-il représenter si elle a 30 élèves? Quel pourcentage des élèves de la classe jouent à des sports à la récréation?
Activité 4 : jeu d’association
Demander aux élèves de créer des cartes représentant des taux et rapports équivalents avec des images. Préparer des cartes avec le taux ou le rapport écrit symboliquement. Par exemple, 2 : 10, 1 : 5, 5 $/15, etc.
Distribuer une carte aux élèves et leur demander de circuler pour trouver la carte qui représente le même taux ou rapport. À noter que ce jeu pourrait aussi être placé dans un centre d’apprentissage.
Faire un retour avec les élèves après l’activité. Leur poser des questions telles que :
- Comment avez-vous trouvé l’activité? Comment est-ce que vous vous sentiez durant l’activité? Qu’est-ce qui représentait un défi pour vous?
- Quels rapports équivalents avez-vous trouvés? Comment peut-on savoir qu’il s’agit d’un rapport équivalent? Explique ton raisonnement.
- Quelles stratégies peut-on utiliser pour trouver les rapports équivalents? Comment le sais-tu?