B2.12 Solve problems involving ratios, including percents and rates, using appropriate tools and strategies.
Activity 1: Proportionality Problems
Here are two examples of proportionality problems that can be solved using the models explained in the Skills and Knowledge section:
Example 1
The notebooks distributed in schools are sold in packs of 12 notebooks.
a) How many notebooks are there in 13 packs?(156 notebooks)
b) If the school needs 180 notebooks, how many packs should it order?(15 packs)
Example 2:
Yogurts are sold either individually or for $4 for 12 yogurts.
a) How much will 72 yogurts cost? 21 yogurts ($24, $7)
b) How many yogurts can you buy with $10? $16?(30 yogurts, 48 yogurts)
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 54.
Ask students questions such as:
- In these situations, is it a relative or absolute comparison? How do you know?
- How could the rates be written symbolically? Justify your answer.
- What strategies do you think can be used to solve the problems? Explain your thinking.
- Would a ratio table be helpful in solving these scenarios? How do you know?
- What are the coefficients of proportionality? What are they used for?
Ask students to find equivalent ratios. Compare students' results.
Activity 2: Fruit Ratios
Present this situation to the students.
Students can create and represent a ratio from a set of fruits. If there are 15 fruits (10 pears and 5 bananas), they can make ratios such as:
- 10 pears for 5 bananas or \(10\;:\;5\) or \(\frac{10}{5}\)
- 5 bananas for 15 fruits or \(5\;:\;15\) or \(\frac{5}{{15}}\)
- 10 pears for 15 fruits or \(10\;:\;15\) or \(\frac{{10}}{{15}}\)
- 10 pears for 5 bananas or \(10\;:\;5\;{\rm{or}}\;\frac{10}{5}\)
- 5 bananas for 15 fruits or \(5\;:\;15\;{\rm{or}}\;\frac{5}{{15}}\)
- 10 pears for 15 fruits or 10:15 or \(\frac{10}{15}\) or \(\frac{2}{3}\)
- Luca reads 34 pages in 2 hours. At this rate, how many pages will he have read in 5 hours? If there are 100 pages in his book, what percentage of the book will he have read?
- At one school, 4 out of 5 students play sports at recess. How many students in Ms. Claro's class would this represent if she had 30 students? What percentage of students in the class play sports at recess?
- How did you find the activity? How did you feel during the activity? What was challenging for you?
- What equivalent ratios did you find? How do you know that they are equivalent ratios? Explain your reasoning.
- What strategies can be used to find the equivalent ratios? How do you know?

We can say that for each set of 2 pears there is one banana.
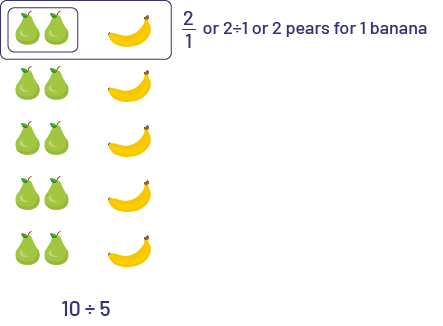
We can say that there is one banana for every three fruits. We can also say that about 33% of the fruits are bananas.

We can say that there are 2 pears for every 3 fruits. We can also say that about 67% of the fruits are pears.

We can represent the banana and pear ratios using a ratio table.
In this table, we can also recognize that there is a proportional relationship between the number of bananas and the number of pears, that is, \(\times \;2\). The proportionality coefficient is 2. We multiply the number of bananas by 2 to get the number of pears.
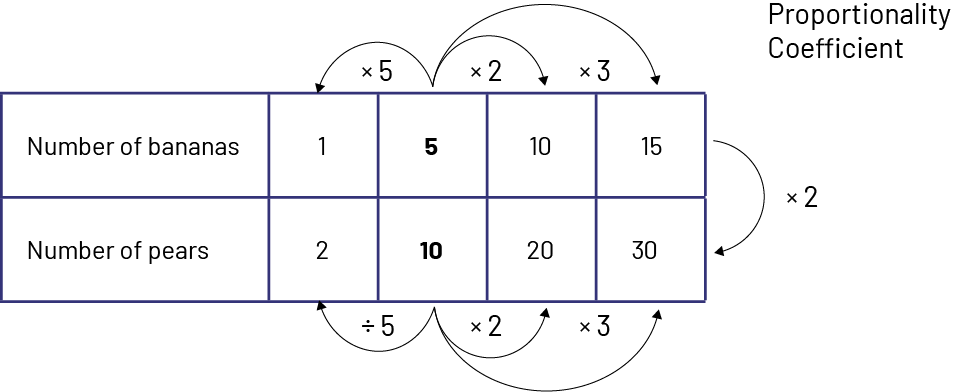
So we can say that the equivalent ratios are:
\(\frac{1}{2}\; = \;\frac{5}{10}\; = \;\frac{10}{20}\; = \;\frac{15}{30}\) or 1:2 = 5:10 = 10:20 = 15:30
Activity 3: Resolving Rate and Ratio Situations
Present contexts similar to these in order to explore ratio and rate situations and have students resolve them.
Activity 4: Matching Game
Have students create cards representing equivalent rates and ratios with pictures. Prepare cards with the rate or ratio written symbolically. For example, 2:10, 1:5, $5/15, etc.
Distribute a card to students and have them circulate to find the card that represents the same rate or ratio. Note that this game could also be placed in a learning centre.
Debrief with students after the activity. Ask them questions such as:
