B2.6 Représenter des nombres composés sous la forme d’une multiplication de ses facteurs premiers, y compris à l’aide de l’arbre de facteurs.
Activité 1 : aires de rectangles
L’habileté à reconnaître qu’un nombre est premier ou composé peut faciliter la résolution de problèmes.
Exemple
Les élèves doivent créer un rectangle dont les dimensions sont des valeurs entières.
Quelles sont les dimensions possibles du rectangle si son aire doit mesurer 24 cm2? 36 cm2? 23 cm2? 11 cm2? 54 cm2?
En reconnaissant que 23 et 11 sont des nombres premiers, les élèves peuvent justifier que dans chacun de ces deux cas, il n’existe qu’un seul ensemble de dimensions possibles (soit un rectangle de 1 cm sur 23 cm et un rectangle de 1 cm sur 11 cm). Afin de déterminer les dimensions possibles des trois autres rectangles, ils doivent examiner les facteurs possibles de 24, de 36 et de 54.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 59.
Activité 2 : différencier les nombres premiers des nombres composés à l’aide de l’arbre des facteurs
Présenter la liste des nombres ci-dessous aux élèves.
- 31
- 26
- 38
- 59
- 67
- 16
- 40
Demander aux élèves d’identifier les nombres premiers ainsi que les nombres composés.
Poser des questions aux élèves telles que :
- S’agit-il d’un nombre premier ou d’un nombre composé? Comment le sais-tu?
- Lesquels de ces nombres peuvent être composés et décomposés par la multiplication? Pourquoi?
- Quels sont les facteurs premiers des nombres? Explique ton raisonnement.
- Comment peut-on démontrer la décomposition d’un nombre en d’autres facteurs à l’aide de l’arbre de facteurs? Justifie ta réponse.
Activité 3 : représenter les nombres composés à l’aide de rectangles
Présenter l’aire de ces quatre rectangles aux élèves.
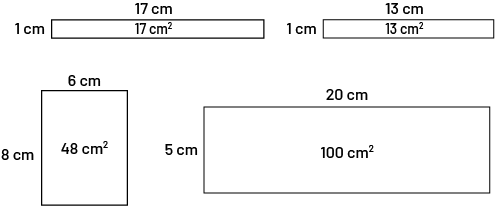Image Quatre rectangles sont présentés. Le premier mesure un centimètre par 17 centimètres pour un total de 17 centimètres carrés. Le deuxième mesure un centimètre par 13 centimètres pour un total de 13 centimètres carrés. Le troisième mesure huit centimètres par six centimètres pour un total de 48 centimètres carrés. Et le quatrième mesure cinq centimètres par vingt centimètres pour un total de cent centimètres carrés.
Demander aux élèves de tenter de construire deux rectangles différents, mais ayant le même aire, pour chacun des rectangles illustrés ci-dessus.
Poser des questions telles que :
- Comment peut-on décomposer le nombre 13? 17? 48? 100? Explique ton raisonnement.
- Comment la multiplication peut-elle aider à composer et décomposer des nombres?
- Comment l’arbre de facteurs montre-t-il les différentes façons dont un nombre peut être décomposé? Justifie ta réponse.
- En comparant les différents rectangles construits, que remarque-t-on?
- Que peut-on constater lorsque l’aire d’un rectangle est un nombre premier? Un nombre composé?