B2.6 represent composite numbers as a product of their prime factors, including through the use of factor trees
Activity 1: Arrays
The ability to recognize that a number is prime or composite can facilitate problem solving.
Example
Students are asked to create a rectangle with dimensions that are integer values.
What are the possible dimensions of the rectangle if its area is 12 cm2? 91 cm2? 17cm2? 54 cm2?
Recognizing that 23 and 11 are prime numbers, students can justify that in each of these two cases there is only one set of possible dimensions (i.e., a rectangle of 1 cm by 23 cm and a rectangle of 1 cm by 11 cm). In order to determine the possible dimensions of the other three rectangles, they must examine the possible factors of 24, 36, and 54.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 59.
Activity 2: Differentiate Prime Numbers from Composite Numbers Using the Factor Tree
Present the list of numbers below to the students.
- 31
- 26
- 38
- 59
- 67
- 16
- 40
Ask students to identify prime numbers as well as composite numbers.
Ask students questions such as:
- Is it a prime number or a composite number? How do you know?
- Which of these numbers can be composed and decomposed by multiplication? Why is that?
- What are the prime factors of numbers? Explain your reasoning.
- How can you demonstrate the decomposition of a number into other factors using the factor tree? Justify your answer.
Activity 3: Represent Composite Numbers Using Arrays
Present the area of these four rectangles to the students.
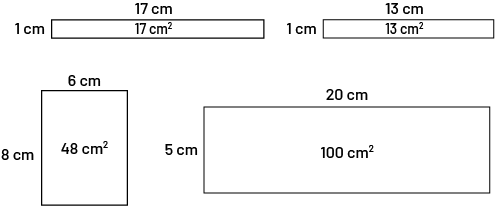
Ask students to construct two different rectangles than those shown above with areas of 13 cm2, 17 cm2, 48 cm2 and 100 cm2.
Ask questions such as:
- How can we decompose the number 13? 17? 48? 100? Explain your reasoning.
- How can multiplication help with composing and decomposing numbers?
- How does the factor tree show the different ways a number can be decomposed? Justify your answer.
- Comparing the different rectangles constructed, what do you notice?
- What can be seen when the area of a rectangle is a prime number? A composite number?