B2.7 Représenter et résoudre des problèmes relatifs à la multiplication d’un nombre naturel à trois chiffres par un nombre décimal jusqu’aux dixièmes, à l’aide d’algorithmes.
Activité 1 : la recette
Partager la mise en situation suivante avec les élèves :
Un rassemblement communautaire a lieu à l’école dans un mois. Il y a 120 invités au gymnase de l’école. Chaque classe a ses responsabilités, et les élèves de notre classe sont responsables de la nourriture. Des plats de charcuterie seront servis.
Fournir une liste d’aliments qui contient sa masse par portion. Expliquer aux élèves que chaque personne mangera environ 3 portions d’aliments. Inviter les élèves à choisir les aliments qui seront mangés par les invités et utiliser une stratégie de leur choix pour calculer la masse totale de chaque aliment.
Exemple
Brie : 30,2 g/tranche
Camembert : 28,4 g/tranche
Dinde fumée : 89,9 g/tranche
Jambon blanc : 85,3 g/tranche
Raisins : 180,3 g/portion
Craquelins : 62,1/portion
Poser des questions aux élèves telles que :
- Quelle quantité de brie devrez-vous commander? De dinde fumée? De jambon blanc? De raisins? De craquelins? Comment le savez-vous?
- Si seulement 110 invités se présentent à l’événement, quelle quantité de chaque aliment devrez-vous préparer? Justifie ta réponse.
- Si le fournisseur n’a malheureusement pas de dinde fumée en stock, qu’est-ce que vous pourriez faire pour remédier à la situation? Quelle quantité de chaque aliment devrez-vous commander? Explique ton choix.
- Quel algorithme peut-on utiliser pour résoudre le problème? Pourquoi?
- En comparant les différents algorithmes utilisés, que remarque-t-on?
- Comment peut-on s’assurer que nos calculs soient vraisemblables? Justifie ta réponse.
Activité 2 : j’estime le résultat des multiplications
Présenter les séries d’opérations apparentées aux élèves. Inviter ensuite les élèves à remplir les cases de la colonne Estimation des prochains tableaux et à déterminer le produit. Discuter des stratégies utilisées.
Exemple

Image Un tableau possède trois colonnes : Opération, Estimation, Produit.Dans la colonne opération il est écrit : « cinq fois 25 », avec une flèche pointant à droite, et « cinq fois deux virgule cinq », avec une flèche pointant à droite.Dans la colonne Estimation, vis-à-vis la première flèche, il est écrit : « cinq groupes de 25, donc 125 »; et vis-à-vis la deuxième flèche, il est écrit : « cinq groupes de deux, soit environ dix ».Dans la colonne estimation, il est écrit, entre parenthèses : « puisque les chiffres un, deux et cinq se retrouvent dans cet ordre dans le produit. » En dessous, il y a une flèche pointant à droite vers le nombre 125. Sous ceci, il y a une flèche pointant à droite vers le nombre douze virgule cinq.

Image Deux tableaux possèdent trois colonnes : Opération, Estimation, Produit. Premier tableau. Dans la colonne Opérations, il y a trois cases contenant respectivement les multiplications suivantes : quatre virgule six fois deux, quatre virgule six fois vingt et quatre virgule six fois 200. La colonne Estimation est complètement vide. Et dans la colonne Produit, il y a trois cases contenant les nombres suivants pour chaque multiplication : 920, 92 et neuf virgule deux. Deuxième tableau. Dans la colonne Opérations, il y a trois cases contenant respectivement les multiplications suivantes : deux virgule cinq fois cinq, deux virgule cinq fois 50 et deux virgule cinq fois 500. La colonne Estimation est complètement vide. Et dans la colonne Produit, il y a trois cases contenant les nombres suivants pour chaque multiplication : 1 250, 125 et douze virgule cinq.
Poursuivre cette activité en créant d’autres séries d’opérations apparentées. C’est en développant et en utilisant leur sens du nombre que les élèves apprennent à déterminer la position de la virgule dans le produit.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83.
Activité 3 : la marche pour Terry Fox
Présenter le problème suivant aux élèves :
Pour la journée Terry Fox, tous les élèves de l’école participent à une marche. Si les 278 élèves de l’école primaire marchent une distance de 0,9 km chacun, combien de kilomètres en tout auront-ils parcourus?
Permettre aux élèves de choisir une stratégie pour résoudre le problème.
Exemple
Multiplication effectuée à l’aide d’une disposition rectangulaire
J’estime que les élèves auront marché un peu moins de 278 km puisque \(278\; \times \;0,9\; \approx \;278\; \times \;1\). J’effectue la multiplication à l’aide de la disposition rectangulaire. Je décompose 278 en \(200\; + \;70\; + \;8\) et je multiplie chaque terme par 0,9. J’additionne ensuite les produits partiels pour trouver le total.
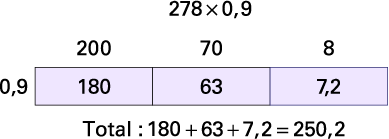
Image Sous la multiplication 278 fois zéro virgule neuf, on trouve un rectangle séparé en trois. À gauche de celui-ci, il y a le chiffre zéro virgule neuf. Sur la première partie du rectangle, il est écrit 180, et au-dessus, il est écrit 200. Sur la deuxième partie, il est écrit 63, et au-dessus, il est écrit 70. Et sur la troisième partie, il est écrit sept virgule deux, et au-dessus, il est écrit huit. Sous le rectangle, il est écrit : Total : 180 plus 63 plus sept virgule deux égale 250 virgule deux.
Poser des questions aux élèves telles que :
- Dans ce cas-ci, est-ce que le produit sera plus grand ou plus petit que le multiplicande? Comment le sais-tu?
- Quel algorithme peut-on utiliser pour résoudre le problème? Pourquoi?
- En comparant les différents algorithmes utilisés, que remarque-t-on?
- Comment peut-on s’assurer que notre calcul soit vraisemblable? Justifie ta réponse.
Les élèves ont marché 250,2 km en tout.
Source : En avant, les maths! 6e année, CM, Nombres, p. 6.
