B2.7 Represent and solve problems involving the multiplication of three-digit whole numbers by decimal tenths, using algorithms.
Activity 1: The Recipe
Share the following situation with students:
A community gathering is being held at the school in one month. There are 120 guests in the school gym. Each class has its responsibilities, and the students in our class are responsible for the food. Deli dishes will be served.
Provide a list of foods that contain mass per serving. Explain to students that each person will eat approximately three servings. Invite students to choose the foods that will be eaten by the guests and use a strategy of their choice to calculate the total mass of each food.
Example
Brie: 30.2 g/slice
Camembert: 28.4 g/slice
Smoked turkey: 89.9 g/slice
White ham: 85.3 g/slice
Grapes: 180.3 g/serving
Crackers: 62.1/serving
Ask students questions such as:
- How much Brie should they order? Smoked turkey? White ham? Grapes? Crackers? How do you know?
- If only 110 guests show up for the event, how much of each food item will they need to prepare? Justify your answer.
- If the supplier does not have smoked turkey in stock, what could students choose instead? How much of each food item will they need to order? Explain your choice.
- Which algorithm can be used to solve the problem? Explain your reasoning.
- When comparing the different algorithms used, what do we notice?
- How can we ensure that our calculations are plausible? Justify your answer.
Activity 2: Estimating the Result of Multiplication
Introduce number strings to support students to understand the impact on the decimal point when multiplying. For example:


Continue this activity by creating other sets of related operations, or having students create them. By developing and using their number sense, students learn to determine the position of the decimal point in the product.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 83.
Activity 3: Walking for Terry Fox
Present the following problem to students:
For Terry Fox Day, all students in the school participate in a walk. If the 278 students in the elementary school walk a distance of 0.9 km each, how many kilometres in total will they have walked?
Allow students to choose a strategy to solve the problem.
Example
Multiplying with an Area Model
I estimated that the students will have walked a little less than 278 km since \(278\; \times \;0.9\; \approx \;278\; \times \;1\). I used an array to multiply. I decomposed 278 into \(200\; + \;70\; + \;8\) and multiply each term by 0.9. I then added the partial products to find the total.
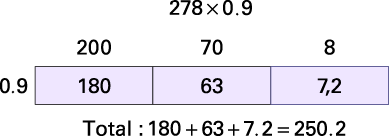
The students walked a total of 250.2 km.
Ask students questions such as:
- In this case, will the product be larger or smaller than the multiplicand? How do you know?
- Which algorithm can be used to solve the problem? Explain your thinking.
- When comparing the different algorithms used, what do we notice?
- How can we ensure that our calculation is plausible? Justify your answer.
Source: translated from En avant, les maths! 6e, CM, Nombres, p. 6.
