B1.2 Lire et représenter des nombres entiers, à l’aide d’outils et de stratégies, y compris de droites numériques horizontales et verticales.
Habileté : lire des nombres entiers
Chaque nombre entier a son opposé, tous deux situés à distance égale de zéro sur la droite numérique. Par exemple, (−1) et 1 sont des nombres entiers opposés et se trouvent à la même distance de zéro.
Les paires de nombres entiers opposés donnent zéro. Par exemple, des paires de nombres entiers comme \((+3)\) et \((-3) = 0\).
Le zéro est défini comme étant neutre, donc ni positif, ni négatif.
Les nombres entiers négatifs sont « inférieurs à zéro ». Zéro se trouve exactement au centre de la droite numérique des nombres entiers; la droite est symétrique autour de zéro.
Sur une droite numérique horizontale, les entiers positifs sont affichés à droite de zéro et les entiers négatifs sont affichés à gauche de zéro.
Sur une droite numérique verticale, les entiers positifs sont affichés au-dessus du zéro et les entiers négatifs sont affichés sous le zéro.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
L’usage le plus connu des nombres entiers négatifs concerne la température. Par exemple, (−3º) signifie 3º au-dessous de 0 degré. Il arrive parfois que les nombres entiers négatifs soient utilisés pour décrire des dettes. Par exemple, si l’on doit 5 $, on peut considérer que l’on a (−5) $. Les nombres négatifs sont parfois utilisés dans les statistiques de hockey et le pointage au golf.
Source : Réduction des écarts de rendement, 9e année, p. 11.
Habileté : représenter des nombres entiers
Les nombres entiers négatifs sont situés à gauche de 0 sur la droite numérique. Ce sont les opposés des nombres entiers positifs, ce qui signifie qu’ils sont situés aussi loin à gauche de 0 que ces derniers le sont à droite de 0. Ainsi, (−5) est exactement à la même distance à la gauche de 0 que 5 l’est à sa droite. Puisque les nombres sont placés en ordre croissant de gauche à droite sur la droite, un nombre entier négatif est donc nécessairement plus petit qu’un nombre entier positif.

Il est possible de représenter les nombres entiers sur une droite numérique verticale qui est semblable à un thermomètre plutôt que sur une droite numérique horizontale. Dans ce cas, les nombres entiers positifs sont au-dessus des nombres entiers négatifs.
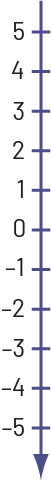
Il est aussi possible d’utiliser des jetons bicolores pour représenter des nombres entiers, une couleur pour représenter les nombres entiers positifs et une autre pour représenter les nombres entiers négatifs. Par exemple, 5 peut être représenté par 5 jetons blancs et (−5) par 5 jetons rouge.

Source : Réduction des écarts de rendement, 9e année, p. 10-11.
Les nombres entiers peuvent être représentés sous forme de points sur une droite numérique ou sous forme de vecteurs (flèches) indiquant l’ordre de grandeur et la direction. Le nombre entier (−5) peut être représenté par un point positionné à 5 unités à gauche du zéro ou 5 unités au-dessous de zéro. Le nombre entier (−5) peut également être représenté comme un vecteur allant de zéro à (−5) sur la droite numérique afin de montrer qu’il a une longueur de 5 unités et se déplace dans le sens négatif.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : nombres entiers
Ensemble des nombres entiers (\(\mathbb{Z}\))
L’ensemble des nombres entiers est composé des nombres naturels (\(\mathbb{N}\)) (0, 1, 2, 3…) et des entiers négatifs ((−1), (−2), (−3)…). On peut donc dire que tous les nombres naturels sont des nombres entiers, mais les nombres entiers ne sont pas tous des nombres naturels. On peut représenter la relation entre les nombres naturels et les nombres entiers par le diagramme de Venn illustré ci-dessous.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 41.
