B1.4 Lire, représenter, comparer et ordonner les nombres décimaux jusqu’aux millièmes, dans divers contextes.
Habileté : lire des nombres décimaux jusqu’aux millièmes
L’apprentissage des nombres décimaux est étroitement lié à la compréhension de la notation décimale. Cette notation est employée couramment, entre autres dans le système international d’unités (SI) et dans le système monétaire. Toutefois, malgré son utilisation fréquente au quotidien et en classe, la notation décimale est loin d’être bien comprise et maîtrisée.
Afin d’explorer l’apprentissage des nombres décimaux, il importe d’examiner la terminologie reliée à ces nombres et à la notation décimale. Un nombre décimal est un nombre qui peut être exprimé en notation décimale avec une partie décimale finie (par exemple, 3,72; 12,135 64). L’ensemble des nombres décimaux inclut tous les entiers, car ces derniers peuvent être exprimés avec une partie décimale (par exemple, \(3\; = \;3,0\)).
Il est intéressant de constater que tous les nombres décimaux peuvent être exprimés sous forme de fractions décimales, c’est-à-dire des fractions dont le dénominateur est une puissance de 10.
Au cycle moyen, l’étude des nombres décimaux est reliée plus particulièrement à l’utilisation de la notation décimale pour exprimer ces nombres. Un nombre exprimé en notation décimale est composé de deux parties, à savoir la partie entière et la partie décimale.
Exemple
Le nombre \(8\frac{1}{8}\) s’écrit en notation décimale 8,125.
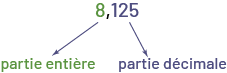
Dans l’enseignement des nombres décimaux et de la notation décimale qui s’y rapporte, on met trop souvent l’accent
sur l’apprentissage de procédures et de règles, plutôt que sur les concepts qui les soutiennent. On empêche ainsi les
élèves de développer une connaissance conceptuelle des nombres décimaux. Des énoncés comme « on peut ajouter des zéros
après la dernière décimale sans changer la quantité, par exemple 2,3 = 2,30 » nuisent à la compréhension de la
quantité représentée par un nombre décimal et leur emploi réduit l’apprentissage des nombres décimaux à une obéissance
à des règles.
Selon les recommandations dans le document intitulé Enseigner et apprendre les
mathématiques : Rapport de la Table ronde des experts en mathématiques de la 4e à la
6e année (Ministère de l’Éducation de l’Ontario, 2004a), un enseignement efficace des mathématiques
doit viser à faire comprendre le sens des concepts enseignés. Puisque la partie décimale d’un nombre n’est, de fait,
qu’une différente façon de représenter une fraction décimale, il est essentiel que les élèves aient une compréhension
solide des fractions et de la valeur de position avant d’être initiés au concept de nombre décimal. En ce qui a trait
à la quantité que représente un nombre décimal, il faut établir des liens entre la partie décimale du nombre et le
concept de fraction. Paradoxalement, l’écriture et la lecture des nombres décimaux s’apparentent davantage à celles
des nombres naturels qu’à celles des fractions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28-30.
L’utilisation de nombres décimaux pour exprimer une quantité répond à un besoin d’exprimer des quantités avec plus de précision.
Exemple
Considérons une diagonale d’un carré dont les côtés mesurent 1 m. Si on tente de décrire la longueur de cette diagonale en utilisant les nombres naturels, on peut dire qu’elle mesure 1 m et « une partie de un mètre ».

Il est possible de donner une mesure plus précise en exprimant cette « partie de un mètre » en notation décimale. En utilisant une règle graduée en décimètres, on peut déterminer que la diagonale mesure environ 1,4 m. On pourrait même obtenir une mesure de 1,41 m avec une règle graduée en centimètres ou 1,414 m avec une règle graduée en millimètres.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 32-34.
Relations de valeur de position
C’est au début du cycle moyen que les élèves étudient pour la première fois la partie décimale d’un nombre. Ils doivent alors approfondir leur compréhension de la valeur de position des chiffres et de la relation entre les valeurs de position. Les nombres décimaux font partie du quotidien et la compréhension des valeurs de position à la droite et à la gauche de la virgule est essentielle.
La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.
Or, il est essentiel que les élèves reconnaissent la position des unités puisque c’est elle qui définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, les centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.
 Image Le
schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le mot
« unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Image Le
schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le mot
« unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les dizaines représentent une quantité dix fois plus grande que l’unité, alors que les dixièmes représentent une quantité dix fois plus petite que l’unité. De même, la centaine est cent fois plus grande que l’unité, alors que le centième est cent fois plus petit que l’unité.
Note : Certains élèves ont l’impression que c’est la virgule qui est au centre du système décimal. Conséquemment, ils ont tendance à appeler la première position à droite de la virgule, la position des unièmes plutôt que des dixièmes.
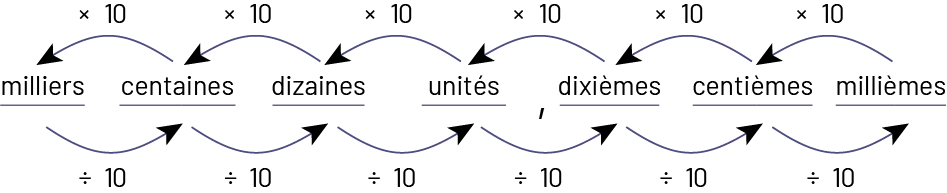
Il est important que les élèves saisissent aussi la relation multiplicative par 10 qui existe entre les valeurs de position adjacentes. Ils ont préalablement développé une compréhension de cette relation dans le cadre de l’étude des nombres naturels, soit que chaque position a une valeur 10 fois plus grande que celle à sa droite et 10 fois plus petite que celle à sa gauche.
Or, cette relation multiplicative est aussi vraie pour les positions décimales.
 Image
Le schéma se présente comme suit, de gauche à droite : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. En haut, chaque mot est relié à son précédent par une flèche courbe au-dessus de laquelle il est
écrit « fois dix ». En bas, chaque mot est relié au suivant par une flèche courbe sous laquelle il est écrit « divisé
par dix ».
Image
Le schéma se présente comme suit, de gauche à droite : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. En haut, chaque mot est relié à son précédent par une flèche courbe au-dessus de laquelle il est
écrit « fois dix ». En bas, chaque mot est relié au suivant par une flèche courbe sous laquelle il est écrit « divisé
par dix ».
Les élèves peuvent en développer une compréhension en effectuant des regroupements à l’aide du matériel de base dix. Il s’agit de démontrer que, tout comme 10 unités donnent 1 dizaine, 10 dixièmes donnent 1 unité et 10 centièmes donnent 1 dixième, et ainsi de suite.
Il arrive fréquemment aux élèves du cycle moyen d’écrire, par exemple, 0,013 pour représenter treize centièmes. Ces élèves tentent de placer 13 dans la colonne des centièmes comme suit.
0 , 0 13
Or, le système décimal ne permet pas d’écrire deux chiffres dans une position. Les élèves doivent reconnaître que 10 centièmes c’est l’équivalent de 1 dixième, ce qui fait que 13 centièmes c’est égal à 1 dixième plus 3 centièmes. On écrit donc 0,13.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 51-53.
Représentation mentale
Pour bien développer le sens du nombre, il est important que les élèves se forment des images des quantités représentées par les nombres. Dans le cas des nombres décimaux, les lire correctement permet de s’en faire une meilleure représentation mentale et de faire appel à leurs connaissances des fractions (par exemple, 0,175 se lit « cent soixante-quinze millièmes » et non pas « zéro virgule cent soixante-quinze »). Il faut inciter les élèves à utiliser plusieurs modèles pour favoriser la création de diverses représentations mentales.
Exemple
 Image Trois nombres sont présentés avec un exemple qui les représentent.Le premier nombre est un
dixième ou zéro
virgule un. Il est représenté par une rangée de dix unités, l’une est rouge et les neuf autres sont vertes. Le
deuxième nombre est 75 sur 100 ou zéro virgule 75. Il est représenté par une grille de 100 unités; 75 sont rouges
et 25 sont blanches. Le troisième nombre est zéro virgule 125. Il est représenté par une grille de 100 unités. Douze
unités et demie sont rouges, les autres sont blanches.
Image Trois nombres sont présentés avec un exemple qui les représentent.Le premier nombre est un
dixième ou zéro
virgule un. Il est représenté par une rangée de dix unités, l’une est rouge et les neuf autres sont vertes. Le
deuxième nombre est 75 sur 100 ou zéro virgule 75. Il est représenté par une grille de 100 unités; 75 sont rouges
et 25 sont blanches. Le troisième nombre est zéro virgule 125. Il est représenté par une grille de 100 unités. Douze
unités et demie sont rouges, les autres sont blanches.
Lors de la représentation de nombres décimaux à l’aide de modèles, il y a une adaptation à faire, car ces mêmes modèles étaient utilisés jusqu’alors pour représenter d’autres concepts (par exemple, la languette représentait une dizaine de cubes). Les élèves doivent comprendre que l’unité a changé. Dans le premier des trois exemples précédents, c’est l’objet au complet qui représente l’unité (le tout); dans le deuxième et le troisième, c’est le grand carré au complet qui représente l’unité (le tout).
Les élèves doivent aussi se former une représentation mentale de nombres décimaux supérieurs à un. À la lecture d’un tel nombre décimal, ils doivent se représenter mentalement la quantité qu’il représente en interprétant les deux parties qui le composent : la partie entière et la partie décimale. Par exemple, ils doivent reconnaître que le nombre 8,245 représente 8 entiers et une partie d’un autre entier identique. Ils peuvent alors visualiser une quantité entre 8 et 9.

Avec le temps, les élèves sont en mesure de se représenter mentalement la quantité en tenant compte du contexte. Par exemple, dans une situation où il est question d’un article qui coûte 197,98 $, l’élève qui reconnaît que 197,98 $ c’est un peu plus que 197 $ peut ensuite visualiser ou concevoir que, dans ce contexte, le montant de 197,98 $ peut être représenté approximativement par 10 billets de 20 $.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 36-37.
Habileté : représenter des nombres décimaux jusqu’aux millièmes
Les élèves doivent apprendre non seulement à représenter les nombres décimaux de diverses façons, mais aussi à les reconnaître sous leurs multiples représentations. Ces habiletés les aident à établir des liens entre les nombres, leurs représentations et les quantités qu’ils représentent. Dans certains cas, l’utilisation de modèles facilite la construction des représentations.
La figure suivante illustre diverses façons de représenter vingt-cinq centièmes concrètement, semi-concrètement, symboliquement et à l’aide de mots, et suggère, par les expressions 0,25 $, 0,25 kg, 0,25 h et 0,25 cm, différents contextes pour son utilisation. Les élèves développent une meilleure compréhension des nombres si on leur demande régulièrement et dans une variété de situations de passer d’une représentation à une autre.
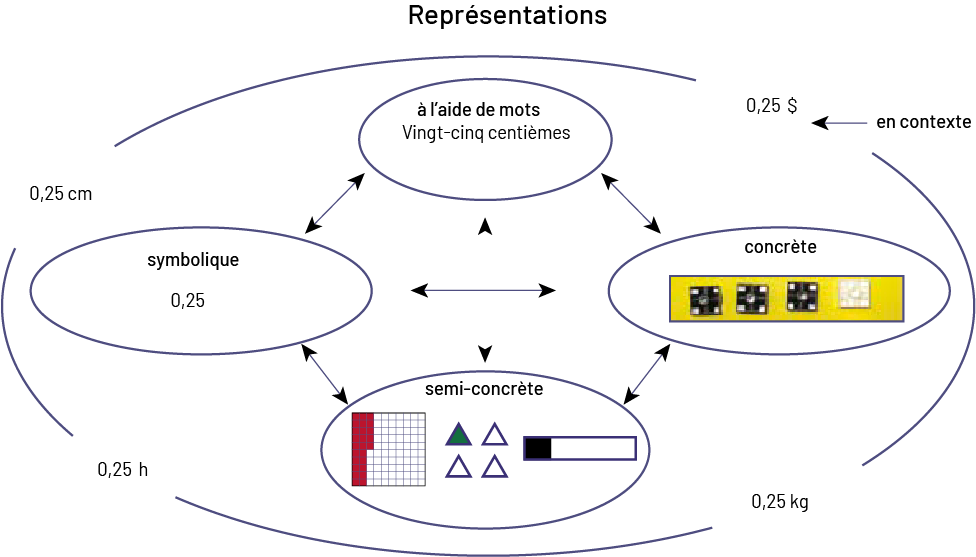 Image Le schéma s’intitule « Représentations ».En haut, en bas, à gauche et à droite, il y a
quatre arcs qui, sans se toucher, forment une espèce d’ovale. Entre l’arc du haut et l’arc de droite, il est écrit zéro virgule 25 dollar. L’expression « En contexte » pointe vers la somme. Entre l’arc de droite et l’arc du bas, il est écrit zéro virgule 25 kilogramme. Entre l’arc du bas et l’arc de gauche, il est écrit zéro virgule 25 heure. Et entre l’arc de gauche et l’arc du haut, il est écrit zéro virgule 25 centimètres. Sous chaque creux d’arc apparaissent différents termes, disposés en forme de losange, chacun écrit dans un ovale. En haut, l’ovale contient l’expression « à l'aide de mots », et « vingt-cinq centièmes » écrit en lettres. À droite, l’ovale contient le mot « concrète » ainsi qu’une photo montrant un carré blanc et trois carrés noirs. En bas, l’ovale contient le mot « semi-concrète » ainsi que trois images : la première montre 25 carrés rouges et 75 carrés blancs dans une grille de cent unités, la deuxième montre un triangle vert et trois triangles blancs, et la troisième montre le quart d’une barre coloré de noir avec le reste en blanc. Et à gauche, l’ovale contient le mot « symbolique » et zéro virgule 25. Tous les termes sont reliés les uns aux autres par des flèches à double sens.
Image Le schéma s’intitule « Représentations ».En haut, en bas, à gauche et à droite, il y a
quatre arcs qui, sans se toucher, forment une espèce d’ovale. Entre l’arc du haut et l’arc de droite, il est écrit zéro virgule 25 dollar. L’expression « En contexte » pointe vers la somme. Entre l’arc de droite et l’arc du bas, il est écrit zéro virgule 25 kilogramme. Entre l’arc du bas et l’arc de gauche, il est écrit zéro virgule 25 heure. Et entre l’arc de gauche et l’arc du haut, il est écrit zéro virgule 25 centimètres. Sous chaque creux d’arc apparaissent différents termes, disposés en forme de losange, chacun écrit dans un ovale. En haut, l’ovale contient l’expression « à l'aide de mots », et « vingt-cinq centièmes » écrit en lettres. À droite, l’ovale contient le mot « concrète » ainsi qu’une photo montrant un carré blanc et trois carrés noirs. En bas, l’ovale contient le mot « semi-concrète » ainsi que trois images : la première montre 25 carrés rouges et 75 carrés blancs dans une grille de cent unités, la deuxième montre un triangle vert et trois triangles blancs, et la troisième montre le quart d’une barre coloré de noir avec le reste en blanc. Et à gauche, l’ovale contient le mot « symbolique » et zéro virgule 25. Tous les termes sont reliés les uns aux autres par des flèches à double sens.
Représentations concrètes
Pour bien comprendre les nombres décimaux, il est important que les élèves puissent les représenter concrètement à l’aide de matériel de manipulation (par exemple, jetons, matériel de base dix). Malheureusement, les élèves du cycle moyen n’ont pas toujours l’occasion d’explorer les nombres à l’aide de ce genre de matériel. Conséquemment, leur connaissance des nombres décimaux repose souvent sur la représentation symbolique et ne témoigne pas d’une solide compréhension de ces nombres. Avant d’entreprendre l’enseignement des nombres décimaux, il est important d’amener les élèves à utiliser du matériel de manipulation pour décrire des parties d’un tout représentées par une fraction décimale (par exemple, \(\frac{3}{{10}}\), \(\frac{{12}}{{100}}\)).
Exemple
 Image
Deux rangées de réglettes de la même longueur sont placées l’une sous l’autre. La première est formée de cinq
réglettes pourpres, tandis que la deuxième est formée de dix réglettes roses. La première réglette rose est surélevée
pour se coller contre la première réglette pourpre et illustrer qu’une réglette rose équivaut à une demi-réglette
pourpre. Sous la photo, il est écrit : un dixième d’un tout.
Image
Deux rangées de réglettes de la même longueur sont placées l’une sous l’autre. La première est formée de cinq
réglettes pourpres, tandis que la deuxième est formée de dix réglettes roses. La première réglette rose est surélevée
pour se coller contre la première réglette pourpre et illustrer qu’une réglette rose équivaut à une demi-réglette
pourpre. Sous la photo, il est écrit : un dixième d’un tout.
Lorsque les élèves ont pris l’habitude de bien reconnaître les dixièmes, les centièmes et les millièmes, on peut utiliser du matériel concret pour présenter la notation décimale. Voici une représentation concrète des nombres 2,4 et 0,70.
 Image Deux photos sont placées côte à côte.La première photo montre deux rangées de réglettes placées l’une sous l’autre. La première rangée est faite de deux longues réglettes orange et d’une réglette pourpre plus courte. La deuxième rangée est faite de deux réglettes orange et de quatre petites réglettes bleues. Sous la photo, il est écrit : L’unité est la réglette orange. Deux virgule quatre réglettes. La deuxième photo montre un géoplan dont une portion est encadrée. Sous la photo, il est écrit : L’unité est la surface du géoplan. Zéro virgule 70 du géoplan.
Image Deux photos sont placées côte à côte.La première photo montre deux rangées de réglettes placées l’une sous l’autre. La première rangée est faite de deux longues réglettes orange et d’une réglette pourpre plus courte. La deuxième rangée est faite de deux réglettes orange et de quatre petites réglettes bleues. Sous la photo, il est écrit : L’unité est la réglette orange. Deux virgule quatre réglettes. La deuxième photo montre un géoplan dont une portion est encadrée. Sous la photo, il est écrit : L’unité est la surface du géoplan. Zéro virgule 70 du géoplan.
Le matériel de base dix est un outil par excellence pour représenter un nombre décimal, puisqu’il met en évidence la relation multiplicative par 10 entre la valeur de position des chiffres qui le composent. Cependant, il est très important de toujours définir clairement la pièce qui constitue l’unité en fonction de laquelle les autres pièces seront définies. Lors de l’étude des nombres naturels, le petit cube était généralement associé à l’unité. Cependant, si on choisit la languette comme unité, le petit cube représente alors un dixième de languette.
Exemple
Le petit cube représente 0,1 d’une languette.

Si on choisit la planchette comme unité, le petit cube représente alors un centième de planchette et la languette représente un dixième de planchette.
Exemple
Le petit cube représente 0,01 d’une planchette.

Si on choisit le gros cube comme unité, le petit cube représente alors un millième du gros cube, la languette représente un centième du gros cube et la planchette représente un dixième du gros cube.
Les photos ci-dessous montrent la représentation sur un tapis de valeur de position de différents nombres en fonction de différentes unités.



La monnaie peut aussi être utilisée lors de l’exploration des nombres décimaux. Cependant, il importe de n’utiliser que les pièces de 1 $, de 10 ¢ et de 1 ¢ puisque leur valeur respecte la relation multiplicative par 10. Une représentation en utilisant la monnaie est plus abstraite que celle en utilisant le matériel de base dix puisque la relation multiplicative par 10 est basée sur la valeur de la pièce et non sur sa taille. Les élèves peuvent identifier la pièce de 1 $ comme étant l’unité. La pièce de 10 ¢ représente alors un dixième de l’unité (0,1 de dollar) et la pièce de 1 ¢, un centième de l’unité (0,01 de dollar). De la relation multiplicative par 10, les regroupements se forment en respectant la valeur de position : 10 pièces de un centième de dollar équivalent à 1 pièce de un dixième de dollar et 10 pièces de un dixième de dollar équivalent à 1 pièce de 1 $.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 57-62.
Représentations semi-concrètes
Les élèves peuvent aussi développer le sens des nombres décimaux et des pourcentages en les représentant de façon semi-concrète. Par exemple, un disque partagé en 10 parties égales permet de représenter des dixièmes et un disque partagé en 100 parties égales permet de représenter des centièmes.
Exemples
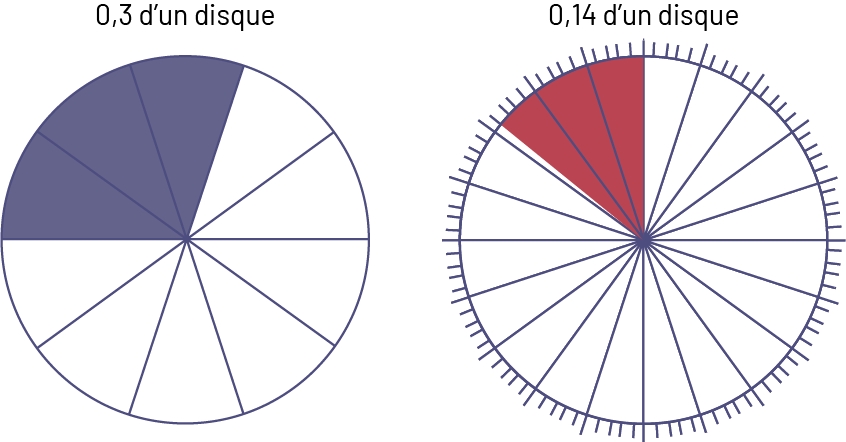 Image Deux disques de la même grosseur sont placés côte à côte.Le premier disque est divisé en dix parties égales. Trois parties sont colorées en bleu. Au-dessus, il est écrit zéro
virgule trois d’un disque.Le deuxième disque est divisé en vingt parties égales, et chaque partie est subdivisée en cinq. Deux parties et
quatre cinquièmes d’une partie sont colorés en rouge. Au-dessus, il est écrit zéro virgule quatorze d’un disque.
Image Deux disques de la même grosseur sont placés côte à côte.Le premier disque est divisé en dix parties égales. Trois parties sont colorées en bleu. Au-dessus, il est écrit zéro
virgule trois d’un disque.Le deuxième disque est divisé en vingt parties égales, et chaque partie est subdivisée en cinq. Deux parties et
quatre cinquièmes d’une partie sont colorés en rouge. Au-dessus, il est écrit zéro virgule quatorze d’un disque.
Des bandes et des grilles séparées en 10, en 100 ou en 1 000 parties égales peuvent aussi être utilisées pour représenter des nombres décimaux.
Exemple

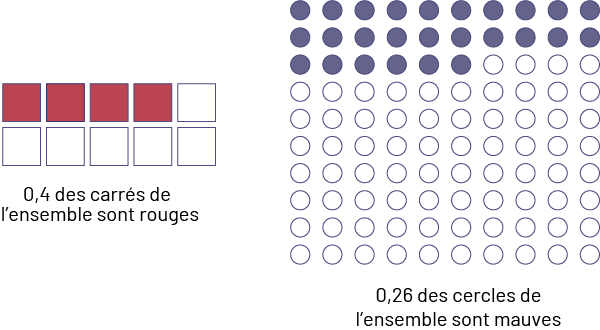
Il est important aussi que les élèves utilisent des modèles d’ensembles pour représenter des nombres décimaux.
Exemples
 Image
Deux images sont placées côte à côte. La première image montre deux rangées de cinq cubes. Les quatre premiers cubes
sont rouges tandis que les six autres sont blancs. En dessous, il est écrit : zéro virgule quatre carrés de l’ensemble
sont rouges. La deuxième image montre dix rangées de dix cercles. Les 26 premiers cercles sont mauves tandis que les
autres sont blancs. En dessous, il est écrit : zéro virgule 26 des cercles de l’ensemble sont mauves.
Image
Deux images sont placées côte à côte. La première image montre deux rangées de cinq cubes. Les quatre premiers cubes
sont rouges tandis que les six autres sont blancs. En dessous, il est écrit : zéro virgule quatre carrés de l’ensemble
sont rouges. La deuxième image montre dix rangées de dix cercles. Les 26 premiers cercles sont mauves tandis que les
autres sont blancs. En dessous, il est écrit : zéro virgule 26 des cercles de l’ensemble sont mauves.
Pour développer un bon sens du nombre, il est important que les élèves explorent différentes représentations d’une même quantité. Par exemple, on peut les inviter à représenter 0,50 de plusieurs façons sur une grille de \(10\; \times \;10\).
Exemples

Cinq grilles de 100 unités sont placées côte à côte.
Dans la première grille, un carré sur deux est coloré de bleu.
Dans la deuxième grille, une rangée sur deux est orangée.
Dans la troisième grille, les 25 carrés du coin supérieur gauche et les 25 carrés du coin inférieur droit sont verts.
Dans la quatrième grille, qui est divisée à la diagonale, une moitié est colorée en orange.
On peut imaginer la cinquième grille comme si elle était séparée en quatre quadrants pour faciliter la description. Chaque quadrant est divisé en deux sur la diagonale, et une partie sur deux dans chaque quadrant est colorée de rouge.
On peut aussi les inviter à utiliser différentes représentations semi-concrètes pour représenter un nombre donné.
Exemples
Voici, trois représentations de 0,3.
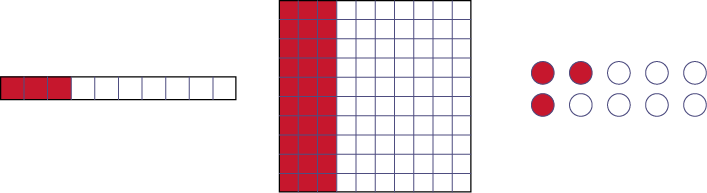 Image Trois images sont présentées côte à côte.La première image montre une languette de dix unités; trois rouges et sept blanches. La deuxième image montre une grille de 100 unités; les trois premières colonnes sont rouges et les sept suivantes sont blanches. La troisième image montre deux rangées de cinq cercles; les deux premiers cercles de la première rangée sont rouges, le premier cercle de la deuxième rangée est rouge et les sept autres cercles sont blancs.
Image Trois images sont présentées côte à côte.La première image montre une languette de dix unités; trois rouges et sept blanches. La deuxième image montre une grille de 100 unités; les trois premières colonnes sont rouges et les sept suivantes sont blanches. La troisième image montre deux rangées de cinq cercles; les deux premiers cercles de la première rangée sont rouges, le premier cercle de la deuxième rangée est rouge et les sept autres cercles sont blancs.
Les élèves ont appris à se servir d’une droite numérique pour situer des nombres naturels et pour compter jusqu’à de grands nombres par intervalles. Ils peuvent aussi l’utiliser pour situer les nombres décimaux. Pour ce faire, les élèves doivent comprendre comment subdiviser les intervalles et reconnaître à quoi correspond chaque intervalle.
Droite numérique graduée pour représenter des dixièmes et des centièmes
 Image
Une droite numérique est graduée de zéro à un et subdivisée par centièmes. Le point zéro virgule un est indiqué sur la
droite. Une légende indique la distance mesurant zéro virgule un ainsi que la distance mesurant zéro virgule zéro un.
Image
Une droite numérique est graduée de zéro à un et subdivisée par centièmes. Le point zéro virgule un est indiqué sur la
droite. Une légende indique la distance mesurant zéro virgule un ainsi que la distance mesurant zéro virgule zéro un.
Droite numérique graduée pour représenter des centièmes et des millièmes
 Image
Une droite numérique est graduée de zéro à zéro virgule un. Le point zéro virgule un est indiqué sur la droite. Une
légende indique la distance mesurant zéro virgule zéro un ainsi que la distance mesurant zéro virgule zéro zéro un.
Image
Une droite numérique est graduée de zéro à zéro virgule un. Le point zéro virgule un est indiqué sur la droite. Une
légende indique la distance mesurant zéro virgule zéro un ainsi que la distance mesurant zéro virgule zéro zéro un.
Droite numérique graduée pour situer les nombres 5,2 et 5,32

Représentations symboliques
L’écriture conventionnelle des nombres décimaux est une représentation symbolique de ces concepts. Pour représenter symboliquement des nombres décimaux, une virgule est intégrée dans l’écriture du nombre afin de séparer la partie entière de la partie décimale.
Exemple
Trois et cent vingt-cinq millièmes

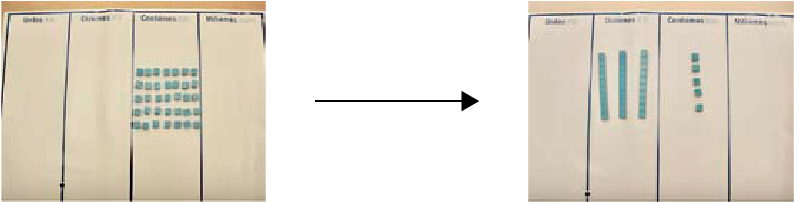
L’écriture des nombres décimaux nécessite la compréhension du concept de regroupement. Ainsi le nombre « trente-cinq centièmes », après regroupements, correspond à 3 dixièmes et 5 centièmes d’où l’écriture du chiffre 3 dans la position des dixièmes et du chiffre 5 dans la position des centièmes, soit 0,35.
 Image
Sur le premier tapis de position, il y a 35 unités sous la colonne des centièmes. Sur le deuxième tapis de position,
il y a trois languettes de dix unités sous la colonne des dixièmes, ainsi que cinq unités sous la colonne des
centièmes.
Image
Sur le premier tapis de position, il y a 35 unités sous la colonne des centièmes. Sur le deuxième tapis de position,
il y a trois languettes de dix unités sous la colonne des dixièmes, ainsi que cinq unités sous la colonne des
centièmes.
Cette relation entre l’écriture d’un nombre décimal et les regroupements peut être comprise en explorant les nombres décimaux à l’aide de représentations concrètes et semi-concrètes qui permettent de « voir » les regroupements. Par exemple, les élèves peuvent conclure, en comptant, que les figures suivantes représentent respectivement 9 millièmes, 11 millièmes et 101 millièmes.
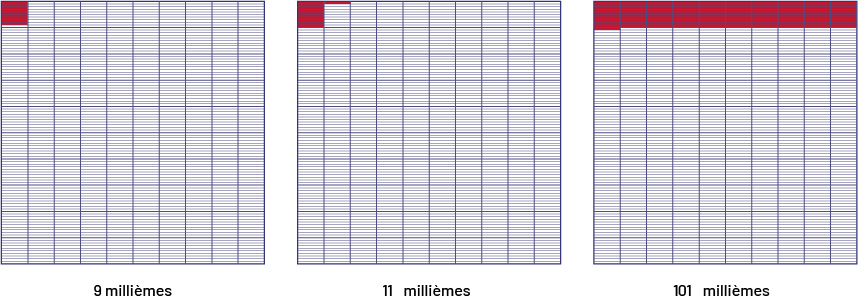 Image Trois grilles de millièmes sont placées côte à côte.Dans la première grille, 90 unités dans le premier carré de 100 sont colorées en rouge, ce qui représente neuf millièmes. Dans la deuxième grille, un carré de cent complet et dix unités de cent sont colorés en rouge, ce qui représente 11 millièmes. Et dans la troisième grille, dix carrés de cent et dix unités de cent sont colorés en rouge, ce qui représente 101
millièmes.
Image Trois grilles de millièmes sont placées côte à côte.Dans la première grille, 90 unités dans le premier carré de 100 sont colorées en rouge, ce qui représente neuf millièmes. Dans la deuxième grille, un carré de cent complet et dix unités de cent sont colorés en rouge, ce qui représente 11 millièmes. Et dans la troisième grille, dix carrés de cent et dix unités de cent sont colorés en rouge, ce qui représente 101
millièmes.
Leur connaissance des fractions leur permet de représenter ces quantités par \(\frac{9}{{1\;000}}\), \(\frac{{11}}{{1\;000}}\) et \(\frac{{101}}{{1\;000}}\), et leur compréhension du concept de valeur de position leur permet de reconnaître que la première fraction, exprimée en notation décimale, s’écrit 0,009. Cependant, il n’est pas évident que les deux autres s’écrivent 0,011 et 0,101. Par exemple, pour comprendre que 0,011 représente bien 11 millièmes, il est utile de démontrer à l’aide d’un regroupement que 11 millièmes est équivalent à « 1 centième plus 1 millième ».
Il est important de faire la distinction entre le chiffre dans la position des millièmes et la quantité de millièmes dans le nombre. Ainsi, dans le nombre 0,011, le chiffre dans la position des millièmes est 1, mais il y a 11 millièmes dans le nombre. Dans le nombre 0,101, le chiffre dans la position des millièmes est également un 1, mais ce nombre est composé de 101 millièmes. Ainsi, si on veut que les élèves identifient le chiffre dans la position des dixièmes dans un nombre donné (par exemple, 2,35), il faut poser la question « Quel chiffre est dans la position des dixièmes dans le nombre 2,35? » plutôt que « Combien de dixièmes y a-t-il dans le nombre 2,35? »
Représentations à l’aide de mots
La façon dont les élèves apprennent à lire les nombres décimaux peut avoir une incidence sur leur compréhension. Si on leur montre à lire les nombres 0,7 et 0,75 en disant « zéro virgule sept » et « zéro virgule sept cinq », ou « zéro virgule soixante-quinze », on laisse de côté le sens de la notation. Cette façon de lire un nombre décimal ne constitue qu’une énumération successive des symboles qui composent le nombre, tout comme ce serait le cas si on lisait le nombre 123 en disant « un, deux, trois ». Cependant, si on insiste pour lire ces nombres en disant « sept dixièmes » et « soixante-quinze centièmes », on met l’accent sur le sens de la notation. Cette façon de lire les nombres décimaux donne la possibilité aux élèves de visualiser les 7 parties de 10 et les 75 parties de 100 et a l’avantage de rappeler la correspondance entre les nombres décimaux et les fractions décimales correspondantes. Elle permet aussi de se référer à un nombre décimal par son nom.
Il importe que le personnel enseignant modèle en tout temps cette façon de lire les nombres décimaux. Les nombres 12,34 et 1 013,7 se lisent respectivement « douze et trente-quatre centièmes » et « mille treize et sept dixièmes ». On remarque que lors de la lecture d’un nombre décimal, la partie entière est lue comme s’il s’agissait d’un nombre naturel, le mot « et » (et non « virgule ») sert de liaison entre les deux parties, et la partie décimale est lue en fonction de la valeur de position du chiffre situé à l’extrême droite dans le nombre.
Note : Il arrive que certains élèves, en lisant, confondent les termes dizaine et dixième, ainsi que centaine et centième, à cause de leur similarité phonétique.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 65-69.
Habileté : comparer et ordonner des nombres décimaux jusqu’aux millièmes
La relation d’ordre est basée sur la comparaison de nombres. Une des grandes forces de la notation décimale, c’est la rapidité avec laquelle il est possible, grâce au concept de valeur de position, de comparer et d’ordonner des quantités. Par exemple, il est beaucoup plus facile de comparer les nombres \(\frac{1}{8}\) et \(\frac{3}{{40}}\) lorsqu’ils sont exprimés en notation décimale, soit 0,125 et 0,075.
En général, les élèves ont peu de mal à comparer des nombres décimaux ayant le même nombre de décimales (par exemple, \(0,341 < 0,462\)). Ils ont plus de difficulté à comparer des nombres ayant un nombre différent de décimales (par exemple, 1,34 et 1,275). Certains ont tendance à comparer ces nombres sans la virgule (par exemple, \(134 < 1\;275\)) et conclure que \(1,34 < 1,275\). D’autres arrivent à la même conclusion erronée en comparant seulement les nombres à droite de la virgule (par exemple, \(34 < 275\)).
La relation d’ordre doit être abordée en comparant des nombres décimaux dans des situations contextualisées. Par exemple : « Rémi a fait un saut de 3,55 m et Samantha en a effectué un de 3,7 m. Lequel des deux a réussi le plus long saut? » Les élèves peuvent répondre et justifier leur choix s’ils comprennent la valeur de position. La droite numérique est un modèle visuel puissant pour comparer des nombres décimaux. Pour placer 3,7 sur une droite numérique, les élèves peuvent représenter les dixièmes de 3,0 à 4,0. Pour situer 3,55, ils doivent diviser l’intervalle entre 3,5 et 3,6 en dix parties égales, chaque espace représentant un centième. Ils peuvent alors conclure que \(3,55 < 3,7\), donc que Samantha a effectué un plus long saut que Rémi.
 Image Une droite numérique est graduée de trois virgule zéro à quatre virgule zéro par intervalles de dixièmes L’intervalle entre trois virgule cinq et trois virgule six est gradué par centièmes. Au-dessus de la droite se trouve le chiffre trois virgule 55 qui pointe avec une flèche à l’endroit correspondant sur la droite. Il y a également le chiffre trois virgule sept qui pointe à l’endroit correspondant sur la droite.
Image Une droite numérique est graduée de trois virgule zéro à quatre virgule zéro par intervalles de dixièmes L’intervalle entre trois virgule cinq et trois virgule six est gradué par centièmes. Au-dessus de la droite se trouve le chiffre trois virgule 55 qui pointe avec une flèche à l’endroit correspondant sur la droite. Il y a également le chiffre trois virgule sept qui pointe à l’endroit correspondant sur la droite.
Les élèves qui ont acquis un bon sens du nombre peuvent aussi comparer 3,55 m et 3,7 m en remarquant d’abord qu’ils représentent deux sauts supérieurs à 3 m. Ensuite, ils peuvent comparer les dixièmes pour remarquer que le premier nombre compte 5 dixièmes, soit 5 décimètres, tandis que le deuxième en compte 7.

Le deuxième saut est donc plus long que le premier. Les élèves peuvent aussi, après avoir comparé les unités, penser à 3,7 comme étant 3,70, soit 3 mètres et 70 centimètres. Le nombre 3,55 représente 3 mètres et 55 centimètres. Le saut de 3,7 m est donc plus long que le saut de 3,55 m.
Traditionnellement, on enseignait une procédure où il fallait ajouter un zéro à la fin de 3,7 pour donner deux nombres ayant un même nombre de décimales. Il fallait ensuite comparer les parties décimales, soit 55 et 70, pour conclure que 3,70 était plus grand que 3,55. Certes, l’enseignement de la méthode était accompagné d’une explication, mais on mettait tellement l’accent sur la procédure que l’explication et le concept étaient vite perdus. Il n’est pas surprenant que les jeunes répondent souvent de façon erronée à ce genre de questions. Par exemple, lors d’un test international réalisé auprès d’élèves de 6e année, 87 % ont indiqué que 6 987 est plus grand que 6 879, alors que seulement 52 % ont conclu que 1,05 est plus grand que 1,015 (Brissiaud, 1998). Les élèves qui comprennent le concept de valeur de position n’ont pas besoin d’appliquer une procédure pour comparer des nombres décimaux.
Les problèmes ouverts, qui offrent plus d’une réponse et qui suscitent la réflexion, permettent aux élèves d’approfondir leur compréhension des relations d’ordre. Par exemple :
- Déterminer trois nombres décimaux situés entre \(\frac{3}{{40}}\) et \(\frac{1}{8}\).
- Déterminer trois nombres décimaux situés entre 0,555 et 0,623.
- Déterminer deux nombres situés à un millième de 2,869.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 54-55.
Habileté : lire, représenter, comparer et ordonner les nombres décimaux dans divers contextes
Le contexte est l’ensemble des informations entourant une situation donnée. Pour bien saisir le sens de la quantité représentée par un nombre décimal, les élèves doivent l’analyser dans son contexte. Comme une fraction, un nombre décimal représente une partie d’un tout. L’ampleur de la quantité représentée par un nombre décimal dépend donc entièrement de la grandeur du tout.
Il faut insister sur le fait que le contexte aide à préciser la quantité représentée. Par exemple, s’il est question de 2,347, les élèves comprennent que ce nombre représente 2 fois une unité quelconque et \(\frac{{347}}{{100}}\) de la même unité. Mais, si on précise qu’il s’agit de 2,347 m, ils peuvent se faire une image de la quantité en contexte.
Or, dans certaines situations, il est important de reconnaître que les nombres décimaux ne se rapportent pas au même tout.
Exemple
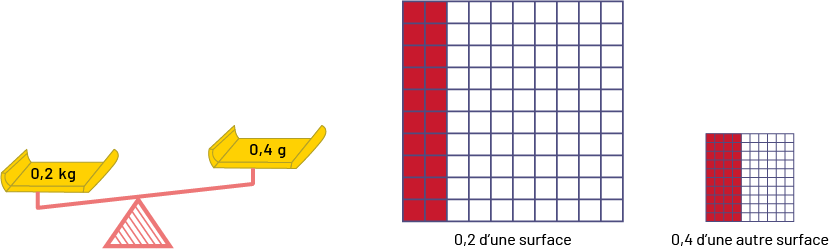 Image Trois images sont placées côte à côte.La première image montre une balance où du côté gauche, il y a une charge de zéro virgule deux kilogrammes, et du côté droit, la charge est de zéro virgule quatre grammes. La balance penche du côté gauche. La deuxième image montre une grille de cent. Les deux premières colonnes sont colorées en rouge. En dessous, il est écrit : zéro virgule deux d’une surface.La troisième image montre une plus petite grille de cent. Les quatre premières colonnes sont colorées en rouge. En dessous, il est écrit : zéro virgule quatre d’une autre surface.
Image Trois images sont placées côte à côte.La première image montre une balance où du côté gauche, il y a une charge de zéro virgule deux kilogrammes, et du côté droit, la charge est de zéro virgule quatre grammes. La balance penche du côté gauche. La deuxième image montre une grille de cent. Les deux premières colonnes sont colorées en rouge. En dessous, il est écrit : zéro virgule deux d’une surface.La troisième image montre une plus petite grille de cent. Les quatre premières colonnes sont colorées en rouge. En dessous, il est écrit : zéro virgule quatre d’une autre surface.
Dans ces exemples, même si le nombre 0,2 est inférieur au nombre 0,4 (\(0,2 < 0,4\)), 0,2 kg est une masse plus grande que 0,4 g, tout comme 0,2 du gros carré est une surface plus grande que 0,4 du petit carré.
En outre, sans contexte, il est parfois impossible de porter un jugement critique sur l’importance de la quantité représentée par un nombre décimal. Par exemple, l’achat par un enfant d’une voiture miniature à 8,34 $ peut être considéré comme coûteux par ses parents, alors que l’enfant peut trouver que c’est une aubaine pour une voiture de collection. Plus les élèves sont confrontés à différentes situations mathématiques en contexte, plus ils acquièrent de connaissances et plus ils peuvent porter des jugements critiques avisés.
Les gros titres de journaux fournissent souvent des sujets de discussion qui peuvent aider les élèves à comprendre et à interpréter les nombres décimaux.
Exemples
- Baisse de 13,7 millions de dollars dans le budget municipal
- Nouveau record mondial, une pomme de 13,455 kg!
Au cours d’un échange en groupe classe, le personnel enseignant peut poser des questions qui aident les élèves à analyser les titres indiqués ci-dessus.
Exemples
- Est-ce important de préciser les 0,455 kg dans la masse de la pomme? Pourquoi?
- À première vue, 13,7 millions de dollars, c’est beaucoup d’argent, mais est-ce un montant important dans le budget?
- Comment un nombre comme 13,7 peut-il représenter un si gros montant d’argent?
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 40-41.
Connaissance : nombre décimal
Ensemble des nombres décimaux (𝔻)
L’ensemble des nombres décimaux est formé des nombres qui peuvent être exprimés sous forme décimale avec une partie décimale finie (par exemple, 3,72; (−5,1); 0; (–7,0); 12,135 64). Cet ensemble inclut tous les entiers, car ils peuvent être exprimés avec une partie décimale (par exemple, \(3\; = \;3,0\)). Il inclut aussi certaines fractions, comme \(\frac{2}{5}\) et \(\frac{3}{{16}}\), puisque \(\frac{2}{5}\; = \;0,4\) et \(\frac{3}{{16}}\; = \;0,187\;5\). Cependant, un grand nombre de fractions sont exclues, comme \(\frac{1}{3}\) et \(\frac{7}{{11}}\), car leur développement décimal nécessite un nombre infini de décimales (\(\frac{1}{3}\; = \;0,333\;33\)… et \(\frac{7}{{11}}\; = \;0,636\;363\)…).
Il est intéressant de constater que tous les nombres décimaux peuvent être exprimés sous forme de fraction dont le dénominateur est une puissance de 10. (Les puissances de 10 sont 1, 10, 100, 1 000… On inclut 1 comme puissance de 10, car, par définition, \(10^{0} \; = \;1\).)
Exemples
\(3,72\; = \;3\frac{{72}}{{100}}\; = \;\frac{{372}}{{100}}\)
\(5\; = \;5,1\; = \;\frac{5}{1}\)
Puisque les nombres naturels sont tous des nombres entiers et que les nombres entiers sont tous des nombres décimaux, on peut représenter la relation entre les ensembles de nombres par le diagramme de Venn ci-dessous.

Note : Il n’existe pas d’ensemble de nombres à virgule. L’appellation nombre à virgule signifie simplement que l’expression du nombre contient une virgule. Ainsi, un nombre à virgule peut être un nombre décimal (par exemple, 0,45), un nombre périodique (par exemple, 0,333…) ou un nombre irrationnel (par exemple, 3,141 5…).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 42.
Connaissance : millièmes
La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.

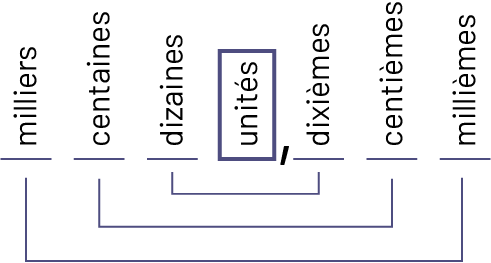
La position des unités définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, les centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.
 Image
Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le
mot « unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Image
Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le
mot « unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les millièmes représentent une quantité mille fois plus petite que l’unité.
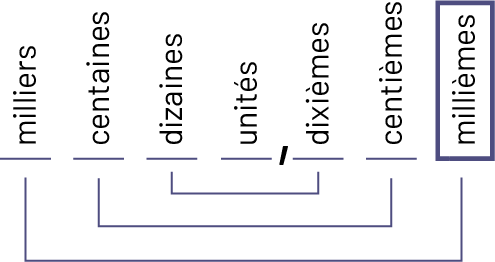 Image Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. Le mot « millièmes » est encadré. Les mots « milliers » et « millièmes » sont réunis par un
trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Image Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. Le mot « millièmes » est encadré. Les mots « milliers » et « millièmes » sont réunis par un
trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 51.
