B1.4 Read, represent, compare, and order decimal numbers up to thousandths, in various contexts.
Skill: Reading Decimal Numbers up to Thousandths
Learning decimal numbers is closely related to understanding decimal notation. Decimal notation is commonly used in the International System of Units (SI) and in the monetary system, among other things. However, despite its frequent use in everyday life and in the classroom, decimal notation is far from being well understood and mastered.
In order to explore learning about decimal numbers, it is important to examine the terminology related to these numbers as well to decimal notation. A decimal number is a number that has a decimal point, such as 3.72 or 12.13564. The part before the decimal point represents a whole number amount, and the part after the decimal point represents a value that is less than one. Integers can also be expressed with decimal numbers (for example, 3 = 3.0).
It is interesting to note that all decimal numbers can be expressed as decimal fractions, that is, fractions whose denominator is a power of 10.
In the junior grades, the study of decimal numbers is related specifically to the use of decimal notation to express numbers. A number expressed in decimal notation is composed of two parts, the integer part and the decimal part.
Example
The number \(8\frac{1}{4}\) is written as 8.25 when represented as a decimal number.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 28-30.
In teaching decimal numbers and related decimal notation, the focus is too often on learning procedures and rules, rather than the concepts that support understanding them. This singular focus prevents students from developing conceptual knowledge of decimal numbers. Statements such as "you can add zeros after the last decimal place without changing the quantity, for example, undermine understanding the quantity represented by a decimal number and reduces learning about decimal numbers to rule following.
Research emphasizes that effective mathematics instruction should focus on developing an understanding of the concepts, skills, and procedures being taught. Decimal numbers are a way of representing numbers with a decimal point and decimal fractions are fractions in which the denominator is equal to 10 or multiples of 10. For these reasons, it is essential that students have a solid understanding of fractions and place value before they are introduced to decimal numbers. In terms of the quantity that a decimal number represents, connections must be made between the decimal part of the number and the concept of a fraction. Paradoxically, the writing and reading of decimal numbers are more similar to those of whole numbers than to fractions.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 30.
The use of decimal numbers to express a quantity allows greater precision.
Example
Consider a diagonal of a square with sides measuring 1 m. If we try to describe the length of this diagonal using whole numbers, we can say that it measures 1 m and "part of one metre".

A more accurate measurement can be given by expressing this "part of a metre" in decimal notation. Using a ruler graduated in decimetres, we can determine that the diagonal is about 1.4 m. One could even obtain a measurement of 1.41 m with a centimetre ruler or 1.414 m with a millimetre ruler.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 32-34.
Place Value Relationships
The beginning of the junior grades is the first time that students study the decimal part of a number. They will continue to deepen their understanding of place values and the relationship between the place values to the right of the decimal point. Decimal numbers are part of everyday life and understanding the place values to the right and left of the decimal point is essential.
The decimal point plays a significant role when interpreting the value of a decimal number. It separates the integer part from the decimal part, and thus indicates the position of the ones.
It is essential that students recognize the position of the ones unit, since it is this unit that defines the whole, from which the tenths, hundredths and thousandths are formed on the one hand, and the tens, hundreds and thousands on the other. We can therefore say that the ones unit, identified by the decimal point, is at the heart of the decimal system.

This recognition of the role of the ones unit is evidenced by the names given to the place values of the digits on either side of the ones. Tens represent a quantity ten times greater than one, while tenths represent a quantity ten times smaller than one. Similarly, one hundred is a hundred times larger than one, while one hundredth is a hundred times smaller than one.
Note: Some students are under the impression that the decimal point is the centre of the decimal system. As a result, they tend to call the first position to the right of the decimal point "oneths" rather than tenths.
It is important that students also grasp the x10 multiplicative relationship that exists between adjacent place values. They have previously developed an understanding of this relationship in the study of whole numbers, such that each position has a value 10 times greater than the one to its right and 10 times smaller than the one to its left.
This multiplicative relationship is also true for decimal places.

Students can develop an understanding of this by doing groupings using base ten materials. The idea is to demonstrate that just as 10 ones yield 1 ten, 10 tenths yield 1 one and 10 hundredths yield 1 tenth, and so on.
It is common for junior students to write 13 in the hundredths column as follows.
0 . 0 13
However, the decimal system does not allow two digits to be written in one position. The students must recognize that 10 hundredths make 1 tenth, which makes 13 hundredths equal to 1 tenth plus 3 hundredths. Therefore, we write 0.13.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 51-53.
Mental Representation
In order to develop number sense, it is important that students can visualize the quantities represented by numbers. In the case of decimal numbers, reading them correctly allows students to form better mental representations and to draw on their knowledge of fractions (for example, 0.175 reads "one hundred and seventy-five thousandths", not "zero point one hundred and seventy-five"). Students should be encouraged to use multiple models to support the creation of various mental representations.
Example

When representing decimal numbers using models, there is an adjustment to be made, as these same models were previously used to represent other concepts (for example, the rod represented ten ones). Students need to understand that the whole has changed. In the first of the three examples above, the train represents the whole; in the second example, the flat represents the whole.
Students must also form a mental representation of decimal numbers greater than one. When reading such a decimal number, they must mentally picture the quantity it represents by interpreting the two parts that make up the number: the integer part and the decimal part. For example, they must recognize that the number 8.245 represents 8 integers and part of another identical integer. They can then visualize a quantity between 8 and 9.

Over time, students are able to mentally picture the quantity in context. For example, in a situation involving an item that costs $197.98, a student who recognizes that $197.98 is more than $197.00 and a little less than $198.00 can then visualize or conceive that, in this context, the amount of $197.98 can be represented approximately by 10 $20 bills.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 36-37.
Skill: Representing Decimal Numbers up to Thousandths
Students need to learn how to represent decimal numbers in a variety of ways, and recognize them in their multiple representations. These skills help them make connections between numbers, their representations, and the quantities they represent. In some cases, the use of models facilitates the construction of representations.
The following figure illustrates various ways to represent twenty-five hundredths concretely, visually (semi-concretely), symbolically, and with words. It also demonstrates how 0.25 is used in different contexts. Students develop a better understanding of numbers if they are regularly asked in a variety of situations to move from one representation to another.
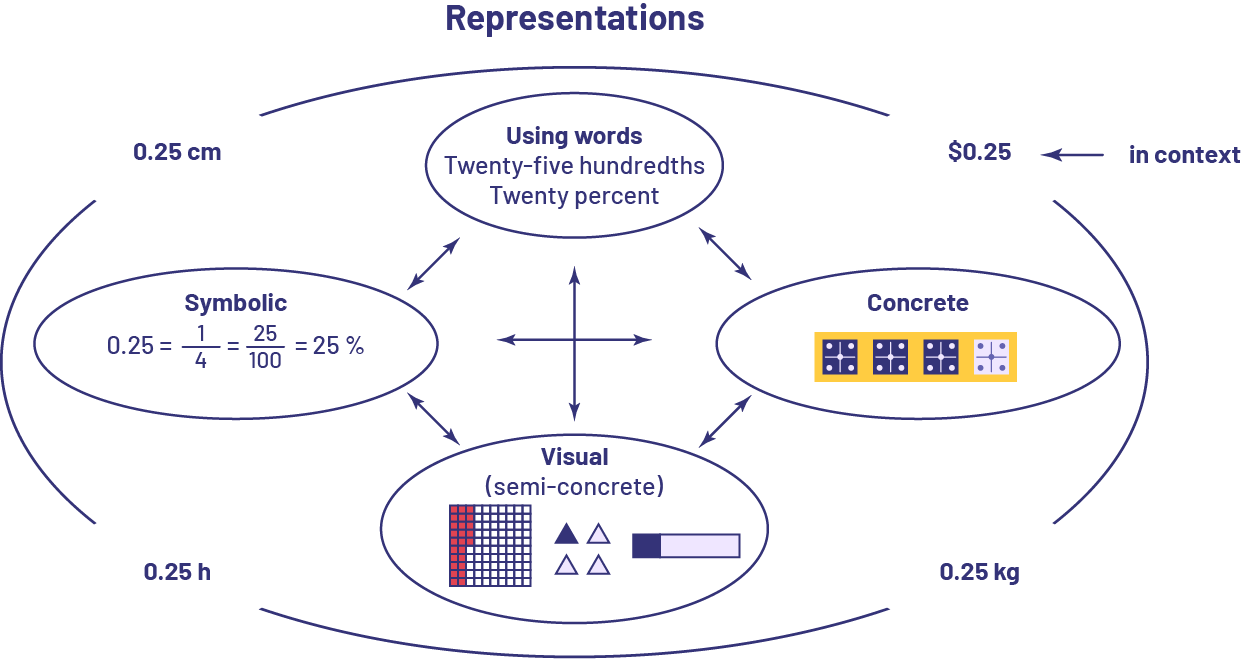
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 57-58.
Concrete Representations
In order to fully understand decimal numbers, it is important that students be able to represent them concretely using manipulatives (for example, using counters or base ten blocks). Therefore, in the junior grades, students should have the opportunity to explore numbers using these materials to build conceptual understanding. Before beginning to teach decimal numbers, it is important to have students use manipulatives to show the parts of a whole that is represented by a decimal fraction (for example, \(\frac{3}{10}\)).
Example

Once students have become accustomed to recognizing tenths, hundredths, and thousandths, concrete materials can be used to introduce decimal notation, such as the following concrete representations of 2.4 and 0.70.

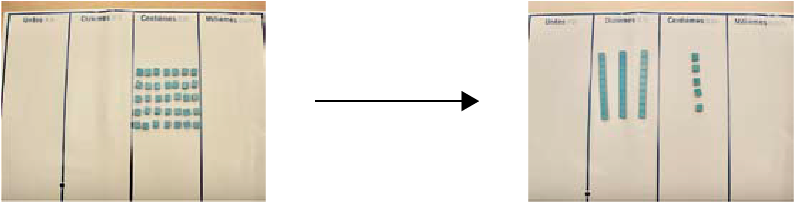
Base ten materials are excellent tools to represent a decimal number, since they highlight the x10 multiplicative relationship between the place values of digits. However, it is very important to always clearly define the piece that constitutes the whole (unit) according to which the other pieces will be defined. When studying whole numbers, the small cube was usually associated with ones. However, if we choose the rod to be the whole, then the small cube represents one tenth.
Example
The small cube represents 0.1 of a rod.

If we choose the flat as the whole, then the small cube represents one hundredth of a flat and the rod represents one tenth of a flat.
Example
The small cube represents 0.01 of a flat.

If we choose the large cube as the whole, then the small cube represents one thousandth of the large cube, the rod represents one hundredth of the large cube and the flat represents one tenth of the large cube. For example:


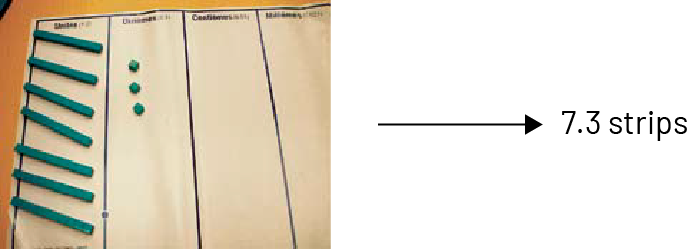
Money can also be used when exploring decimal numbers. However, it is important to use only the $1, 10¢, and 1¢ coins since their value respects the x10 multiplicative relationship of the base ten system. A representation using coins is more abstract than one using base ten material since the x10 relationship is based on the value of the coin and not its size. Students may identify the $1 coin as the whole. In this case, the 10¢ coin then represents one-tenth of the whole (0.1 of a dollar) and the 1¢ coin represents one-hundredth of the whole (0.01 of a dollar). From the x10 multiplicative relationship means that 10 coins of one-hundredth of a dollar are equivalent to 1 coin of one-tenth of a dollar and 10 coins of one-tenth of a dollar are equivalent to 1 coin of $1.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 57-62.
Visual (Semi-Concrete) Representations
Students can also develop a conceptual understanding of decimal numbers and percents by representing them in visual or semi-concrete ways. For example, a disk divided into 10 equal parts can represent tenths and a disk divided into 100 equal parts can represent hundredths.
Examples

Paper strips and grids separated into 10, 100, or 1000 equal parts can also be used to represent decimal numbers.
Example

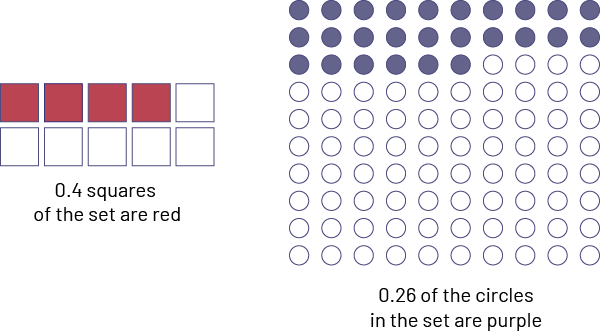
It is also important that students use set models to represent decimal tenths.
Examples
To develop good number sense, it is important that students explore different representations of the same quantity. For example, they can be encouraged to represent 0.5 in a variety of ways on a \(10 \times 10\) grid.
Examples

They can also be asked to use different visual representations to represent a given number.
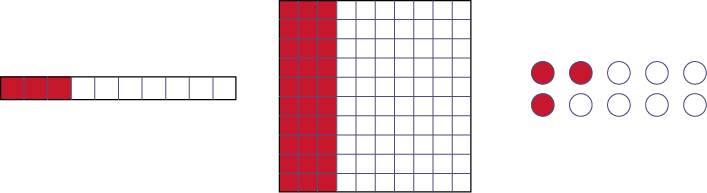
Examples
The following are three representations of 0.3:
Students have learned to use a number line to locate whole numbers and to count to large numbers in intervals. They can also use them to locate decimal numbers. To do this, students need to understand how to partition the intervals and recognize what values each interval corresponds to.
Number line to represent tenths and hundredths:

Number line to represent hundredths and thousandths:

Number line to locate the numbers 5.2 and 5.32:

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 65-67.
Symbolic Representation
To symbolically represent decimal numbers, a decimal point is used to separate the integer part from the decimal part.
Example
Three and one hundred twenty-five thousandths
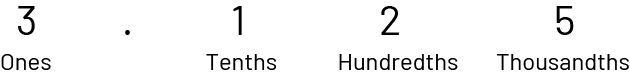
Writing decimal numbers requires an understanding of the concept of regrouping. Thus the number "thirty-five hundredths", after regrouping, corresponds to 3 tenths and 5 hundredths, hence the writing of the number 3 in the tenths position and the number 5 in the hundredths position, or 0.35.
This relationship between writing a decimal number and groupings of 10 can be understood by exploring decimal numbers using concrete and visual representations that allow one to "see" the groupings. For example, students can conclude that the following models represent 9 thousandths, 11 thousandths, and 101 thousandths respectively.
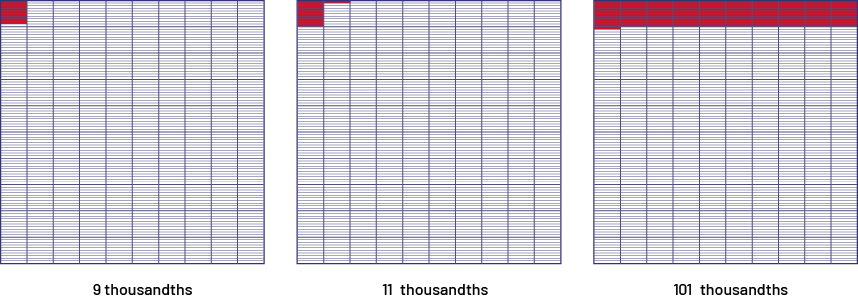
Their knowledge of fractions enables students to represent these quantities by \(\frac{9}{1000}\), \(\frac{11}{1000}\) and \(\frac{101}{1000}\), and their understanding of the concept of place value enables them to recognize that the first fraction, expressed in decimal notation, is written 0.009. However, it's not obvious that the other two are written as 0.011 and 0.101. For example, to understand that 0.011 represents 11 thousandths, it is useful to demonstrate with a grouping that 11 thousandths is equivalent to "1 hundredth plus 1 thousandth".
It is important to distinguish between the number in the thousandths position and the amount of thousandths in the number. For example, in the number 0.011, the digit in the thousandths position is 1, but there are 11 thousandths in the number. In the number 0.101, the digit in the thousandths position is also a 1, but this number is 101 thousandths. If we want students to identify the digit in the tenths position in a given number (for example, 2.35), we need to ask the question "What digit is in the tenths position in the number 2.35?" rather than "How many tenths are in the number 2.35?
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 67-69.
Representations Using Words
How students learn to read decimal numbers can affect their understanding. If they are taught to read the numbers 0.7 and 0.75 by saying "zero point seven" and "zero point seven five," or "zero point seventy-five," the meaning of the notation is left out. This way of reading a decimal number is merely a sequential listing of the symbols that make up the number, just as it would be if one were to read the number 123 by saying "one, two, three." However, if we insist on reading these numbers as "seven tenths" and "seventy-five hundredths," we are emphasizing the meaning of the notation. This way of reading decimal numbers gives students the opportunity to visualize the 7 parts of 10 and the 75 parts of 100 and has the advantage of reminding them of the correspondence between decimal numbers and the corresponding decimal fractions. It also allows students to refer to a decimal number by its name.
It is important that teachers model this way of reading decimal numbers at all times. The numbers 12.34 and 1013.7 read "twelve and thirty-four hundredths" and "one thousand thirteen and seven tenths" respectively. Note that when reading a decimal number, the integer part is read as if it were a whole number, the word "and" (not "period") serves as a link between the two parts, and the decimal part is read according to the place value of the far right digit in the number.
Note: Some students may confuse the terms ten and tenth or hundred and hundredth when reading because of their phonetic similarity.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 69.
Skill: Comparing and Ordering Decimal Numbers to Thousandths
Ordering is based on the comparison of numbers. One of the great strengths of decimal notation is the speed with which it is possible, through the concept of place values, to compare and order quantities. For example, it is easy to compare the numbers 0.125 and 0.075 expressed in decimal notation.
In general, students have little difficulty comparing decimal numbers with the same number of decimal places (for example, \(0.341 < 0.462\)). They have more difficulty comparing numbers with different numbers of decimal places (for example, 1.34 and 1.275). Some tend to compare these numbers without the decimal point (for example, \(134 < 1\;275\)) and conclude that \(1.34 < 1.275\). Others reach the same erroneous conclusion by comparing only the numbers to the right of the decimal point (for example, \(34 < 275\)).
Learning to compare decimal numbers is best done in contextualized situations. For example: "Remi did a jump of 3.55 m and Samantha did one of 3.7 m. Which of the two had the longer jump?" Students can respond and justify their choice if they understand place value. The number line is a powerful visual model for comparing decimal numbers. To place 3.7 on a number line, students can represent tenths from 3.0 to 4.0. To place 3.55, they must partition the interval between 3.5 and 3.6 into tenths, with each space representing one hundredth. They can then conclude that 3.55 < 3.7, so Samantha has taken a longer jump than Remi.

Students who have acquired good number sense can also compare 3.55 m and 3.7 m by first noticing that they represent two jumps greater than 3 m. Then they can compare the tenths to notice that the first number has 5 tenths, or 5 decimetres, while the second has 7.

The second jump is therefore longer than the first. Students can also, after comparing units, think of 3.7 as 3.70, or 3 metres and 70 centimetres. The number 3.55 represents 3 metres and 55 centimetres. The 3.7 m jump is therefore longer than the 3.55 m jump.
Traditionally, a procedure was taught whereby one was instructed to add a zero to the end of 3.7 to result in two numbers with the same number of decimal places. Then the decimal parts, 55 and 70, were compared to conclude that 3.70 was greater than 3.55. Although the teaching of this method might have been accompanied by an explanation, so much emphasis was placed on the procedure that the explanation and the concept were not paramount. Not surprisingly, students often answered such questions incorrectly. For example, in an international test of Grade 6 students, 87% reported that 6,987 is greater than 6,879, while only 52% concluded that 1.05 is greater than 1.015 (Brissiaud, 1998). This finding illustrates that it is important that students understand the concept of place value and do not need to rely on a procedure that may let them down when comparing decimal numbers.
Open-ended problems, which offer more than one answer and are thought-provoking, allow students to deepen their understanding of ordering decimal numbers. For example:
- Determine three decimal numbers between \(\frac{3}{{40}}\) and \(\frac{1}{8}\).
- Determine three decimal numbers between 0.555 and 0.623.
- Determine two numbers within one thousandth of 2.869.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 54-55.
Skill: Reading, Representing, Comparing and Ordering Decimal Numbers in Various Contexts
Context is all the information surrounding a given situation. To understand the meaning of the quantity represented by a decimal number, students must analyze it in its context. Like a fraction, a decimal number represents a part of a whole. The magnitude of the quantity represented by a decimal number is therefore entirely dependent on the magnitude of the whole.
Emphasize that the context helps clarify the quantity represented. For example, if 2.347 is the number being considered, students understand that this number represents 2 ones. But, if it is 2.347 m that is being considered, they can form a picture of the quantity in context which is 2 metres plus a third more.
It is important to recognize when two decimal numbers are not referencing the same whole, such as in the following two examples:
Example
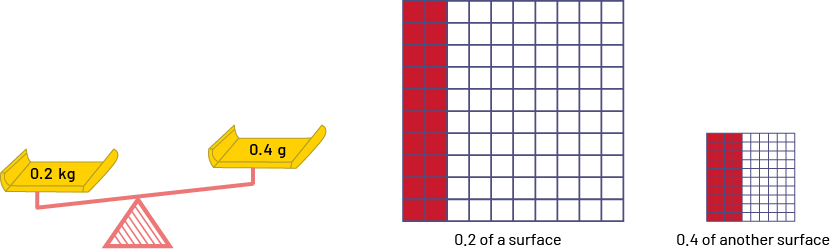
In these examples, even though the number 0.2 is less than the number 0.4 (\(0.2 < 0.4\)), 0.2 kg is a larger mass than 0.4 g, just as 0.2 of the large square is a larger area than 0.4 of the small square.
Furthermore, without context, it is sometimes impossible to make a critical judgment about the size of the quantity represented by a decimal number. For example, a child's purchase of a toy car for $8.34 may be considered expensive by his or her parents, while the child may find it a bargain for a collectible car. The more students are exposed to different mathematical situations in context, the more knowledge they gain and the more informed critical judgments they can make.
Headlines often provide topics for discussion that can help students understand and interpret decimal numbers. For example:
- 13.7 million decrease in municipal budget
- New world record, an apple of 13.45 kg!
During a class discussion, teachers can ask questions like the questions below that will support students in analyzing the headlines.
Examples
- Is it important to specify the 13.45 kg in the mass of the apple? Why or why not?
- At first glance, $13.7 million is a lot of money, but is it a significant amount in the budget?
- How can a number like 13.7 represent such a large amount of money?
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 40-41.
Knowledge: Decimal Number
Decimal numbers are representations of numbers that have a decimal point (for example, 3.72; 0; 12.13564). This set includes all integers, because they can be expressed with a decimal part (for example, 3 = 3.0). It also includes all fractions (for example, \(\frac{2}{5}\; = \;0.4\), \(\frac{3}{{16}}\; = \;0.187\;5\), ( \(\frac{1}{3}\; = \;0.333\;3 \ldots \;{\rm{and}}\;\frac{7}{{11}}\; = \;0.636\; 363 \ldots \)). In Grade 6, students will learn to distinguish between terminating and repeating decimal numbers.
It is interesting to note that all decimal numbers can be expressed as a fraction whose denominator is a power of 10. (The powers of 10 are 1, 10, 100, 1,000… We include 1 as a power of 10 because, by definition, \(10^{0} \; = \;1\)
Examples
\(3.72 = 3\frac{72}{100} = 3\frac{372}{100}\)
\(5\; = \;5.0\; = \;\frac{5}{1}\)
Since all whole numbers are integers and all integers can be represented as decimal numbers, we can represent the relationship between the different types of numbers with the Venn diagram below.

Note: There is no set of decimal numbers. A decimal number is an expression of the number with a decimal point.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 42.
Knowledge: Thousandths
The decimal point plays a significant role in decimal notation. It separates the whole part from the decimal part.

The position of the ones defines the whole according to which are formed on the one hand the tenths, the hundredths and the thousandths and on the other hand the tens, the hundreds and the thousands. It can therefore be said that the ones, identified by the decimal point, is at the heart of the decimal system.
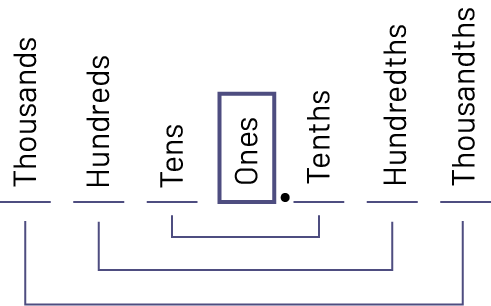
This recognition of the role of the ones is highlighted by the names given to the place value of the digits on either side of the ones. Thus, thousandths represent a quantity one thousand times smaller than the ones.
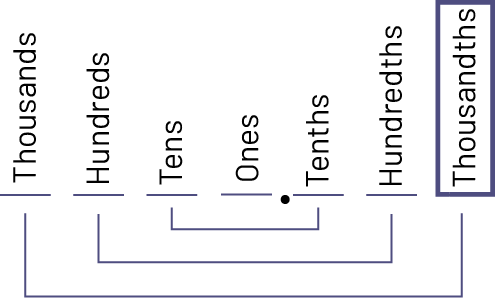
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 51.
