À vue d'oeil...

B2.10 Diviser des nombres naturels par des fractions propres, à l’aide d’une variété d’outils et de stratégies.

Habileté : diviser des nombres naturels par des fractions propres, à l’aide d’une variété d’outils et de stratégies

---

L’exploration de la division, comme celle des autres opérations, doit miser sur les représentations concrètes et semi-concrètes et non sur les algorithmes. Les élèves peuvent alors réactiver leurs connaissances antérieures et saisir le sens de l’opération. Afin de comprendre une division, il est essentiel d’examiner le sens de la division et la nature des nombres qui la composent. Une division a le sens de partage lorsqu’on cherche la taille des groupes; elle a le sens de groupement lorsqu’on cherche le nombre de groupes.

Ainsi, la division d’un nombre naturel par une fraction (par exemple, \(2\; \div \;\frac{1}{3}\)) se représente bien en utilisant le sens de groupement. Dans ce cas, la fraction est le diviseur.

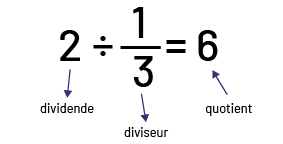
Par exemple, si on a 2 réglisses et que l’on veut remettre à chaque enfant \(\frac{1}{3}\) d’une réglisse, on procède à une division puisqu’il faut séparer une quantité (2 réglisses) en des quantités égales (\(\frac{1}{3}\) de réglisse) pour déterminer le nombre de quantités égales ou de groupes qui peuvent être créés (6 enfants recevront \(\frac{1}{3}\) de réglisse chacun). Dans ce cas, il est important de reconnaître que le quotient exprime un nombre de sections, soit des tiers et non une quantité d’objets (réglisses).

Image Trois ensembles de réglisses. Le premier ensemble, qui comporte deux réglisses, pointe avec une flèche vers le deuxième ensemble, qui comporte six réglisses placées deux par deux. Le premier paquet de deux pointe avec une flèche vers la troisième réglisse du troisième ensemble, qui comporte six réglisses alignées et numérotées.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 79-82.

Dans le cas d’une division d’un nombre naturel par une fraction, la division prend généralement le sens de groupement. Ainsi, l’analogie de la soustraction répétée est de mise puisqu’il s’agit de séparer des parties.

Par exemple, dans la division de 2 par \(\frac{1}{4}\)(\(2\; \div \;\frac{1}{4}\)), en faisant \(2\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\), on peut créer 8 groupes de \(\frac{1}{4}\). Cependant, le groupe créé est plutôt abstrait puisqu’il s’agit d’un groupe qui est une fraction d’un tout. Les questions « Combien de \(\frac{1}{4}\) peuvent être créés avec 2 touts? » et « Combien de fois \(\frac{1}{4}\) va-t-il dans 2? » peuvent aider à se représenter l’opération.

En début d’apprentissage, il est possible d’explorer des situations avec des fractions unitaires (par exemple, \(4\; \div \;\frac{1}{3}\; = \;12\); \(2\; \div \;\frac{1}{5}\; = \;10\); \(3\; \div \;\frac{1}{4}\; = \;12\)) avant d’aborder les opérations ayant une fraction non unitaire. Dans les deux situations, il est préconisé que le quotient soit un nombre naturel (par exemple, \(6\; \div \;\frac{3}{5}\; = \;10\); \(6\; \div \;\frac{2}{3}\; = \;9\)).

Exemple

\(4\; \div \;\frac{1}{3}\; = \;12\)

Modèle de surface

Combien de morceaux de \(\frac{1}{3}\) de tarte peuvent être offerts si on dispose de 4 tartes?

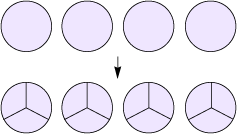
Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 101.

Modèle de longueur

La vidéo suivante montre la division d’un nombre naturel par une fraction à l’aide d’un modèle de longueur.

Exemple

\(6\; \div \;\frac{3}{5}\; = \;10\)

Modèle de surface

Afin de créer un dallage, chaque équipe a besoin de l’équivalent des \(\frac{3}{5}\) des carrés d’une feuille. Combien d’équipes peuvent effectuer la tâche si on dispose de 6 feuilles?

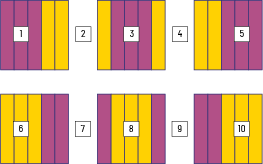
Image Six carrés sont disposés en deux rangées de trois. Ils sont tous divisés en cinq parts égales qui forment des rectangles verticaux. Premier carré : Les trois premiers rectangles sont pourpres et les deux autres sont jaunes. Le chiffre un est placé sur le deuxième rectangle. Le chiffre deux est placé entre le premier et le deuxième carré. Deuxième carré : Le premier et le dernier rectangle sont jaunes et les trois rectangles du centre sont pourpres. Le chiffre trois est placé sur le troisième rectangle. Le chiffre quatre est placé entre le deuxième et le troisième carré. Troisième carré : les deux premiers rectangles sont jaunes tandis que les trois autres sont pourpres. Le chiffre cinq est placé sur le quatrième rectangle. Quatrième carré : les trois premiers rectangles sont jaunes et les deux derniers sont pourpres. Le chiffre six est placé sur le deuxième rectangle. Le chiffre sept est placé entre le quatrième et le cinquième carré. Cinquième carré : le premier et le dernier rectangle sont pourpres et les trois rectangles du centre sont jaunes. Le chiffre huit est placé sur le troisième rectangle. Le chiffre neuf est placé entre le cinquième et le sixième carré. Sixième carré : Les deux premiers rectangles sont pourpres et les trois derniers sont jaunes. Le nombre dix est placé sur le quatrième rectangle.

Modèle de longueur

Une enseignante a une corde de 6 m et veut la couper en sections de \(\frac{3}{5}\) de mètre chacune. Combien de sections pourra-t-elle créer?

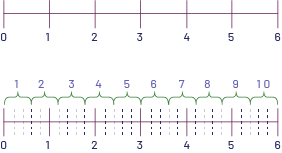
Image Deux droites numériques graduées de zéro à six sont placées l’une sous l’autre. La première ne présente que les chiffres de zéro à six. La deuxième les présente aussi mais possède également des marques d’intervalles de zéro virgule deux en pointillé. Au-dessus, l'accolade un regroupe zéro à zéro virgule six. L’accolade deux regroupe zéro virgule six à un virgule deux. L’accolade trois regroupe un virgule deux à un virgule huit. L’accolade quatre regroupe un virgule huit à deux virgule quatre. L’accolade cinq regroupe deux virgule quatre à trois. L’accolade six regroupe trois à trois virgule six. L’accolade sept regroupe trois virgule six à quatre virgule deux. L’accolade huit regroupe quatre virgule deux à quatre virgule huit. L’accolade neuf regroupe quatre virgule huit à cinq virgule quatre. Et l’accolade dix regroupe cinq virgule quatre à six.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 102.