B2.10 divide whole numbers by proper fractions, using appropriate tools and strategies
Skill: Dividing Whole Numbers by Proper Fractions, Using Appropriate Tools and Strategies
The exploration of division, like that of other operations, must rely on concrete and semi-concrete representations and not on algorithms. Students can then reactivate their prior knowledge and grasp the meaning of the operation. In order to understand division, it is essential to examine the meaning of the division and the nature of the numbers that make up the division. A division has the meaning of sharing when we look for the size of the groups; it has the meaning of grouping when we look for the number of groups.
Thus, dividing a whole number by a fraction (for example, \(2\; \div \;\frac{1}{3}\)) is well represented using grouping. In this case, the fraction is the divisor.
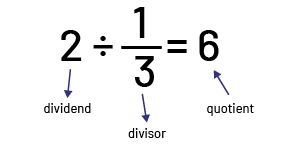
For example, if we have 2 licorice chews and we want to give \(\frac{1}{3}\) of the licorice to each child, we are doing a division since we need to separate one quantity (2 licorice chews) into equal quantities (\(\frac{1}{3}\) of the licorice) to determine the number of equal quantities or groups that can be created (6 children will receive \(\frac{1}{3}\) of the licorice each). In this case, it is important to recognize that the quotient expresses a number of sections, namely, thirds, not a quantity of objects (licorice chews).
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p 79-82.
In the case of a division of a whole number by a fraction, division usually takes on the quotative meaning. Thus, the analogy of repeated subtraction is in order since it involves separating parts.
For example, in dividing 2 by \(\frac{1}{4}\)(\(2\; \div \;\frac{1}{4}\)), doing \(2\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4} \; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{4}\; - \;\frac{1}{ 4}\), we can create 8 groups of \(\frac{1}{4}\). However, the group created is rather abstract since it is a group that is a fraction of a whole. The questions "How many \(\frac{1}{4}\) can be created with 2 wholes?" and "How many times does \(\frac{1}{4}\) go in 2?" can help visualize the operation.
At the beginning of learning, it is possible to explore situations with unit fractions (for example, \(4\; \div \;\frac{1}{3}\; = \;12\); \( 2\; \div \;\frac{1}{5}\; = \;10\); \(3\; \div \;\frac{1}{4}\; = \;12\)) before discussing operations with a non-unit fraction. In both situations, it is recommended that the quotient be a whole number (for example, \(6\; \div \;\frac{3}{5}\; = \;10\); \(6\; \div \;\frac{2}{3}\; = \;9\)).
Example
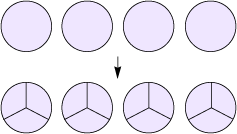
\(4\; \div \;\frac{1}{3}\; = \;12\)
Area Model
How many pieces of \(\frac{1}{3}\) pie can be offered if 4 pies are available?
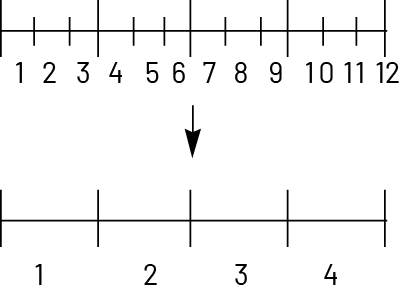
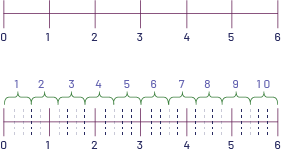
Linear Model
Mathieu wraps gifts in small boxes. He needs \(\frac{1}{3}\) of tape to create a decorative bow. If there are 4 meters of ribbon, how many loops can it create?
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 101.
Example
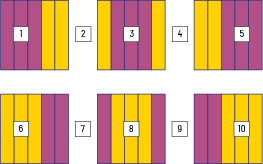
\(6\; \div \;\frac{3}{5}\; = \;10\)
Area Model
In order to create a tessellation, each team needs the equivalent of \(\frac{3}{5}\) squares on a sheet. How many teams can complete the task if we have 6 sheets?
Linear Model
A teacher has a 6m rope and wants to cut it into sections of \(\frac{3}{5}\;\)meters each. How many sections will she be able to create?
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 102.