B2.11 Représenter et résoudre des problèmes relatifs à la division de nombres décimaux jusqu’aux millièmes par un nombre naturel égal ou inférieur à 10, à l’aide d’outils et de stratégies appropriés.
Habileté : représenter et résoudre des problèmes relatifs à la division de nombres décimaux jusqu’aux millièmes par un nombre naturel égal ou inférieur à 10
Au cours de leur apprentissage, les élèves ont appris qu’une division comme \(12\; \div \;3\) s’effectue selon un contexte où l’on crée des groupes de 3 éléments (sens de groupement) ou selon celui où l’on crée 3 groupes égaux (sens de partage). Ces deux contextes existent aussi en présence d’une division d’un nombre décimal par un nombre naturel.
Ainsi, ayant compris ces deux sens de la division avec les nombres naturels, les élèves peuvent reconnaître que la situation selon laquelle on doit répartir équitablement 23,50 $ entre 5 amis revêt un sens de partage et qu’elle peut être représentée par \(23,50\; \div \;5\), division dont le quotient représente la grandeur d’un groupe (nombre de dollars que reçoit un ami). Elles et ils peuvent aussi reconnaître que la situation où il s’agit de verser 23,50 litres de jus dans des contenants de 5 litres revêt un sens de groupement et qu’elle peut aussi être représentée par \(23,50\; \div \;5\). Cependant, dans ce cas, le quotient représente le nombre de groupes (nombre de contenants remplis).
Par la suite, peu importe la situation donnée (partage ou groupement), les élèves peuvent estimer que le quotient est environ 5 et ils peuvent utiliser une stratégie afin de déterminer que le quotient est égal à 4,70 $ (sens partage) ou à 4,7 pichets remplis (sens groupement).
La nature fractionnaire d’un nombre décimal a pour effet de rendre l’interprétation des quantités dans une division plus difficile qu’avec des nombres naturels comme en témoigne le tableau suivant.
| Cellule vide | Partage | Groupement |
|---|---|---|
| Sens du quotient | On cherche le nombre d’éléments dans chaque groupe. | On cherche le nombre de groupes. |
| Problème | Des élèves s’engagent à faire 12,8 km de marche, et ce, en 4 jours. Combien de kilomètres doivent-ils faire quotidiennement s’ils souhaitent parcourir la même distance chaque jour? | Pierre veut faire une randonnée de 12,8 km en parcourant 4 km par heure. Combien d’heures lui faudra-t-il pour réaliser cette randonnée? |
| Opération | \(12,8\; \div \;4\) | \(12,8\; \div \;4\) |
| Question à poser | On partage les 12,8 km en 4 étapes de même longueur (4 groupes). Quelle est la longueur de chaque étape? | On a 12,8 km que l’on regroupe 4 km par heure (4 par groupe). Combien de groupes y aura-t-il? |
| Représentation |
La languette représente l’unité (1 km)  Image Un ensemble de réglettes est composé de douze longues réglettes et de huit petites
réglettes en forme de cube. Une flèche pointe vers quatre ensembles identiques de réglettes placés en
dessous. Chacun des quatre ensembles comporte trois réglettes longues et trois petites réglettes cubes.
Toutes les réglettes sont bleues.
|
La languette représente l’unité (1 km)  Image Un ensemble de réglettes est composé de douze longues réglettes et de huit petites
réglettes en forme de cube. Une flèche pointe vers quatre ensembles de réglettes en dessous. Les trois
premiers ensembles contiennent quatre longues réglettes et le quatrième ensemble contient huit petites
réglettes cubes. Toutes les réglettes sont bleues.
Chaque groupe composé de 4 languettes représente une heure. Le dernier groupement représente huit quarantièmes (\(\frac{8}{{40}}\)) d’un groupe, ce qui est l’équivalent à deux dixièmes (\(\frac{2}{{10}}\) ou 0,2) d’heure. |
| Interprétation de la représentation | Le quotient représente le nombre d’éléments par groupe, soit 3,2 éléments par groupe. Chaque jour, les élèves devront donc parcourir 3,2 km. | Le quotient représente le nombre de groupes, soit 3,2 groupes. Il lui faudra donc 3,2 heures pour faire la randonnée. |
Dans une situation de partage, la compréhension du quotient est généralement assez simple puisque la partie décimale du quotient représente une partie ou une fraction d’un élément. Ainsi, dans le problème de partage précédent, il est assez clair que chaque groupe est composé de 3,2 km (3,2 éléments), soit 3 kilomètres entiers et 0,2 (\(\frac{2}{{10}}\)) d’un autre kilomètre.
Dans une situation de groupement, on compte des groupes. La partie décimale du quotient est alors plus complexe à interpréter puisque cette partie décimale représente une partie d’un groupe. Du problème de groupement précédent, les élèves peuvent comprendre le sens du quotient en effectuant une estimation à l’aide de nombres naturels. Ils peuvent alors affirmer que Pierre mettra un peu plus de 3 heures (\(3\; \times \;4\; = \;12\)) ou entre 3 et 4 heures pour faire la randonnée. Afin de déterminer un quotient en suivant le sens de groupement, il faut créer des groupes d’une grandeur donnée. Dans l’exemple, il s’agit de créer des groupes de 4 km. On crée 3 groupes et on se retrouve avec un autre groupe partiellement complet. Que représente cette partie d’un groupe? Dans une situation de groupement, c’est le groupe au complet qui devient l’unité qu’il faut compter. Ainsi, les 8 dixièmes d’une languette doivent être considérés comme fraction du groupe, le groupe étant composé de 4 languettes ou de 40 dixièmes de languette. Donc, les 0,8 dans ce groupe représentent alors 0,2 d’un groupe.
Le sens de partage reflète le sens le plus courant d’une division dont le dividende est un nombre décimal. De plus, comme mentionné précédemment, l’interprétation du quotient décimal est aussi plus accessible dans un contexte de partage. Il est tout de même important que les élèves soient exposés à quelques exemples de divisions qui revêtent le sens de groupement.
Tout comme avec la multiplication, les élèves peuvent découvrir, en utilisant une série d’opérations apparentées, que dans les divisions telles que \(72\; \div \;4\); \(\;7,2\; \div \;4\); \(\;0,72\; \div \;4\) et \(0,072\; \div \;4\) les chiffres qui composent les quotients sont les mêmes, dans le même ordre, et que seule la position de la virgule est différente.
Exemple
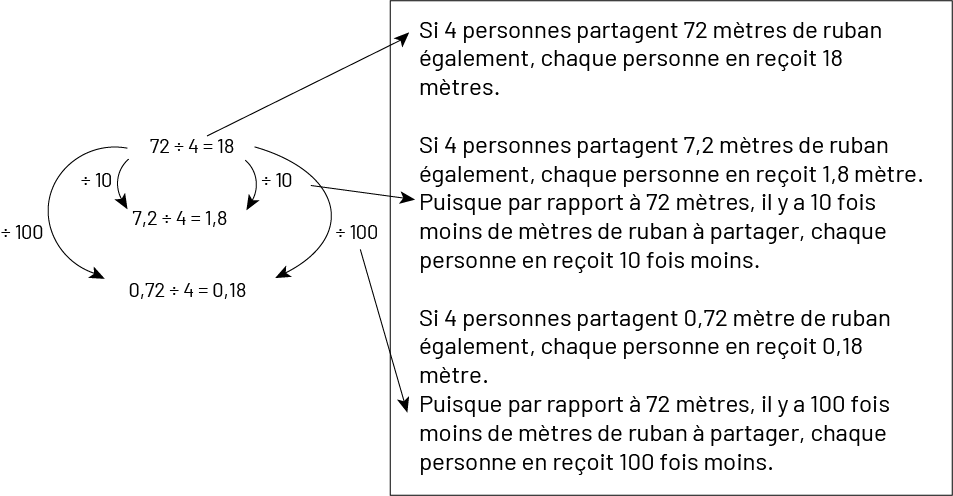
Image Trois divisions sont placées l'une sous l'autre, et à côté d'elles, un rectangle contient des explications textuelles.Première division : 72 divisé par quatre égale 18. Explication : Si quatre personnes partagent 72 mètres de ruban également, chaque personne en reçoit 18 mètres.Une flèche relie 72 au dividende de la deuxième division, et une flèche relie 18 au quotient de la deuxième division; toutes deux indiquent « divisé par dix ».Aussi, une flèche relie 72 au dividende de la troisième division, et une flèche relie 18 au quotient de la troisième division; toutes deux indiquent « divisé par cent ».Deuxième division : sept virgule deux divisé par quatre égale un virgule huit. Explication : Si quatre personnes partagent sept virgule deux mètres de ruban également, chaque personne en reçoit un virgule huit mètre. Puisque par rapport à 72 mètres, il y a dix fois moins de mètres que de ruban à partager, chaque personne en reçoit dix fois moins.Troisième division : zéro virgule 72 divisé par quatre égale zéro virgule 18. Explication : Si quatre personnes partagent zéro virgule 72 mètre de ruban également, chaque personne en reçoit zéro virgule 18 mètre. Puisque par rapport à 72 mètres, il y a cent fois moins de mètres de ruban à partager, chaque personne en reçoit cent fois moins.
Les élèves ont déjà vu que pour effectuer une multiplication comme \(4\; \times \;12,8\), elles et ils peuvent estimer la réponse (par exemple, le produit sera près de 48, car \(4\; \times \;12\; = \;48\)), effectuer la multiplication comme s’il s’agissait de nombres naturels (\(4\; \times \;128\)) pour obtenir le produit 512, puis placer la virgule à l’endroit approprié (51,2), en utilisant l’estimation comme indicateur de l’ordre de grandeur. Elles et ils peuvent procéder de façon semblable pour effectuer des divisions.
Exemple 1
On cherche à effectuer \(32,4\; \div \;3\).
On sait que la réponse est près de 10, car \(30\; \div \;3\; = \;10\).
On effectue la division comme s’il s’agissait de nombres naturels (\(324\; \div \;3\)) pour obtenir le quotient 108.
Ensuite, on place la virgule à l’endroit approprié, soit 10,8, sachant que la réponse est près de 10.
Note : Puisque 32,4 est 10 fois plus petit que 324, le quotient de \(32,4\; \div \;3\) (10,8) est 10 fois plus petit que le quotient de \(324\; \div \;3\) (108).
Exemple 2
On cherche à effectuer \(0,388\; \div \;4\).
Pour estimer, on peut penser que l’on a environ 400 millièmes à diviser par 4, ce qui donne environ 100 millièmes (0,100).
On peut aussi penser que l’on a environ 40 centièmes à diviser par 4, ce qui donne environ 10 centièmes (0,10) ou même que l’on a environ 4 dixièmes à diviser par 4, ce qui donne environ 1 dixième (0,1).
On effectue la division \(388\; \div \;4\) pour obtenir 97. On place la virgule à l’endroit approprié, soit 0,097, car on sait que la réponse est près de 0,100 ou 0,10 ou 0,1.
Il est préférable de se tenir à des réponses comportant un maximum de trois décimales. Pour ce faire, on peut procéder à rebours afin de choisir des nombres appropriés.
Exemple 3
On pense à la situation suivante :
Pendant ses vacances, Valérie veut effectuer un trajet de 15,3 km en une semaine. Elle décide de parcourir la même distance chaque jour pendant 7 jours. Quelle distance parcourra-t-elle chaque jour?
Avec une calculatrice, on détermine que \(15,3\; \div \;7\; = \;2,185\;714\)… On décide qu’il est préférable de modifier les données du problème pour obtenir comme réponse 2,2. Pour connaître le dividende, il suffit de calculer \(7\; \times \;2,2\). On obtient 15,4. La situation est alors modifiée comme suit :
Pendant ses vacances, Valérie veut effectuer un trajet de 15,4 km en une semaine. Elle décide de parcourir la même distance chaque jour pendant 7 jours. Quelle distance parcourra-t-elle chaque jour?
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83-87.
Lorsque la division d’un nombre décimal par un nombre naturel est effectuée en utilisant diverses stratégies, il est important que les élèves interprètent correctement le résultat. Pour ce faire, ils doivent se référer à l’estimation faite au préalable afin de s’assurer de l’ordre de grandeur du quotient. Ils doivent aussi se référer à la situation-problème afin de s’assurer du sens à donner au quotient, à savoir que le résultat obtenu représente la taille des groupes ou qu’il représente le nombre de groupes. Les élèves doivent aussi comprendre et être en mesure d’expliquer la stratégie retenue pour effectuer l’opération.
Souvent, lorsque la division d’un nombre décimal représente le sens de groupement, l’opération n’est pas effectuée selon ce sens puisque représenter un raisonnement de groupement exige la création et l’interprétation d’une partie d’un groupe, ce qui rend la démarche plus difficile à saisir. La division est alors le plus souvent effectuée en suivant un raisonnement de partage. Voici différentes stratégies de division, selon le sens de partage, d’un nombre décimal par un nombre naturel, par exemple :
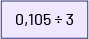
Afin d’estimer le quotient, il est possible de raisonner comme suit : 105 millièmes c’est près de 100 millièmes, et 100 millièmes \( \div \;3\), c’est un peu plus que 33 millièmes (0,033); donc 105 millièmes \( \div \;3\), c’est aussi un peu plus que 33 millièmes (0,033).
- Division à l’aide de matériel de base dix
Note : Le gros cube représente l’unité.
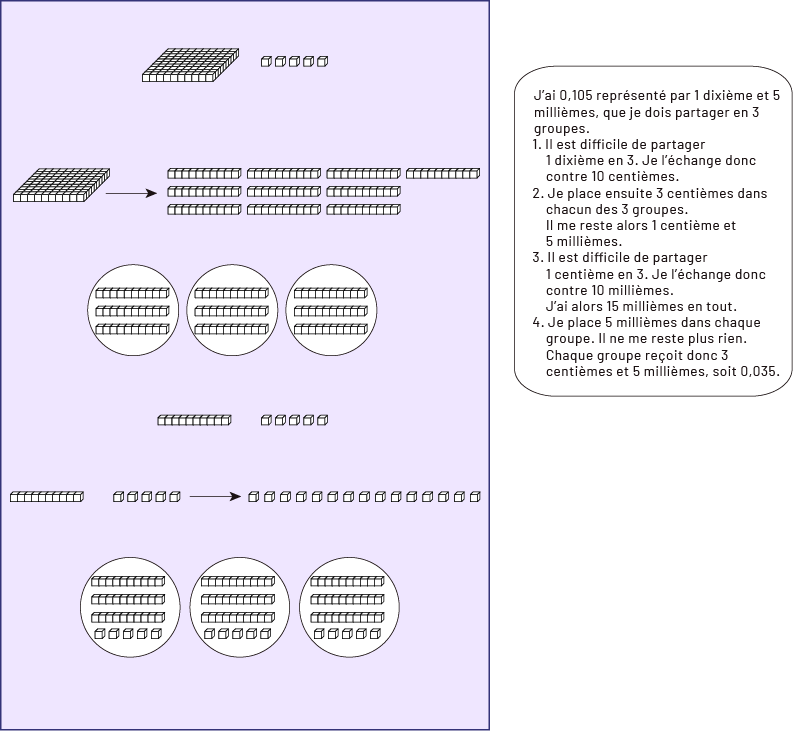
Image Dans un rectangle, le problème à résoudre est illustré par des réglettes. Un encadré à côté décompose textuellement le problème. L'encadré textuel dit : « J'ai zéro virgule 105 représenté par un dixième et cinq millièmes, que je dois partager en trois groupes. » L'illustration montre une grille de cent cubes unités, avec cinq cubes unités individuels à côté. L'encadré textuel dit : « Un : Il est difficile de partager un dixième en trois. Je l'échange donc contre dix centièmes. » L'illustration montre une grille de cent unités qui pointe à droite avec une flèche vers dix tours de dix unités. L'encadré textuel dit : « Deux : Je place ensuite trois centièmes dans chacun des trois groupes. Il me reste alors un centième et cinq millièmes. » L'illustration montre trois ensembles de trois tours de dix unités. En dessous, il y a une tour de dix unités et cinq cubes unités individuels. L'encadré textuel dit : « Trois : Il est difficile de partager un centième en trois. Je l'échange donc contre dix millièmes. J'ai alors 15 millièmes. » L'illustration montre une tour de dix unités, puis cinq unités individuelles qui pointent avec une flèche vers 15 unités individuelles. L'encadré textuel dit : « Quatre : Je place cinq millièmes dans chaque groupe. Il ne me reste plus rien. Chaque groupe reçoit donc trois centièmes et cinq millièmes, soit zéro virgule zéro trois cinq. » L'illustration montre trois ensembles de trois tours de dix unités et de cinq unités individuelles.
- Division à l’aide d’un algorithme personnel
Image Deux divisions écrites et résolues au long sont accompagnées d’un encadré textuel qui décrit le problème. Première division : zéro virgule 105 divisé par trois. Sous le dividende, il est écrit : moins zéro virgule 90 égale zéro virgule zéro quinze moins zéro virgule zéro quinze égale zéro. Sous le diviseur, il est écrit : zéro virgule zéro 30 plus zéro virgule zéro zéro cinq égale zéro virgule zéro 35. Deuxième division : trois divisé par zéro virgule 105. Première colonne : moins zéro virgule zéro 90 égale zéro virgule zéro 15 moins zéro virgule zéro quinze égale zéro. Deuxième colonne : zéro virgule zéro 30 plus zéro virgule zéro zéro cinq égale zéro virgule zéro 35. L’encadré textuel dit : Un : Il y a 105 millièmes. Je remets 30 millièmes à chaque groupe. J’enlève alors les 90 millièmes qui ont été distribués. Deux : Il me reste 15 millièmes. Je remets cinq autres millièmes à chaque groupe. J’enlève donc les 15 millièmes qui restaient. Trois : Chaque groupe est alors composé de 35 millièmes, soit zéro virgule zéro 35.
- Division à l’aide de l’algorithme usuel
Image Deux divisions écrites et résolues au long sont accompagnées d’un encadré textuel qui décrit le problème.Première division : zéro virgule zéro 35 est écrit au-dessus de trois divisé par zéro virgule 105 moins zéro virgule zéro neuf égale zéro virgule zéro 15 moins zéro virgule zéro 15 égale zéro.Deuxième division : zéro virgule 105 moins zéro virgule zéro neuf divisé par trois. Sous le dividende, il est écrit zéro virgule zéro 15 moins zéro virgule zéro 15 égale zéro; et sous le diviseur, il est écrit zéro virgule zéro 35. L’encadré textuel dit : J’ai 105 millièmes, ou zéro virgule 105, que je dois partager en trois groupes. Un : Je commence par examiner les unités. Il n’y en a pas, donc, j’inscris zéro et une virgule afin d’indiquer que dans le quotient il n’y aura pas d’unités. J’examine alors le chiffre dans la position des dixièmes. J’ai un dixième. Deux : N’ayant qu’un dixième, je ne peux placer un dixième dans chacun des trois groupes. Donc, j’inscris zéro pour indiquer qu’il n’y aura pas de dixièmes dans le quotient. Cependant, je remarque qu’un dixième, c’est équivalent à dix centièmes. Trois : Je cherche alors à partager dix centièmes en trois groupes. J’enlève neuf centièmes, ou trois fois trois centièmes, puisque je place trois centièmes dans chaque groupe. J’inscris trois dans la position des centièmes dans le quotient. Quatre : Il me reste un centième. Je ne peux pas placer un centième dans chacun des trois groupes. Toutefois, je constate qu’un centième, c’est équivalent à dix millièmes. Ces dix millièmes combinés aux cinq millièmes donnent 15 millièmes en tout. Cinq : Je partage alors les 15 millièmes en trois groupes, ou trois fois cinq millièmes. J’enlève donc 15 millièmes. J’inscris cinq dans la position des millièmes dans le quotient. Il ne me reste plus rien. Le quotient est donc zéro virgule zéro 35.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 107-110.
Connaissance : nombre décimal
Un nombre décimal est un nombre qui peut être exprimé en notation décimale avec une partie décimale finie.
Exemple
3,72 et 12,135
L’ensemble des nombres décimaux inclut tous les entiers, car ces derniers peuvent être exprimés avec une partie décimale.
Exemple
\(3\; = \;3,0\)
Il inclut aussi certaines fractions, comme \(\frac{2}{5}\) et \(\frac{3}{{16}}\), puisque \(\frac{2}{5}\; = \;0,4\) et \(\frac{3}{{16}}\; = \;0,1875\). On remarque alors que \(\frac{1}{2}\), \(\frac{5}{{10}}\) et 0,5 sont des représentations symboliques du même nombre décimal.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
Connaissance : rôle de la virgule
La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.
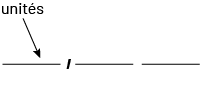
La position des unités définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, les centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.
Image
Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le
mot « unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les millièmes représentent une quantité mille fois plus petite que l’unité.
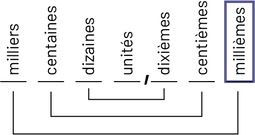Image Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. Le mot « millièmes » est encadré. Les mots « milliers » et « millièmes » sont réunis par un
trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Source : Guide d’enseignement efficace des mathématiques de la 4e à la
6e année, p. 51.
Connaissance: algorithme
Les algorithmes sont des ensembles de règles et d’actions ordonnées nécessaires à la résolution d’une addition, d’une soustraction, d’une multiplication ou d’une division. En termes simples, un algorithme est la « recette » d’une opération. (Kilpatrick, Swafford et Findell, 2001, p. 103)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 75.
Connaissance : algorithme usuel
Méthode standardisée pour effectuer une opération.
Exemple
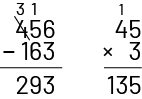Image
Deux opérations sont présentées verticalement, côte à côte. Une soustraction : 456 moins 163 égale 293. Un « un » est
retenu en haut de la colonne des dizaines. Le quatre de 456 est barré et un trois trône au-dessus. Une multiplication
: 45 fois trois égale 135. Un « un » est retenu au-dessus des dizaines.
Connaissance : algorithme personnel
Stratégie, généralement développée par l’élève, pour effectuer une opération.
Exemple
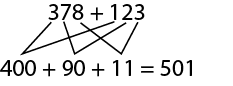Image
Deux additions sont écrites l’une au-dessus de l’autre. Première addition : 378 plus 123. Deuxième addition : 400 plus
90 plus 11 égale 591. 378 se relie à 400, 90 et 11, et chacun d’eux se relient à 123.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 76.