B2.11 Represent and solve problems involving the division of decimal numbers up to thousandths by whole numbers up to 10, using appropriate tools and strategies.
Representing and Solving Problems Involving the Division of Decimal Numbers up to Thousandths by Whole Numbers Up to 10
By Grade 6, students have learned that a division like \(12\; \div \;3\) is carried out according to a context where one either creates groups of 3 elements (grouping) or creates 3 equal groups (sharing). These two contexts also apply with a division of a decimal number by a whole number.
With understanding of these two meanings of division, students should recognize that the situation of dividing $23.50 equally among 5 friends has a sharing meaning and can be represented by \(23.50\; \div \;5\), where the quotient represents the size of a group (number of dollars a friend receives). They may also recognize that the situation of pouring 23.50 litres of juice into 5-litre containers has a grouping meaning and can also be represented by \(23.50\; \div \;5\). However, in this case, the quotient represents the number of groups (number of filled containers).
Regardless of the given situation (sharing or grouping), students should be able to estimate that the quotient is about 5 and they can use a strategy to determine that the quotient is equal to $4.70 (sharing) or 4.7 filled jugs (grouping).
The fractional nature of a decimal number makes the interpretation of quantities in a division more difficult than with whole numbers as shown in the following table.
| Empty Cell | Sharing | Grouping |
|---|---|---|
| Meaning of Quotient | We look for the number of elements in each group. | We are looking for the number of groups. |
| Problem | Students commit to walking 12.8 km in 4 days. How many kilometres do they have to walk each day if they want to cover the same distance each day? | Peter wants to hike 12.8 km at 4 km per hour. How many hours will it take him to complete this hike? |
| Operation | \(12.8 \div \;4\) | \(12.8 \div \;4\) |
| Questions to Ask | We divide the 12.8 km into 4 stages of equal length (4 groups). What is the length of each stage? | We have 12.8 km that we group into 4 km for each hour (4 per group). How many hours will there be? |
| Representation |
The rod represents the unit (1 km)  |
The rod represents the unit (1 km) 
Each group of 4 rods represents one hour. The last grouping represents eight fortieths \(\frac{8}{{40}}\) of a group, which is equivalent to two tenths \(\frac{2}{10}\) or one fifth \(\frac{1}{5}\) of an hour. |
| Interpreting the Representation | The quotient represents the number of elements per group, or 3.2 elements per group. Each day, the pupils will therefore have to cover 3.2 km. | The quotient represents the number of groups, which is 3.2 groups. It will therefore take him 3.2 hours to complete the hike. |
In a sharing situation, understanding the quotient is usually quite simple since the decimal part of the quotient represents a part or fraction of an element. Thus, in the previous sharing problem, it is fairly clear that each group is composed of 3.2 km (3.2 elements), which is 3 whole kilometres and 0.2 \(\frac{2}{10}\) of another kilometre.
In a grouping situation, we count groups. The decimal part of the quotient is more complex to interpret because it represents a part of a group. From the grouping problem above, students can understand the meaning of the quotient by making an estimate using whole numbers. They can reasonably determine that it will take Peter just over 3 hours (\(3 \times 4 = 12\)), or between 3 and 4 hours to complete the hike. In order to determine a quotient by grouping, we must create groups of a given size. In the example, groups of 4 km are created. It turns out that 3 groups can be created with another partially complete group. What does this partial group represent? In a grouping situation, the whole group (in this case 4 km) is the unit to be counted. Thus, the 8 tenths that is left over should be considered a fraction of a group of 4 km. Given that each group is equal to 4 km and each km has ten tenths, then the group composed of 4 rods is equal to 40 tenths. So the 0.8 in the remainder group can be parsed out as 0.2 to each group.
As mentioned previously, the interpretation of the decimal quotient is easier to interpret in a sharing context. For this reason, it is important that students have experience with division problems that involve grouping.
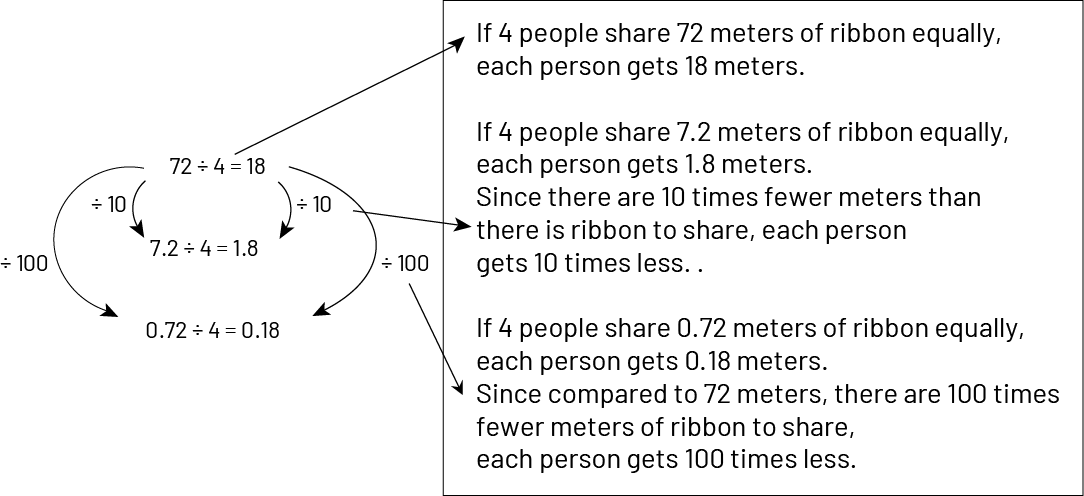
As with multiplication, students can discover, using a series of related operations, that in divisions such as \(72\; \div \;4\); \(\;7.2\; \div \;4\); \(\;0.72\; \div \;4\) and \(0.072\; \div \;4\) the digits that make up the quotients are the same, in the same order, and that only the position of the decimal point is different.
Example
Students have already seen that to perform a multiplication such as 4 x 12.8, they can estimate the answer. For example, the product will be close to 48, because 4 x 12 = 48. If the multiplication was done as if with whole numbers (4, 12) to get the product 512, and then place the decimal point in the middle 48, multiply as if they were whole numbers (\(4\; \times \;128\)) by multiplying the decimal by 10, then the product would be 512. The decimal point then needs to be replaced by dividing by 10 to compensate (51.2).
Example 1
\(32.4\; \div \;3\).
We know that the answer is close to 10, because \(30\; \div \;3\; = \;10\).
We can divide as if we had whole numbers \(324\; \div 3\) to get the quotient 108.
Then we place the decimal point in the appropriate place, knowing that the answer is close to 10.
Note: Since 32.4 is 10 times smaller than 324, the quotient of \(32.4\; \div \;3\) (10.8) is 10 times smaller than the quotient of \(324\; \div \;3\) (108).
Example 2:
\(0.388 \div \;4\).
To estimate, we can think that we have about 400 thousandths to divide by 4, which gives about 100 thousandths (0.100).
We can also think that we have about 40 hundredths to divide by 4, which gives about 10 hundredths (0.10) or even that we have about 4 tenths to divide by 4, which gives about 1 tenth (0.1).
We divide \(388\; \div \;4\) and get 97. We place the comma in the appropriate place, i.e. 0.097, because we know that the answer is close to 0.100 or 0.10 or 0.1.
It is best to stick to answers with a maximum of three decimal places. This can be done by working backwards to select appropriate numbers.
Example 3
Present the following situation:
During her vacation, Valerie wants to travel 15.3 km in one week. She decides to travel the same distance every day for 7 days. How far will she travel each day?
Using a calculator, we determine that \(15.3 \div \;7 = \;2.185\;714\). to round the answer to 2.2. To find the dividend by calculating \(7\; \times \;2.2\), we get 15.4. So Valerie will travel a little less than 2.2 km per day.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 83-87.
When dividing a decimal by a whole number using various strategies, it is important that students interpret the result correctly. To do so, they must refer to the estimate made beforehand to ensure that the magnitude of the quotient is reasonable. They must also refer to the problem situation to ensure that the quotient is meaningful, and represents a plausible size or number of groups. Students must also understand and be able to explain the strategy used to perform the operation.
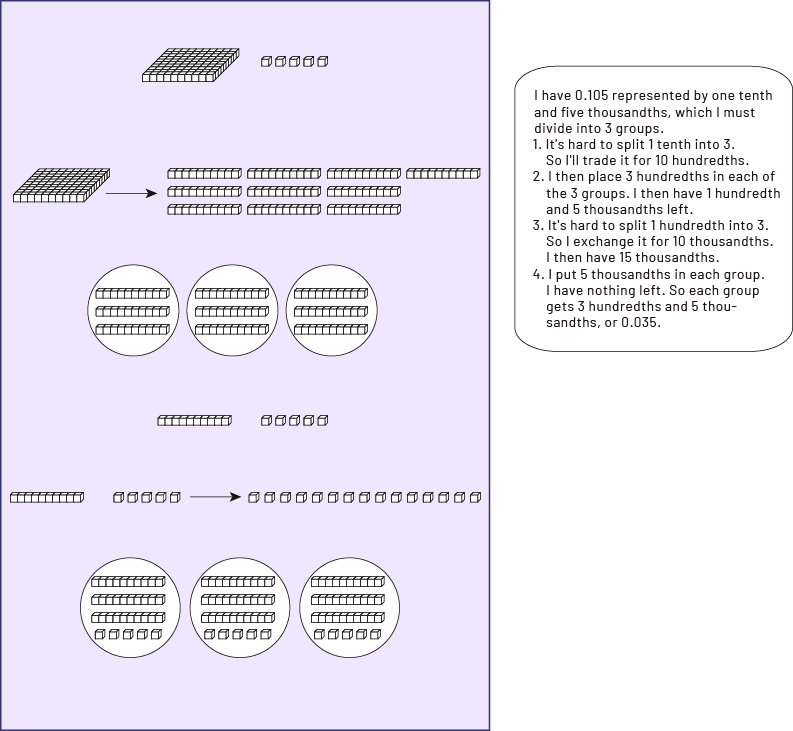
In order to estimate the quotient, it is possible to reason as follows: 105 thousandths is almost 100 thousandths, and 100 thousandths \( \div \;3\), it is a little more than 33 thousandths (0.033); so 105 thousandths \( \div \;3\) is also a bit more than 33 thousandths (0.033).
- Division using base ten blocks
Note: The large cube represents the whole.
- Division using student-generated algorithm

- Division using the standard algorithm

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 107-110.
Knowledge: Decimal Number
A decimal number is a number that has a decimal point, such as 3.75. The part before the decimal point represents a whole number amount, and the part after the decimal point represents a value that is less than one.
Example
3.72 and 12.135 64
All whole numbers can be expressed as decimals.
Example
\(3\; = \;3.0\)
Some fractions can also be expressed as decimals, such as \(\frac{2}{5}\), which is equal to \(\;0.4\) and \(\frac{3}{16}\), which is equal to 0.1875. We notice then that \(\frac{1}{2}\), \(\frac{5}{10}\) and 0,5 are symbolic representations of the same decimal number.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 28.
Knowledge: Role of the Decimal Point
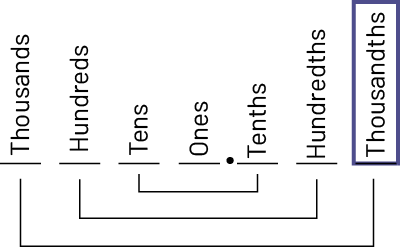
The decimal point plays a significant role in decimal notation. It separates the whole part from the decimal part.

The position of the ones defines the whole according to which are formed on the one hand the tenths, the hundredths and the thousandths and on the other hand the tens, the hundreds and the thousands. It can therefore be said that the ones, identified by the decimal point, is at the heart of the decimal system.

This recognition of the role of the ones digit is evidenced by the name prefixes given to the place value of the digits on either side of it. Thus, tenths represent a quantity ten times smaller than one and tens are ten times bigger.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 51.
Knowledge: Algorithm
Algorithms are sets of rules and ordered actions needed to solve an addition, subtraction, multiplication or division. In simple terms, an algorithm is the "recipe" for an operation. (Kilpatrick, Swafford and Findell, 2001, p. 103)
Knowledge: Standard Algorithm
Standardized method for performing an operation.
Example
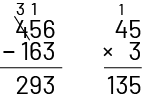
Knowledge: Student-Generated Algorithm
A strategy for solving a problem or performing a calculation, usually developed by a student.
Example
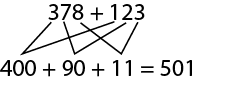
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 76.
