À vue d'oeil...

B2.12 Résoudre des problèmes comprenant des rapports, y compris des pourcentages et des taux, à l’aide d’outils et de stratégies appropriés.

Habileté : résoudre des problèmes comprenant des rapports, y compris des pourcentages et des taux, à l’aide d’outils et de stratégies appropriés

---

Le raisonnement multiplicatif est un concept qui exige la capacité de traiter plusieurs idées ou quantités à la fois. L’idée est de voir les problèmes selon des valeurs relatives plutôt qu’absolues. Examinons le problème suivant : « Si le poids d’un chien passe de 5 kg à 8 kg et que celui d’un autre chien passe de 3 kg à 6 kg, quel est le chien qui a le plus engraissé? » Si l’élève aborde le problème du point de vue des valeurs absolues ou des additions, elle ou il peut avoir tendance à répondre que les deux chiens ont pris autant de poids. Cependant, en se basant sur les valeurs relatives, l’élève peut affirmer que le deuxième chien a plus engraissé puisqu’il a doublé son poids de départ contrairement au premier, qui aurait dû atteindre 10 kg pour que sa prise de poids relative soit équivalente. Le tableau suivant illustre de manière visuelle les deux réponses de ce problème. S’il est vrai que les deux réponses peuvent se défendre, c’est sur la valeur relative (raisonnement multiplicatif) qu’il faut se baser pour appliquer un raisonnement proportionnel.

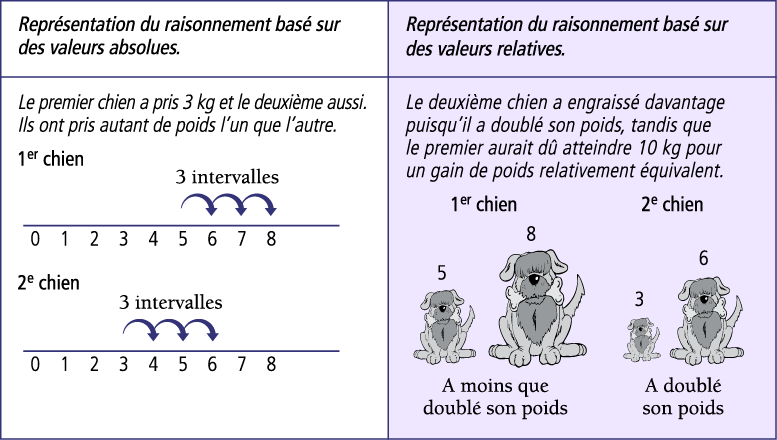
Image Un tableau est divisé en deux. Première partie : « Représentation du raisonnement basé sur des valeurs absolues. » « Le premier chien a pris trois kilos et le deuxième aussi. Ils ont pris autant de poids l’un que l'autre. » Associée au premier chien, la droite numérique est graduée de zéro à huit. Trois flèches relient respectivement cinq à six, six à sept et sept à huit en indiquant « trois intervalles ». Associée au deuxième chien, la droite numérique est graduée de zéro à huit. Trois flèches relient respectivement trois à quatre, quatre à cinq et cinq à six en indiquant « trois intervalles ». Deuxième partie : « Représentation du raisonnement basé sur des valeurs relatives. » « Le deuxième chien a engraissé davantage puisqu’il a doublé son poids, tandis que le premier aurait dû atteindre dix kilos pour un gain de poids relativement équivalent. » Pour le premier chien, il y a l’image d’un chien moyen, qui indique cinq, et d’un gros chien, qui indique huit. Il est écrit « A moins que doublé son poids ». Pour le deuxième chien, il y a l’image d’un petit chien, qui indique trois, et d’un moyen-gros chien, qui indique six. Il est écrit « A doublé son poids ».

Pourquoi est-ce important?

Il est difficile d’amener l’élève à passer d’un raisonnement additif à un raisonnement multiplicatif, d’où l’importance de débuter à un jeune âge. C’est la base même du programme-cadre de mathématiques de l’Ontario, de la 1^re à la 8^e année, qui comprend des idées importantes reliées entre elles comme la multiplication, la division, les fractions, les décimales, les rapports, les pourcentages et les fonctions linéaires. Il faut du temps, diverses situations d’apprentissage et toutes sortes d’occasions pour acquérir des connaissances de différentes façons.

Source : Qu’est-ce que le raisonnement proportionnel?, p. 5-6.

Un rapport est une comparaison entre deux quantités de la même unité.

Un taux, tout comme un rapport, est aussi une comparaison entre deux quantités, mais de différentes unités.

Les rapports sont présents dans le quotidien et dans plusieurs situations mathématiques, notamment dans les valeurs de position (par exemple, le rapport entre les unités et les unités de mille est de 1 000 : 1), dans les fractions (par exemple, \(\frac{2}{3}\) ou 2 : 3), dans les figures semblables (par exemple, un agrandissement de 1 : 3), dans les nombres décimaux (par exemple, le rapport entre les centièmes et les dixièmes est de 10 : 1), dans les unités de mesure du système métrique (par exemple, le rapport entre les mètres et les millimètres est de 1 : 1 000).

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 54.

Taux

Exemple 1

J’achète 2 sacs de riz pour 10 $.

Je peux représenter ce taux de différentes façons :

• Par des mots : 2 sacs de riz coûtent 10 $.
• Par une division : 2 sacs de riz / 10 $.
• Comme une fraction : \(\frac{{2\;\;{\rm{sacs\;\; de\;\; riz}}}}{10\;\$} \).

À l’aide de la relation multiplicative, je peux déterminer le taux d’autres quantités de riz, c’est-à-dire des taux équivalents.

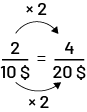
Pour 4 sacs de riz, le coût sera 20 $. 4 sacs c’est 2 fois plus que 2, donc le prix est 2 fois plus que 10 $.

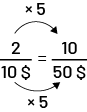
Pour 10 sacs de riz, le coût sera de 50 $. 10 sacs c’est 5 fois plus que 2, donc le prix est 5 fois plus que 10 $.

Je peux également déterminer le taux unitaire, soit le coût pour 1 sac de riz, à l’aide de la division.

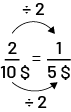
Pour 1 sac de riz, le coût sera 5 $. 1 sac c’est 2 fois moins que 2, donc le prix est 2 fois moins que 10 $. Le taux unitaire est donc 5 $/1 sac de riz.

On peut représenter les taux équivalents dans une table de valeurs en mettant l’accent sur la relation multiplicative et non additive.

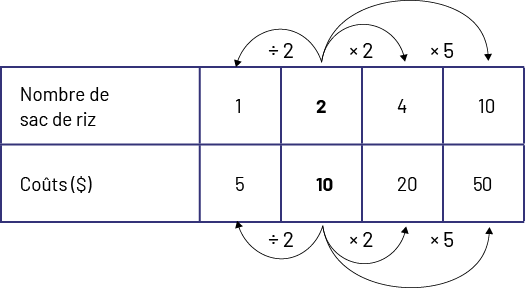
Image Un tableau indique dans une rangée le nombre de sacs de riz, et dans une autre rangée, les coûts en dollars. Nombre de sacs de riz : un, deux, quatre, dix. Une flèche va de deux à un en indiquant divisé par deux. Une flèche va de deux à quatre en indiquant fois deux. Une flèche va de deux à dix en indiquant fois cinq.Coûts en dollars : cinq, dix, vingt, cinquante. Une flèche va de dix à cinq en indiquant divisé par deux. Une flèche va de dix à vingt en indiquant fois deux. Et une flèche va de dix à cinquante en indiquant fois cinq.Les taux font partie de notre quotidien. On peut apporter les élèves à trouver différents exemples en lien avec les mesures (par exemple, je cours 12 km par heure, le vélo électrique roule à 35 km/heure, etc.) et les coûts (par exemple, 3 $ pour 12 pommes, 15 $/heure, etc.).Les élèves peuvent résoudre des problèmes en représentant des relations multiplicatives comprenant des taux en utilisant des contextes familiers.

Exemple 2

Si tu reçois 24 $ pour 2 heures de travail, combien d’argent obtiens-tu pour 4 heures? L’élève doit donc observer que 4 heures c’est le double ou deux fois plus que 2 heures donc le montant d’argent va également doubler, donc 48 $. Si on divise par 2, on peut trouver le taux unitaire, soit le montant d’argent reçu pour 1 heure de travail (12 $/heure).

On peut représenter ces relations dans une table de valeurs en mettant l’accent sur la relation multiplicative et non additive.

Dans cette table de valeurs, on peut également reconnaître qu’il existe une relation de proportionnalité entre le nombre d’heures travaillées et le montant d’argent reçu, soit × 12. Le coefficient de proportionnalité est de 12. On multiplie le nombre d’heures travaillées par 12 pour obtenir le montant d’argent reçu.

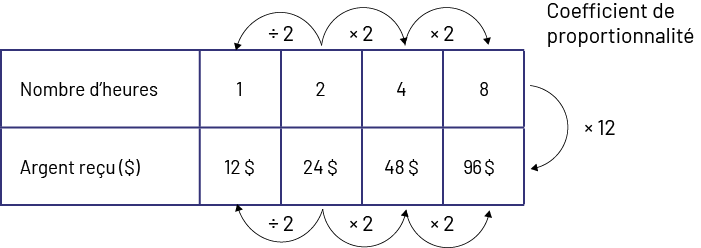
Image Un tableau indique dans une rangée le nombre d’heures, et dans une autre rangée, l’argent reçu en dollars. Nombre d’heures : un, deux, quatre, huit. Une flèche va de deux à un en indiquant divisé par deux. Une flèche va de deux à quatre en indiquant fois deux. Une flèche va de quatre à huit en indiquant fois deux. Argent reçu : douze dollars, 24 dollars, 48 dollars, 96 dollars. Une flèche va de 24 à douze en indiquant divisé par deux. Une flèche va de 24 à 48 en indiquant fois deux. Une flèche va de 48 à 96 en indiquant fois deux. Et une flèche va de la première à la deuxième rangée en indiquant fois douze. À droite du tableau il est écrit : Coefficient de proportionnalité. Un tableau de rapports peut aussi être construit sans que les valeurs soient inscrites dans un ordre croissant ou sans que toutes les valeurs soient inscrites. Il est en effet parfois plus facile de trouver la solution au problème en utilisant la relation de proportionnalité comme le démontre l’exemple suivant.

Exemple 3

La vidéo montre l’utilisation d’un tableau de rapports pour déterminer des taux équivalents.

Exemple 4

Abdala achète des viandes froides en vue de faire des sandwichs pour le pique-nique de l’école. Chaque kilogramme de viande coûte 12 $ et permet de préparer 10 sandwichs. Quel sera le coût de la viande nécessaire à la préparation 25 sandwichs?

Voici deux façons différentes d’utiliser la relation de proportionnalité dans un tableau de rapports pour résoudre ce problème.

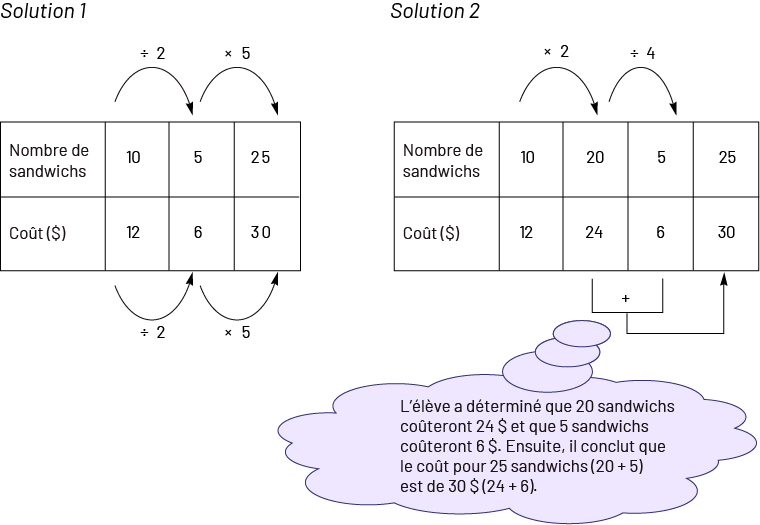
Image Solution un. Le tableau indique dans une rangée le nombre de sandwichs, et dans une autre rangée, le coût en dollars. Nombre de sandwichs : dix, cinq, 25. Une flèche va de dix à cinq en indiquant divisé par deux, et une flèche va de cinq à 25 en indiquant fois cinq. Cout : douze, six, trente. Une flèche va de douze à six en indiquant divisé par deux, et une flèche va de six à trente en indiquant fois cinq. Solution deux. Le tableau porte également sur le nombre de sandwichs et le coût en dollars. Nombre de sandwichs : dix, vingt, cinq, 25. Une flèche va de dix à vingt en indiquant fois deux. Une flèche va de vingt à cinq en indiquant divisé par quatre. Coût : douze, 24, six, trente. 24 s’unit à huit avec le symbole plus, qui lui se lie à trente avec une flèche. Ce dernier émet un phylactère de pensée qui dit : L’élève a déterminé que vingt sandwichs coûteront 24 dollars et que cinq sandwichs coûteront six dollars. Ensuite, il conclut que le coût pour 25 sandwichs, vinqt plus cinq, st de trente dollars, 24 plus huit.

Cette utilisation du tableau de rapports dans une situation de proportionnalité ne doit pas nécessairement être enseignée puisque les élèves, en situation de résolution de problèmes, peuvent la découvrir par eux-mêmes.

La droite numérique double met aussi en évidence des rapports qui permettent de résoudre un problème. Elle peut, par exemple, être employée à la place d'un tableau de rapports pour résoudre le problème précédent.

Image Une droite numérique indique zéro dollar et douze dollars, placés sur la première moitié de la droite. Au-dessus de zéro, il est écrit zéro sandwich, et au-dessus de douze, il est écrit dix sandwichs. Au-dessus de la droite, il y a un nuage dans lequel il est écrit : L’élève crée une droite numérique double et y situe les données du problème.

Les élèves situent ensuite sur la droite des rapports équivalent à celui donné dans le but de résoudre le problème. Les élèves peuvent choisir les rapports en fonction de leurs besoins et de leur compréhension du problème. Voici deux façons différentes de résoudre le problème à l’aide d’une droite numérique double.

Image Solution un. Une droite numérique indique zéro dollar, six dollars, douze dollars et trente dollars. Au-dessus de zéro il est écrit zéro sandwich, au-dessus de six il est écrit cinq sandwichs, au-dessus de douze il est écrit dix sandwichs et au-dessus de 30 il est écrit 25 sandwichs. Au-dessus de la droite, il y a un nuage dans lequel il est écrit : L’élève situe sur la droite la moitié des quantités données, soit cinq sandwichs à six dollars, puis détermine que 25 sandwichs, cinq fois cinq sandwichs, correspondent à 30 dollars, cinq fois six dollars. Solution deux. Une droite numérique indique zéro dollar, six dollars, douze dollars, 24 dollars et 30 dollars. Au-dessus de zéro il est écrit zéro sandwich, au-dessus de six il est écrit cinq sandwichs, au-dessus de douze il est écrit dix sandwichs, au-dessus de 24 il est écrit vingt sandwichs, et au-dessus de 30 il est écrit 25 sandwichs. Au-dessus de la droite, il y a un nuage dans lequel il est écrit : L’élève situe sur la droite le double des quantités données, soit vingt sandwichs pour 24 dollars, puis la moitié des quantités données, soit cinq sandwichs pour six dollars. Il ou elle situe ensuite 25 sandwichs, cinq sandwichs plus vingt sandwichs, pour trente dollars, six dollars plus 24 dollars.

La différence entre l’utilisation d'un tableau de rapports et de la droite numérique double pour représenter une situation de proportionnalité réside dans l’ordre dans lequel sont placées les valeurs qui représentent des rapports. Sur une droite numérique double, les nombres sont placés en ordre croissant en suivant des intervalles constants, alors que dans le tableau de rapports, ils sont placés selon l’ordre qui répond au raisonnement suivi pour résoudre la situation.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 52-53.

Pourcentage

En 6^e année, puisque les élèves sont exposés au concept de rapport, elles et ils apprennent qu’un pourcentage représente un rapport à 100 (par exemple, 30 % représente le rapport 30 : 100).

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 35.

Tout rapport peut être exprimé en pourcentage et dès qu’un résultat est exprimé en pourcentage, il peut être réécrit sous forme de fraction décimale et être ensuite représenté par une fraction équivalente.

Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Il est important de souligner qu’un résultat exprimé en pourcentage ne signifie pas que la quantité en question est nécessairement composée de 100 parties, comme expliqué dans le tableau suivant.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 35.

Au cycle moyen, les proportions sont enseignées de façon formelle. Au début, il s’agit de mettre en valeur la connaissance et la compréhension qu’ont les élèves des fractions équivalentes. Les élèves qui ont assimilé le concept de fractions équivalentes peuvent utiliser les relations multiplicatives pour résoudre des problèmes comportant des proportions quand la réponse recherchée est un nombre naturel (par exemple, \(\frac{2}{{10}}\; = \;\frac{?}{{40}}\)).

Les relations de proportionnalité permettent de résoudre une multitude de problèmes tirés du quotidien en ayant recours à un raisonnement simple à la portée des élèves du cycle moyen. Par exemple, si 30 % des 500 élèves d’une école aiment le couscous, il est possible de déterminer, de diverses façons, qu’il y a 150 élèves qui aiment le couscous. Voici quelques exemples.

Exemple 1

Créer une représentation semi-concrète.

Exemple 2

Construire une table de valeurs.

Image Un tableau indique, dans sa première colonne, le nombre de personnes dans l’école, et dans sa deuxième colonne, le nombre de personnes aimant le couscous. Nombres de la première colonne : cent, 200, 300, 400, 500. Une flèche va de cent à 200 en indiquant fois deux. Une flèche va de cent à 300 en indiquant fois trois. Une flèche va de cent à 400 en indiquant fois quatre. Et une flèche va de cent à 500 en indiquant fois cinq. Nombres de la deuxième colonne : 30, 60, 90, 120, 150. Une flèche va de 30 à 60 en indiquant fois deux. Une flèche va de 30 à 90 en indiquant fois trois. Une flèche va de 30 à 120 en indiquant fois quatre. Et une flèche va de 30 à 150 en indiquant fois cinq.

Exemple 3

Déterminer des fractions équivalentes.

\(\frac{{30}}{{100}}\; = \;\frac{{60}}{{200}}\; = \;\frac{{90}}{{300}}\; = \;\frac{{120}}{{400}}\; = \;\frac{{150}}{{500}}\)

Exemple 4

Établir une proportion par multiplication.

\(\begin{array}{l}\frac{{30}}{{100}}\; = \;\frac{?}{{500}}\\\frac{{30\; \times \;5}}{{100\; \times \;5}}\; = \;\frac{{150}}{{500}}\end{array}\)

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 55-56.

Rapports

Il y a une relation de proportionnalité entre deux quantités lorsque ces quantités peuvent augmenter ou diminuer simultanément selon le même facteur.

Exemple 1

Pour permettre aux élèves de réaliser une activité, le personnel enseignant distribue des pailles comme suit :

• l’élève qui travaille seul reçoit 4 pailles;
• une équipe de 2 élèves reçoit 8 pailles;
• une équipe de 3 élèves reçoit 12 pailles.

Une étude de la régularité de cette relation permet de reconnaître que le nombre d’élèves et le nombre de pailles augmentent selon le même facteur (facteur de 2 pour 2 élèves, facteur de 3 pour 3 élèves). Il devient alors aisé de déterminer qu’un groupe de 6 élèves recevra 24 pailles (facteur de 6). La relation de proportionnalité entre le nombre d’élèves et le nombre de pailles peut être représentée par l’égalité entre deux des rapports (par exemple, \(\frac{1}{4}\; = \;\frac{3}{{12}}\)). Une telle égalité entre deux rapports s’appelle une proportion.

La situation suivante, en revanche, ne présente pas de relation de proportionnalité.

Exemple 2

Pour permettre aux élèves de réaliser une activité, le personnel enseignant distribue des pailles comme suit :

• 1 élève qui travaille seul reçoit 5 pailles;
• une équipe de 2 élèves reçoit 9 pailles;
• une équipe de 3 élèves reçoit 13 pailles.

Dans cette situation, il est impossible d’établir une égalité entre deux rapports (par exemple, \(\frac{1}{5}\; \ne \;\frac{3}{{13}}\)). L’analyse de relations de proportionnalité s’effectue en appliquant un raisonnement proportionnel. Ce raisonnement intervient lors de la comparaison de deux rapports entre eux et de la reconnaissance d’une relation multiplicative. À noter que les relations multiplicatives incluent l’opération de division, puisque toute division peut être transformée en multiplication (par exemple, diviser par 2 est l’équivalent de multiplier par \(\frac{1}{2}\)).

L’habileté à utiliser un raisonnement proportionnel se développe tout au long de l’apprentissage des mathématiques. Par exemple, le personnel enseignant demande aux élèves du cycle primaire de déterminer le nombre de morceaux que contiennent 3 tablettes de chocolat si une tablette contient 8 morceaux. Il s’agit d’une relation multiplicative puisque le nombre de morceaux est 8 fois plus grand que le nombre de tablettes (rapport de 8 à 1). Cependant, pour résoudre ce genre de problème, les élèves auront d’abord recours à l’addition répétée (\(8\; + \;8\; + \;8\)). Par la suite, lorsque les élèves auront été exposés au concept de multiplication, les élèves pourront le résoudre en multipliant (\(8\; \times \;3\)), ce qui constitue un premier pas vers l’utilisation d’un raisonnement proportionnel.

Les termes rapport et proportion, ainsi que les notations qui s’y rattachent (par exemple, 2 : 3), font partie du programme-cadre de mathématiques au cycle moyen. De plus, les élèves développent des stratégies pour résoudre algébriquement un problème impliquant une relation de proportionnalité. En 4^e année, l’étude des relations de proportionnalité porte plutôt sur la reconnaissance et sur la description de la relation multiplicative dans diverses situations de résolution de problèmes. Les élèves utilisent intuitivement le raisonnement proportionnel pour résoudre des problèmes impliquant deux quantités qui sont dans un rapport de un à plusieurs (par exemple, 1 tablette pour 8 morceaux), de plusieurs à un (par exemple, 3 personnes par table) ou de plusieurs à plusieurs (par exemple, 2 litres de jus pour 5 personnes). Ils utilisent aussi du matériel concret et divers modèles tels que des illustrations, des tables de valeurs ou des droites numériques.

Exemple 3

Pour la journée d’athlétisme, les élèves de la classe de Mme Guérin préparent du jus pour les coureurs. Pour chaque contenant de jus concentré, il faut ajouter 3 contenants d’eau. Combien leur faudra-t-il ajouter de contenants d’eau à 4 contenants de jus concentré?

Solution à l’aide d’illustrations

Image À gauche d’une ligne verticale, il y a une boîte violette pointant par en dessous à l’aide de trois flèches vers trois boîtes blanches. À droite de la ligne verticale, ce même schéma se répète quatre fois.

Il faudra donc 12 contenants d’eau (\(4\; \times \;3\) contenants d’eau).

Solution à l’aide d’un table de valeurs

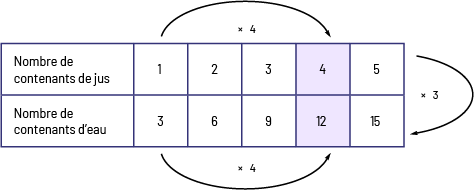
Image Un tableau horizontal possède deux rangées correspondant respectivement au nombre de contenants de jus et au nombre de contenants d’eau. Nombre de contenants de jus : un, deux, trois, quatre, cinq. Une flèche relie un à quatre en indiquant fois quatre. Nombre de contenants d’eau : trois, six, neuf, douze, quinze. Une flèche relie trois à douze en indiquant fois quatre. Les cases correspondant à quatre et à douze sont violettes tandis que les autres sont blanches. Une flèche relie la première rangée à la deuxième en indiquant fois trois.

Dans cette table de valeurs qui représente une situation de proportionnalité, les rapports entre les quantités correspondantes sont équivalents. Dans l’exemple précédent, on reconnaît aisément la relation multiplicative par 3 (coefficient de proportionnalité) entre le nombre de contenants de jus et le nombre de contenants d’eau. De plus, cette table de valeurs permet d’établir des proportions (par exemple, \(\frac{1}{3}\; = \;\frac{4}{{12}}\)).

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 49-51.

Connaissance : rapport

---

Les rapports permettent de comparer une partie à un tout, deux parties entre elles, ou deux quantités l’une avec l’autre. Un rapport s’écrit de façon symbolique avec un deux-points.

Exemple

Le rapport entre les billes bleues et les billes rouges est de 10 : 15 qui se dit « 10 à 15 ».

Une relation de rapports peut également être décrite au moyen de fractions, de nombres décimaux et de pourcentages.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Connaissance: pourcentage

---

Le pourcentage est une façon particulière de présenter une fraction. Il est souvent employé dans la vie courante. Une expression numérique comme 30 % (qui se lit « trente pour cent ») est en réalité une autre notation du nombre trente centièmes, soit \(\frac{{30}}{{100}}\) ou 0,30. Afin de faciliter la compréhension du concept de pourcentage, il faut d’abord amener les élèves à établir le lien entre le pourcentage et la fraction dont le dénominateur est 100, et ce, à l’aide de matériel concret ou semi-concret. Le pourcentage représente également un rapport de 1 : 100.

Exemple

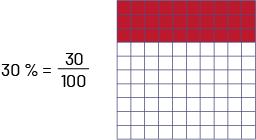
Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 34.

Connaissance : taux

---

Un taux décrit la relation multiplicative entre deux quantités exprimées avec des unités différentes (par exemple, bananes pour un dollar; barres de céréales par enfant; kilomètres par heure).

Un taux peut être exprimé en des mots tels que 150 kilomètres aux 3 heures.

Un taux peut être exprimé comme une division telle que 50 km/h.

Il existe de nombreuses applications des taux dans la vie quotidienne.

Remarque :

Comme pour les rapports, les taux font des comparaisons basées sur la multiplication et la division; cependant, les taux comparent deux mesures ou quantités liées, mais différentes. Par exemple, si 12 biscuits ont été mangés par 4 personnes, le taux serait de 12 biscuits par 4 personnes. Un taux équivalent serait de 6 biscuits par 2 personnes. Un taux unitaire serait de 3 biscuits par personne.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Connaissance : taux unitaire

---

Taux dont le deuxième terme du rapport est 1 (par exemple, coût de 0,35 $/mg).

Source : En avant, les maths! 6^e année, CM, Nombres, p. 2.