B2.12 Solve problems involving ratios, including percents and rates, using appropriate tools and strategies.
Skill: Solving Problems Involving Ratios, Including Percents and Rates, Using Appropriate Tools and Strategies
Multiplicative reasoning is a concept that requires the ability to deal with several ideas or quantities at once. The idea is to see problems in relative rather than absolute values. Consider the following problem, "If one dog's weight goes from 5 kg to 8 kg and another dog's weight goes from 3 kg to 6 kg, which dog gained more weight?" If the student is approaching the problem from the perspective of absolute values or addition, they may be inclined to answer that the two dogs have gained equal weight. However, based on relative values, the student may argue that the second dog gained more weight since it doubled its starting weight as opposed to the first dog, which would have had to reach 10 kg for its relative weight gain to be equivalent. The following table visually illustrates the two answers to this problem. If it is true that the two answers can be defended, it is on the relative value (multiplicative reasoning) that proportional reasoning is based.

Source: Paying attention to proportional reasoning, 2012, Ontario Ministry of Education, p. 4.
Why is this important?
Helping students bridge from additive to multiplicative thinking is complex but starts early. It forms the backbone of the Mathematics Curriculum and includes important and interconnected ideas such as multiplication, division, fractions, decimals, ratios, percentages and linear functions. It requires time, a variety of situations and opportunities to construct their understanding in multiple ways.
Source: Paying attention to proportional reasoning, 2012, Ontario Ministry of Education, p. 5-6.
A ratio is a comparison between two quantities of the same unit.
A rate, like a ratio, is also a comparison between two quantities, but of different units.
Ratios are present in everyday life and in many mathematical situations, including in place values (for example, the ratio of units to thousandths is 1 000:1), in fractions (such as \(\frac{2}{3}\) or \(2 \div 3\)), in similar figures (for example an enlargement of \(1 \div 3\)), in decimal numbers (for example the ratio of hundredths to tenths is 10:1), in metric units of measure (for example the ratio of metres to millimeters is 1:1000).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 54.
Rates
Example 1
I buy 2 bags of rice for $10.
I can represent this rate in different ways:
- Using words: 2 bags of rice cost $10.
- By division: 2 bags of rice / $10.
- As a fraction: \(\frac{{2\;{\rm{bags\; of\; rice}}}}{\$10}\).
Using the multiplicative relationship, I can determine the rate of other quantities of rice, namely equivalent rates.
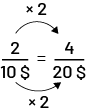
For 4 bags of rice, the cost will be $20. 4 bags is twice as much as 2, so the price is twice as much as $10.
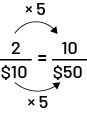
For 10 bags of rice, the cost will be $50. 10 bags is 5 times more than 2, so the price is 5 times more than $10.
I can also determine the unit rate, the cost per 1 bag of rice, using division.
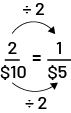
1 bag is half as much as 2 bags, so if the price of 2 bags is $10, then the price of 1 bag is half as much, or $5. So, the unit rate is $5/1 bag of rice.
Equivalent rates can be represented in a ratio table with emphasis on the multiplicative, not additive, relationship.
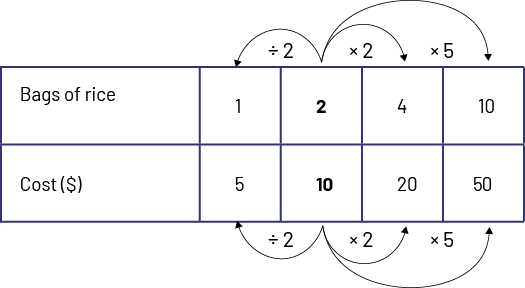
Rates are part of our daily lives. Students should be supported to find different examples related to measurements (for example, I run 12 km per hour, the electric bike goes 35 km per hour, etc.) and costs (for example, $3 for 12 apples, $15/hour, etc.).
Students can solve problems representing multiplicative relationships involving rates using familiar contexts.
Example 2
If you get $24 for 2 hours of work, how much money do you get for 4 hours? For a problem like this, students should notice that 4 hours is double or twice as much as 2 hours so the amount of money will also double, to $48. If we divide the rate by 2, we can find the unit rate, which is the amount of money received for 1 hour of work ($12/hour).
These relationships can be represented in a ratio table with an emphasis on the multiplicative, not additive, relationships.
In this ratio table, we can also recognize that there is a proportional relationship between the number of hours worked and the amount of money received, that is, × 12. We multiply the number of hours worked by 12 to get the amount of money received.
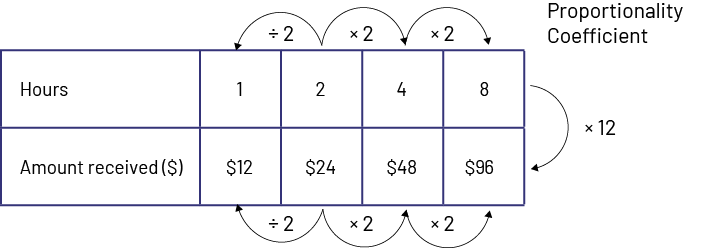
A ratio table can also be constructed without listing the values in ascending order or without listing all the values. It is sometimes easier to find the solution to the problem by using the proportionality relationship as shown in the following example.
Example 3
Abdala buys cold cuts to make sandwiches for the school picnic. Each kilogram of meat costs $12 and will make 10 sandwiches. How much will the meat cost to make 25 sandwiches?
Here are two different ways to use the proportionality relationship in a ratio table to solve this problem.

The use of a ratio table in a proportionality situation does not necessarily need explicit teaching. Students,
when faced with problem-solving situations, can intuitively recognize and apply it on their own.
The double number line also highlights relationships that can be used to solve a problem. It can, for example, be used instead of a ratio table to solve the previous problem.

Students then locate ratios on the right that are equivalent to the one given. Students can choose ratios based on their own knowledge and understanding of the problem. Here are two different ways to solve the problem using a double number line:

The difference between using a ratio table and the double number line to represent a proportionality situation is the order in which the values that represent ratios are placed. On a double number line, the numbers are placed in ascending order at constant intervals, whereas in the ratio table, they are placed in the order that corresponds to the reasoning used to solve the situation.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 52-53.
Percentage
In Grade 6, since students are exposed to the concept of ratio, they learn that a percentage represents a ratio of 100 (for example, 30% represents the ratio 30:100).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 35.
Any ratio can be expressed as a percent and once a result is expressed as a percent, it can be rewritten as a decimal fraction and then represented by an equivalent fraction.
Source: Adapted from Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
It is important to note that a result expressed as a percentage does not mean that the quantity in question is necessarily composed of 100 parts, as explained in the following table.
| Representation | Percentage | Instructional Notes |
|---|---|---|
  |
The ratio of green circles to the total number of circles is 3:4 or \(\frac{3}{4}\) and this can be interpreted as "75% of the circles are green." | Even if 75% of the circles are green, it does not mean that there are 100 circles in the whole. However, if there were 100 circles, there would be 75 green circles. Also, the fraction of circles that are green is equivalent to \(\frac{{75}}{{100}}\) (for example, \(\frac{3}{4}\; = \;\frac{75}{{100}}\) and if this number were doubled the corresponding fraction would be: \(\frac{{150}}{{200}}\; = \;\frac{75}{100}\). |
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 35.
In the junior grades, proportions are taught formally. Initially, the focus is on building students' knowledge and understanding of equivalent fractions. Students who have mastered the concept of equivalent fractions can use multiplicative relationships to solve problems involving proportions when the answer is a whole number (for example, \(\frac{{2}}{{10}}\) = \(\frac{?}{40}\)).
Proportional relationships can be used to solve a variety of everyday problems using simple reasoning that is accessible to junior students. For example, if 30% of the 500 students in a school like couscous, it is possible to determine in various ways that 150 students like couscous. Here are some examples.
Example 1
Use a visual representation.

Example 2:
Build a ratio table.

Example 3
Determine equivalent fractions.
\(\frac{{30}}{{100}} = \frac{60}{200} = \frac{90}{300} = \frac{120}{400} = \frac{150}{500}\)
Example 4
Establish a proportion by multiplication.
\(\begin{array}{l}\frac{{30}}{{100}}\; = \;\frac{?}{{500}}\\\frac{{30\; \times \;5}}{{100\; \times \;5}}\; = \;\frac{{150}}{{500}}\end{array}\)
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 55-56.
Ratios
There is a relationship of proportionality between two quantities when these quantities increase or decrease simultaneously by the same factor.
Example 1
To enable students to complete an activity, teachers distribute straws as follows:
- the student who works alone receives 4 straws;
- a team of 2 students receives 8 straws;
- a team of 3 students receives 12 straws.
A study of the pattern in this relationship allows us to recognize that the number of students and the number of straws increases proportionally (multiple of 4 for 2 students, multiple of 4 for 3 students). It then becomes easy to determine that a group of 6 students will receive 24 straws (multiple of 4). The proportional relationship between the number of students and the number of straws can be represented by the equality between the ratios (for example, "="). Such an equality between 2 ratios is called a proportion.
The following situation, on the other hand, does not have a proportional relationship.
Example 2
To enable students to complete an activity, teachers distribute straws as follows:
- 1 student working alone receives 5 straws;
- a team of 2 students receives 9 straws;
- a team of 3 students receives 13 straws.
In this situation, it is impossible to establish an equality between two ratios (for example \(\frac{1}{5}\; \ne \;\frac{3}{{13}}\)).
The analysis of proportional relationships is done by applying proportional reasoning. This reasoning is used when comparing two ratios and recognizing a multiplicative relationship. Note that multiplicative relations include the operation of division, since any division can be transformed into multiplication (for example, dividing by 2 is equivalent to multiplying by \(\frac{1}{2}\)).
The ability to use proportional reasoning develops throughout the learning of mathematics. For example, teachers ask primary students to determine the number of pieces in 3 chocolate bars if a bar contains 8 pieces. This is a multiplicative relationship since the number of pieces is 8 times greater than the number of bars (ratio of 8 to 1). However, to solve this kind of problem, students will first use repeated addition \(\left( {8\; + \;8\; + \;8} \right)\). Later, when they have been exposed to the concept of multiplication, they can solve it by multiplying \(\left( {8\; \times \;3} \right)\), which is a first step towards using proportional reasoning.
The terms ratio and proportion, and their related notations (for example, 2:3), are part of the junior mathematics curriculum. In addition, students will learn about and develop strategies for algebraically solving a problem involving proportionality. Beginning in Grade 4 , the study of proportional relationships focused on the recognizing and describing multiplicative relationship in a variety of problem-solving situations. Students intuitively use proportional reasoning to solve problems involving 2 quantities that are in a ratio of 1 to many (for example, 1 bar for 8 pieces), many to 1 (for example, 3 people per table) or many to many (for example, 2 litres of juice for 5 people). They also use concrete and visual (semi-concrete) models, ratio tables or number lines.
Example 3
For track and field day, students in Ms. Guerin's class prepare juice for the runners. For each container of juice concentrate, they need to add 3 containers of water. How many containers of water will they need to add to 4 containers of juice concentrate?
Solution Using Visuals

This will require 12 containers of water (\(4\; \times \;3\) containers of water).
Solution Using a Ratio Table

In a ratio table that represents a situation of proportionality, the factor that connects corresponding quantities is constant. In the example above, the multiplicative relationship "times 3" between the number of containers of juice and the number of containers of water is easily recognized. In addition, this ratio table allows us to establish proportions (for example, \(\frac{1}{3}\; = \;\frac{4}{{12}}\)) for different numbers of juice containers or water containers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 49-51.
Knowledge: Ratios
Ratios can compare one part to another part of the same whole, or a part to the whole. A ratio is written symbolically with a colon.
Example
The ratio of blue marbles to red marbles is 10:15 which reads "10 to 15".
A ratio relationship can also be described using fractions, decimal numbers and percentages.
Source: Adapted from Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Knowledge: Percent
A percent is a special kind of fraction with a denominator of 100. It is often used in everyday life. A numeric expression like 30% (which reads "thirty percent") is actually another notation for the number thirty hundredths, which can be represented as \(\frac{{30}}{{100}}\) or 0.30. To facilitate understanding of percent, students should first be introduced to the relationship between percents and fractions with a denominator of 100, using concrete or visual materials. The percentage also represents 1: 100.
Example
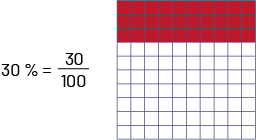
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 34.
Knowledge: Rate
A rate describes the multiplicative relationship between two quantities expressed with different units (eg, bananas per dollar; cereal bars per child; kilometres per hour).
A rate can be expressed in words such as 150 kilometres per 3 hours.
A rate can be expressed as a division such as 50 km/h.
There are many applications of rates in everyday life.
Note
Like ratios, rates make comparisons based on multiplication and division; however, rates compare two related, but different, measures or quantities. For example, if 12 cookies were eaten by 4 people, the rate would be 12 cookies per 4 people. An equivalent rate would be 6 cookies per 2 people. A unit rate would be 3 cookies per person.
Source: Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020..
Knowledge: Unit Rate
Rate where the second term of the ratio is 1 (for example, cost of $0.35/mg).
Source: translated from En avant, les maths! 6e, CM, Nombres, p. 2.
