La vue d'ensemble

À vue d'oeil...

Un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

B2.2 Comprendre les critères de divisibilité et les utiliser pour vérifier si les nombres sont divisibles par 2, 3, 4, 5, 6, 8, 9, et 10.

Habileté : comprendre et utiliser les critères de divisibilité

Relations multiplicatives et de divisibilité

Les relations multiplicatives et de divisibilité entre deux nombres sont des relations fondées respectivement sur la multiplication et sur la division. Par exemple, il y a une relation multiplicative entre 3 et 15 puisque 15 est un multiple de 3, et aussi une relation de divisibilité puisque 15 est divisible par 3.

À partir de la reconnaissance de ces relations, les élèves au cycle moyen peuvent identifier diverses caractéristiques d’un nombre naturel, notamment le fait que ce nombre peut être :

  • un nombre pair ou un nombre impair;
  • un facteur et un diviseur d’un autre nombre;
  • divisible par un autre nombre.

L’étude de ces caractéristiques des nombres naturels aide les élèves à développer le sens du nombre et à mieux utiliser les nombres dans des situations quotidiennes. Ces caractéristiques sont expliquées plus en détail dans ce qui suit à l’intention du personnel enseignant. Avec les élèves, il faut cependant éviter de s’attarder aux « trucs », à la terminologie et aux définitions. L’important pour les élèves est de développer une compréhension conceptuelle de ces caractéristiques à partir d’activités qui misent sur la reconnaissance des relations multiplicatives ou de divisibilité.

Nombre pair ou nombre impair

Si un nombre naturel est divisible en deux parties égales, c’est un nombre pair; sinon, c’est un nombre impair. La définition des nombres pairs et des nombres impairs est donc associée à la relation de divisibilité ou de non-divisibilité par 2.

C’est dans le cadre d’activités que les élèves devraient être amenés à constater que tous les nombres naturels ayant le chiffre 0, 2, 4, 6, ou 8 dans la position des unités sont des nombres pairs alors que ceux ayant le chiffre 1, 3, 5, 7 ou 9 dans la position des unités sont des nombres impairs. Ces constats leur permettent par la suite de reconnaître rapidement si un nombre est pair ou impair sans avoir à vérifier la divisibilité par 2.

Facteur et diviseur d’un nombre

Dans une multiplication de deux ou de plusieurs nombres naturels, chacun de ces nombres est appelé un facteur du nombre qui constitue le produit. Par exemple, 2 et 8 sont des facteurs de 16.

Dans l’équation deux fois huit égale 16, deux et huit sont les facteurs, et 16 est le produit.

Note : Si on veut énumérer tous les nombres naturels qui sont des facteurs de 16, il faut ajouter 1, 4 et 16 puisque \(1\; \times \;16\; = \;16\) et que \(4\; \times \;4\; = \;16\).

Dans une division, la relation entre le dividende et le diviseur donne un quotient. Un nombre naturel est dit être un diviseur d’un autre nombre naturel si leur quotient est un nombre entier. Ainsi, 3 est un diviseur de 21 puisque le quotient donne l’entier 7.

Dans l’équation 21 divisé par trois égale sept, 21 est le dividende, trois est le diviseur et sept est le quotient.

Note : Si on veut énumérer tous les diviseurs possibles de 21, il faut ajouter 1, 7 et 21 puisque \(21\; \div \;1\; = \;21\), \(21\; \div \;7\; = \;3\) et \(21\; \div \;21\; = \;1\). Les élèves pourraient constater que tout nombre naturel a au moins deux diviseurs, soit le nombre lui-même et le nombre 1.

Puisque la multiplication et la division sont des opérations inverses, il est possible d’établir des relations entre les concepts de multiple, de facteur, de dividende, de diviseur et de quotient. Par exemple, tout facteur d’un nombre est aussi un diviseur de ce nombre (4 est à la fois un facteur et un diviseur de 28). Ainsi, les relations entre les nombres peuvent être exprimées différemment selon l’analyse que l’on fait d’une situation donnée. Les élèves pourraient notamment dire que 8 est un multiple de 4, que 4 est un facteur de 8, que 8 est divisible par 4 ou que 4 est un diviseur de 8. Les élèves pourraient aussi reconnaître que le nombre 24 est un multiple de l’ensemble des nombres {1, 2, 3, 4, 6, 8, 12 et 24} et que ces nombres sont ses facteurs ou ses diviseurs.

Nombre divisible par un autre nombre

Un nombre naturel est dit être divisible par un autre nombre naturel si leur quotient est une valeur entière, c’est-à-dire qu’il n’y a pas de reste. L’habileté à reconnaître qu’un nombre est divisible ou non par un autre nombre est une composante importante du sens du nombre. En plus de favoriser la reconnaissance des relations avec de grands nombres, elle permet aux élèves de manipuler les nombres avec plus de facilité dans un contexte de résolution de problèmes. Elle leur permet par exemple de découvrir des facteurs ou des diviseurs des nombres, de regrouper les nombres plus rapidement en tenant compte du reste possible et d’explorer certains concepts qui font appel à la multiplication ou à la division (par exemple, aire).

En général, la divisibilité d’un nombre est déterminée en effectuant une division et en vérifiant s’il y a un reste ou non. Il existe cependant des règles qui permettent de déterminer rapidement la divisibilité d’un nombre par un autre nombre.

Certaines règles (par exemple, divisibilité par 2, 5 ou 10) peuvent être découvertes assez facilement par les élèves dans le cadre de situations d’apprentissage qui misent sur une analyse des multiples d’un nombre et sur la recherche de régularités et de généralisations, ce qui contribue au développement du sens du nombre.

Les règles de divisibilité par 2, 3, 4, 5, 6, 8 ou 10 sont décrites dans ce qui suit. Les explications données pour chacune visent à faire ressortir la justification mathématique derrière la règle. Il existe des règles de divisibilité pour d’autres nombres que les élèves pourraient prendre plaisir à découvrir en analysant les multiples possibles de ces nombres (par exemple, divisibilité par 9, 11, 20, 25, 50).

Règle de divisibilité par 2 : Un nombre naturel est divisible par 2 si c’est un nombre pair. Par définition, un nombre pair est un nombre divisible en deux parties égales. Puisque tout nombre pair a le chiffre 0, 2, 4, 6 ou 8 dans la position des unités, il est facile de reconnaître, par exemple, que 23 674 est divisible par 2 alors que 25 149 ne l’est pas.

Règle de divisibilité par 3 : Un nombre naturel est divisible par 3 si la somme des chiffres qui le composent est divisible par 3.

Prenons par exemple le nombre 756. La somme des chiffres qui le composent (\(7\; + \;5\; + \;6\)) donne 18, un nombre qui est divisible par 3 puisque \(18\; \div \;3\; = \;6\). On peut donc conclure que 756 est divisible par 3. En appliquant ainsi la règle mécaniquement, il est difficile de saisir pourquoi elle fonctionne. Il faut analyser comment la division par 3 s’opère pour mieux comprendre. Premièrement, il faut reconnaître que si on divise 1 000, 100 ou 10 par 3, il y aura toujours un reste de 1 (par exemple, \(100\; \div \;3\; = \;33\), reste 1). Si on analyse maintenant la division de 756 par 3, il suffit de décomposer le dividende en centaines, en dizaines et en unités, et d’examiner les restes qui résultent de chacune des divisions :

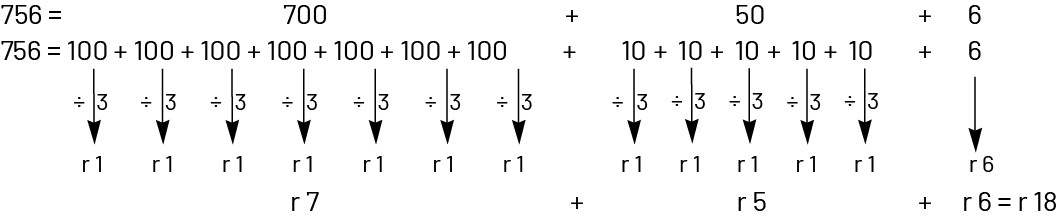
Image 756 égale 700 plus 50 plus six. 756 égale cent plus cent plus cent plus cent plus cent plus cent plus cent plus dix plus dix plus dix plus dix plus dix plus six. Sous chaque nombre cent, une flèche descend vers « r 1 » en mentionnant « divisé par trois ». Sous chaque chiffre cinq, une flèche descend vers « r 1 » en mentionnant « divisé par trois ». Sous le chiffre six, une flèche descend vers « r 6 ». Sous les sept « r 1 », il est écrit « r 7 ». Sous les cinq « r 1 », il est écrit « r 5 ». Sous « r 6 », il est écrit « r 6 ». « r 7 » plus « r 5 » plus « r 6 » égale « r 18 ».

On constate que 700 divisé par 3 donne un reste de 7 unités et que 50 divisé par 3 donne un reste de 5 unités. En additionnant ces 7 unités et ces 5 unités restantes aux 6 unités qui n’ont pas encore été divisées, on obtient 18 unités. Puisque ces 18 unités peuvent être divisées par 3 sans qu’il y ait de reste, on peut conclure que 756 est divisible par 3. Notez que la somme des restes de la division de chaque centaine (7) correspond au chiffre dans la position de centaines dans le nombre 756. Il en va de même pour la somme des restes de la division de chaque dizaine (5). Ainsi, quoique la règle de divisibilité par 3 stipule qu’il faut additionner les chiffres qui composent le nombre donné (7, 5 et 6), ce sont en réalité les restes de la division de chaque centaine, les restes de la division de chaque dizaine et le nombre d’unités qui sont additionnées.

On peut reprendre le raisonnement avec un autre nombre, par exemple avec le nombre 341. Comme à la suite de la décomposition du nombre et à la division par 3, il y aurait 3 unités restantes des centaines, 4 unités restantes des dizaines et 1 unité, pour un total de 8 unités. Puisque ces 8 unités ne peuvent pas être divisées par 3 sans qu’il y ait de reste, alors on peut conclure que 341 n’est pas divisible par 3.

Règle de divisibilité par 4 : Un nombre naturel est divisible par 4 si les deux derniers chiffres qui le composent sont divisibles par 4.

Notons d’abord que les nombres à un et à deux chiffres qui sont des multiples de 4 sont 4, 8, 12, 16, 20, 24, 28, 32, 36… 96. Ce sont donc les seuls nombres inférieurs à 100 qui sont divisibles par 4. Notons ensuite que 100 est divisible par 4. On peut alors déduire que tous les multiples de 100 sont aussi divisibles par 4 (par exemple, 600, 12 400, 706 300).

Pour déterminer si un nombre, par exemple 1 316, est divisible ou pas par 4, il suffit de le décomposer comme suit : \(1\;316\; = \;1\;300\; + \;16\). Puisque 1 300 est un multiple de 100, il est donc divisible par 4, et puisque 16 est aussi divisible par 4, on peut conclure que 1 316 est divisible par 4.

En appliquant la même règle à un autre nombre, par exemple au nombre 435 230, on peut conclure qu’il n’est pas divisible par 4. En effet, en le décomposant en \(435\;200\; + \;30\), on sait que 435 200 est divisible par 4 puisque c’est un multiple de 100. Cependant, puisque 30 n’est pas divisible par 4, on peut conclure que 435 230 n’est pas divisible par 4.

Ces deux exemples démontrent, comme l’indique la règle, qu’il suffit de vérifier la divisibilité par 4 de la partie du nombre qui est inférieure à 100, c’est-à-dire les deux derniers chiffres, pour déterminer si un nombre quelconque est divisible par 4.

Règle de divisibilité par 5 : Un nombre naturel est divisible par 5 s’il a le chiffre 0 ou 5 dans la position des unités.

Les élèves peuvent découvrir facilement cette règle en énumérant la liste des multiples de 5, soit 5, 10, 15, 20, 25, 30, 35… Elles et ils peuvent simplement observer que tous ces multiples ont un 0 ou un 5 dans la position des unités. Il est donc facile de reconnaître, par exemple, que le nombre 34 675 est divisible par 5 puisqu’il se termine par un 5 alors que le nombre 76 942 ne l’est pas.

Règle de divisibilité par 6 : Un nombre naturel est divisible par 6 s’il est divisible par 2 et par 3.

Cette règle découle du constat que tous les multiples de 6 (6, 12, 18, 24, 30, 36, 42…) sont à la fois des multiples de 2 (nombres pairs) et des multiples de 3. Ceci s’explique du fait que multiplier un nombre par 6 équivaut à le multiplier d’abord par 2, puis par 3 ou vice versa.

Ainsi, pour vérifier si, par exemple, le nombre 126 est divisible par 6, il suffit de constater qu’il est divisible par 2 (c’est un nombre pair) et par 3 (la somme des chiffres qui le composent, soit 9, est divisible par 3). Il est donc divisible par 6. Cependant, le nombre 136 n’est pas divisible par 6 puisqu’il est divisible par 2 (c’est un nombre pair), mais pas par 3 (la somme des chiffres qui le composent, soit 10, n’est pas divisible par 3). De même, le nombre 189 n’est pas divisible par 6 puisqu’il est divisible par 3 (la somme des nombres qui le composent, soit 18, est divisible par 3), mais pas par 2 (c’est un nombre impair).

Règle de divisibilité par 8 : Un nombre naturel est divisible par 8 si les trois derniers chiffres qui le composent sont divisibles par 8.

L’explication de la règle de divisibilité par 8 est semblable à celle de la divisibilité par 4. Puisque 1 000 est divisible par 8 (\(1\;000\; \div \;8\; = \;125\)), on peut déduire que tous les multiples de 1 000 (par exemple, 7 000, 34 000, 1 362 000) sont aussi divisibles par 8. La divisibilité d’un nombre par 8 dépend donc exclusivement de la divisibilité des trois derniers chiffres qui le composent.

Ainsi, pour déterminer, par exemple, si le nombre 3 160 est divisible par 8, on peut d’abord le décomposer comme suit : \(3\;000\; + \;160\). Puisque 3 000 est divisible par 8, car il est un multiple de 1 000, il suffit de déterminer si 160 est aussi divisible par 8. Puisqu’il l’est (\(160\; \div \;8\; = \;20\)), on peut conclure que 3 160 est divisible par 8.

De la même façon, pour déterminer si 879 114 (\(879\;000\; + \;114\)) est divisible par 8, il suffit de considérer le 1. Puisque 114 n’est pas divisible par 8, alors 879 114 ne l’est pas non plus.

Règle de divisibilité par 10 : Un nombre naturel est divisible par 10 s’il a le chiffre 0 dans la position des unités.

Cette règle est aussi facile à établir par les élèves. Elles et ils connaissent bien les multiples de 10 (10, 20, 30, 40…) et sont en mesure de reconnaître que chacun d’eux se termine par un 0. Une autre façon d’exprimer cette réalité est de souligner que tout nombre qui a un 0 dans la position des unités est composé exclusivement d’un certain nombre de dizaines. Par exemple, le nombre 1 360 représente 136 dizaines. Il est donc nécessairement divisible par 10.


Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 55-63.

Connaissance : divisibilité

Règle qui détermine si un nombre est divisible par un autre et qui est généralement considérée vraie dans les cas suivants :

  • Un nombre est divisible par 2 si le dernier chiffre est pair (0, 2, 4, 6 ou 8).
  • Un nombre est divisible par 3 si la somme des chiffres est divisible par 3.
  • Un nombre est divisible par 4 si les deux derniers chiffres forment un nombre divisible par 4.
  • Un nombre est divisible par 5 si le dernier chiffre est 0 ou 5.
  • Un nombre est divisible par 6 s’il est divisible par 2 et 3.
  • Un nombre est divisible par 8 si les trois derniers chiffres forment un nombre divisible par 8.
  • Un nombre est divisible par 9 si la somme des chiffres est divisible par 9. 
  • Un nombre est divisible par 10 si le dernier chiffre est 0.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.