B2.2 understand the divisibility rules and use them to determine whether numbers are divisible by 2, 3, 4, 5, 6, 8, 9, and 10
Skill: Understanding and Using Divisibility Criteria
Multiplicative and Divisibility Relationships
The multiplicative and divisibility relationships between two numbers are relationships based on multiplication and division respectively. For example, there is a multiplicative relationship between 3 and 15 since 15 is a multiple of 3, and also a divisibility relationship since 15 is divisible by 3.
From recognizing these relationships, students in the junior division can identify various characteristics of a whole number, including the fact that the number can be :
- an even number or an odd number;
- a factor and a divisor of another number;
- divisible by another number.
Studying these characteristics of whole numbers helps students develop number sense and better use numbers in
everyday situations. These characteristics are explained in more detail in the following for teachers. With students,
however, it is important to avoid getting caught up in "tricks", terminology and definitions. What is
important for students is to develop a conceptual understanding of these characteristics through activities that focus
on recognizing multiplicative or divisibility relationships.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 55.
Even or Odd numbers
If a whole number is divisible into two equal parts, it is an even number; otherwise, it is an odd number. The definition of even and odd numbers is therefore associated with the relation of divisibility or non-divisibility by two.
It is in the context of activities that students should be led to note that all whole numbers with the digit 0, 2, 4,
6 or 8 in the ones position are even numbers, while those with the digit 1, 3, 5, 7 or 9 in the ones position are odd
numbers. These observations allow them to quickly recognize whether a number is even or odd without having to check
the divisibility by two.
Source: A Guide to
Effective Instruction in Mathematics, Grades 4-6, p 55-56.
Factor and Divisor of a Number
In a multiplication of two or more whole numbers, each of these numbers is called a factor of the number that makes
up the product. For example, 2 and 8 are factors of 16.
Note: If we want to enumerate all the whole numbers that are factors of 16, we must add 1, 4 and 16 since \(1 \times \;16 = \;16\) and \(4 \times \;4 = \;16\).
In division, the relationship between the dividend and the divisor gives a quotient. A whole number is said to be a
divisor of another whole number if their quotient is a whole number. Thus, 3 is a divisor of 21 since the quotient is
7 which is a whole number.
Note: If we want to enumerate all the possible divisors of 21, we must add 1, 7 and 21 since \(21\; \div \;1\; = \;21\), \(21\; \div \; 7\; = \;3\) and \(21\; \div \;21\; = \;1\). Students may find that every whole number has at least two divisors: the number itself and the number 1.
Since multiplication and division are inverse operations, it is possible to establish relationships between the concepts of multiple, factor, dividend, divisor and quotient. For example, any factor of a number is also a divisor of that number (4 is both a factor and a divisor of 28). Thus, the relationships between numbers can be expressed differently depending on the analysis that one makes of a given situation. Students could say that 8 is a multiple of 4, that 4 is a factor of 8, that 8 is divisible by 4 or that 4 is a divisor of 8. They could also recognize that the number 24 is a multiple of set of numbers {1, 2, 3, 4, 6, 8, 12 and 24} and that these numbers are its factors or its divisors.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p 57-58.
Number Divisible by Another Number
A whole number is said to be divisible by another whole number if their quotient is an integer, i.e. there is no remainder. The ability to recognize whether or not a number is divisible by another number is an important component of number sense. In addition to fostering the recognition of relationships with large numbers, it allows students to manipulate numbers with greater ease in a problem-solving context. For example, it allows them to discover factors or divisors of numbers, to group numbers more quickly by taking into account the possible remainder, and to explore certain concepts that involve multiplication or division (for example, area).
In general, the divisibility of a number is determined by performing a division and checking whether or not there is a remainder. However, there are rules that allow you to quickly determine the divisibility of a number by another number.
Some rules (for example, divisibility by 2, 5 or 10) can be discovered quite easily by students in the context of learning situations that rely on an analysis of multiples of a number and on the search for regularities and generalizations , which contributes to the development of number sense.
The rules for divisibility by 2, 3, 4, 5, 6, 8 or 10 are described below. The explanations given for each aim to bring out the mathematical justification behind the rule. There are divisibility rules for other numbers that students might enjoy discovering by analyzing possible multiples of these numbers (for example, divisibility by 9, 11, 20, 25, 50).
Rule of divisibility by 2: A whole number is divisible by 2 if it is an even number. By definition, an even number is a number divisible into two equal parts. Since any even number has the digit 0, 2, 4, 6 or 8 in the units position, it is easy to recognize, for example, that 23,674 is divisible by 2 while 25,149 is not.
Rule of divisibility by 3: A whole number is divisible by 3 if the sum of its digits is divisible by 3.
Take for example the number 756. The sum of its digits (\(7\; + \;5\; + \;6\)) gives 18, a number which is divisible
by 3 since \(18\; \ div \;3\; = \;6\). We can therefore conclude that 756 is divisible by 3. Applying the rule in this
way mechanically, it is difficult to understand why it works. It is necessary to analyze how the division by 3
operates to better understand. First, we must recognize that if we divide 1 000, 100 or 10 by 3, there will always be
a remainder of 1 (for example, \(100\; \div \;3\; = \;33\), remainder 1). If we now analyze the division of 756 by 3,
it suffices to break down the dividend into hundreds, tens and units, and to examine the remainders which result from
each of the divisions:
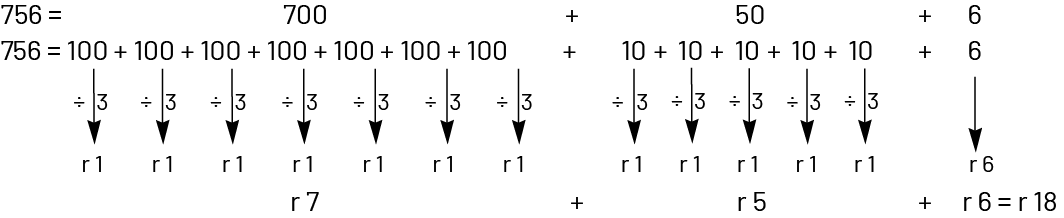
We find that 700 divided by 3 gives a remainder of 7 units and that 50 divided by 3 gives a remainder of 5 units. Adding these 7 units and these remaining 5 units to the 6 units that have not yet been divided, we get 18 units. Since these 18 units can be divided by 3 without any remainder, we can conclude that 756 is divisible by 3. Note that the sum of the remainders of the division of each hundred (7) corresponds to the digit in the position of hundreds in the number 756. The same goes for the sum of the remainders of the division of each ten (5). Thus, although the rule of divisibility by 3 stipulates that it is necessary to add the digits which compose the given number (7, 5 and 6), they are in reality the remainders of the division of each hundred, the remainders of the division of each ten and the number of units that are added.
We can resume the reasoning with another number, for example with the number 341. As following the decomposition of the number and division by 3, there would be 3 remaining units of the hundreds, 4 remaining units of the tens and 1 unit , for a total of 8 units. Since these 8 units cannot be divided by 3 without having a remainder, then we can conclude that 341 is not divisible by 3.
Rule of divisibility by 4: A whole number is divisible by 4 if the last two digits of it are divisible by 4.
Note first that the one and two digit numbers that are multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36… 96. So these are the only numbers less than 100 that are divisible by 4. Note then that 100 is divisible by 4. We can then deduce that all multiples of 100 are also divisible by 4 (for example, 600, 12 400, 706 300).
To determine whether a number, for example 1316, is divisible or not by 4, simply break it down as follows: \(1\;316\; = \;1\;300\; + \;16\). Since 1300 is a multiple of 100, so it is divisible by 4, and since 16 is also divisible by 4, we can conclude that 1316 is divisible by 4.
By applying the same rule to another number, for example to the number 435 230, we can conclude that it is not divisible by 4. Indeed, by breaking it down into \(435\;200\; + \;30 \), we know that 435,200 is divisible by 4 since it is a multiple of 100. However, since 30 is not divisible by 4, we can conclude that 435,230 is not divisible by 4.
These two examples demonstrate, as the rule indicates, that it suffices to check the divisibility by 4 of the part of the number which is less than 100, that is to say the last two digits, to determine whether a number anything is divisible by 4.
Rule of divisibility by 5: A whole number is divisible by 5 if it has the digit 0 or 5 in the units position.
Students can easily discover this rule by listing the multiples of 5, namely, 5, 10, 15, 20, 25, 30, 35… They can simply observe that all of these multiples have either a 0 or a 5 in the unit position. It is therefore easy to recognize, for example, that the number 34,675 is divisible by 5 since it ends with a 5, whereas the number 76 942 is not.
Rule of divisibility by 6: A whole number is divisible by 6 if it is divisible by 2 and by 3.
This rule is based on the fact that all multiples of 6 (6, 12, 18, 24, 30, 36, 42…) are both multiples of 2 (even numbers) and multiples of 3. This is because multiplying a number by 6 is equivalent to multiplying it first by 2 and then by 3 or vice versa.
Thus, to check if, for example, the number 126 is divisible by 6, it is enough to note that it is divisible by 2 (it is an even number) and by 3 (the sum of the digits which compose it, that is to say 9, is divisible by 3). It is therefore divisible by 6. However, the number 136 is not divisible by 6 since it is divisible by 2 (it is an even number), but not by 3 (the sum of its digits, 10, is not divisible by 3). Similarly, the number 189 is not divisible by 6 since it is divisible by 3 (the sum of the numbers that make it up, 18, is divisible by 3), but not by 2 (it is an odd number).
Rule of divisibility by 8: A whole number is divisible by 8 if the last three digits of it are divisible by 8.
The explanation of the divisibility by 8 rule is similar to that of divisibility by 4. Since 1 000 is divisible by 8 (\(1;000; \div \;8; = \;125)), we can deduce that all multiples of 1 000 (for example, 7 000, 34 000, 1 362 000) are also divisible by 8. The divisibility of a number by 8 depends exclusively on the divisibility of the last three digits of the number.
Thus, to determine, for example, whether the number 3 160 is divisible by 8, we can first decompose it as follows: \(3\;000\; + \;160\). Since 3 000 is divisible by 8, because it is a multiple of 1 000, it is sufficient to determine if 160 is also divisible by 8. Since it is (\(160; \div \;8\; = \;20\)), we can conclude that 3160 is divisible by 8.
Similarly, to determine if 879 114 (\(879\;000\; + \;114\)) is divisible by 8, just consider 114. Since 114 is not divisible by 8, then 879 114 is not either.
Rule of divisibility by 10: A whole number is divisible by 10 if it has the digit 0 in the units position.
This rule is also easy to establish by the students. They are familiar with multiples of 10 (10, 20, 30, 40…) and are able to recognize that each of them ends in a 0. Another way of expressing this reality is to point out that any number that has a 0 in the ones position is composed exclusively of a certain number of tens. For example, the number 1360 represents 136 tens. It is therefore necessarily divisible by 10.
Source: A Guide
to Effective Instruction in Mathematics, Grades 4-6, p 59-63.
Knowledge: Divisibility
A rule that determines whether a number is divisible by another and is generally considered true in the following cases:
- A number is divisible by 2 if the last digit is even (0, 2, 4, 6 or 8).
- A number is divisible by 3 if the sum of the digits is divisible by 3.
- A number is divisible by 4 if the last two digits form a number divisible by 4.
- A number is divisible by 5 if the last digit is 0 or 5.
- A number is divisible by 6 if it is divisible by 2 and 3.
- A number is divisible by 8 if the last three digits form a number divisible by 8.
- A number is divisible by 10 if the last digit is 0.
Source : The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.