B2.3 Utiliser des stratégies de calcul mental pour calculer des pourcentages de 1 %, 5 %, 10 %, 15 %, 25 % et 50 % de nombres naturels, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental pour calculer des pourcentages de 1 %, 5 %, 10 %, 15 %, 25 % et 50 % de nombres naturels
Représentation mentale
Les élèves doivent être capables de se créer une représentation mentale d’un pourcentage, comme elles et ils le font pour les nombres décimaux. La nature même du pourcentage leur permet de visualiser plus facilement une quantité, car il s’agit toujours d’un rapport avec 100. Il faut aussi bien comprendre qu’un pourcentage est une autre façon de représenter une quantité.
Exemple
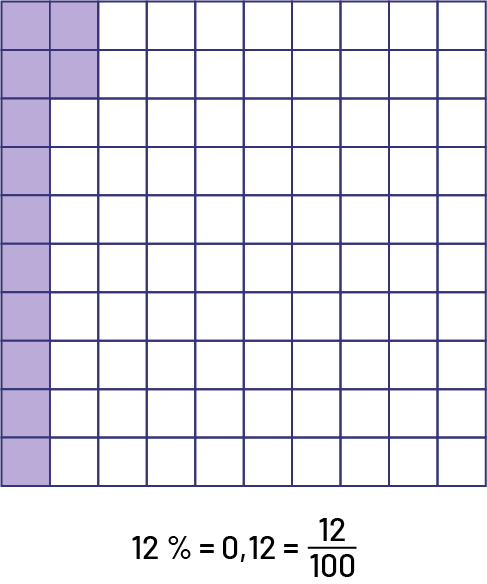
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 37.
Relation d’égalité entre un nombre décimal, la fraction décimale correspondante et le pourcentage
On sait qu’un nombre décimal représente une fraction dont le dénominateur est une puissance de 10 (par exemple, \(0,3\; = \;\frac{3}{{10}}\); \(0,47\; = \;\frac{{47}}{{100}}\)). Le concept de pourcentage étant intimement lié au concept de fraction, il n’y a qu’un pas à faire pour relier le pourcentage, le nombre décimal et la fraction décimale. Au cycle moyen, les élèves qui ont acquis un bon sens du nombre peuvent passer d’une notation à une autre sans difficulté.
Exemple
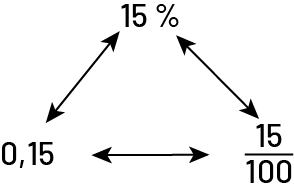
Pour aider les élèves à développer cette habileté, il faut régulièrement les inviter à exprimer leurs réponses en utilisant une autre notation. Par exemple, le personnel enseignant peut inciter l’élève qui a répondu que le \(\frac{3}{4}\) des jeunes de la classe ont les cheveux noirs à exprimer aussi cette réponse en notation décimale (0,75) et en pourcentage (75 %).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-51.
Repères
Les représentations mentales utilisées par les élèves sont renforcées par l’utilisation de repères. De façon générale, un repère est un élément de référence. Les repères utilisés pour l’étude des nombres décimaux et des pourcentages ressemblent à ceux employés pour l’étude des fractions. En créant des liens entre les nombres décimaux, les pourcentages et les repères fractionnaires, les élèves approfondissent leur sens du nombre.
Le tableau ci-après présente quelques repères qui devraient faire partie du bagage des élèves.
Repères pour les fractions, les pourcentages et les nombres décimaux
| Fraction | Pourcentage | Nombre décimal | Exemple de représentation mentale |
|---|---|---|---|
| \(\frac{1}{{ 100 }}\) | 1 % | 0,01 |  |
| \(\frac{1}{20}\) | 5 % | 0,05 |  |
| \(\frac{1}{10}\) | 10 % | 0,1 |  |
| \(\frac{15}{100}\) | 15 % | 0,15 |  |
| \(\frac{1}{4}\) | 25 % | 0,25 |  |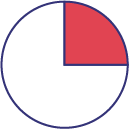
| \(\frac{1}{2}\) | 50 % | 0,5 |  |
| 1 | 100 % | 1,00 |  |
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 38-39.
Relations de proportionnalité
L’étude des nombres décimaux et des pourcentages fournit une excellente occasion d’aborder les relations de proportionnalité. Dès qu’un résultat est exprimé en pourcentage, il peut être réécrit sous forme de fraction décimale et être ensuite représenté par une fraction équivalente.
Au cycle moyen, les élèves apprennent le concept de proportions (par exemple, \(\frac{1}{4}\; = \frac{3}{{12}}\)). Il s’agit de mettre en valeur la connaissance et la compréhension qu’ont les élèves des fractions équivalentes. Les élèves qui ont assimilé le concept de fractions équivalentes peuvent utiliser les relations multiplicatives pour résoudre des problèmes comportant des proportions quand la réponse recherchée est un nombre naturel (par exemple, \(\frac{2}{{10}}\; = \frac{?}{{40}}\)).
Les relations de proportionnalité permettent de résoudre une multitude de problèmes tirés du quotidien en ayant recours à un raisonnement simple à la portée des élèves du cycle moyen. Par exemple, si 15 % des 500 élèves d’une école aiment le couscous, il est possible de déterminer, de diverses façons, qu’il y a 75 élèves qui aiment le couscous. Voici quelques exemples.
Exemple 1
Créer une représentation semi-concrète.
Je détermine tout d’abord 15 % de 100. Je sais que pour chaque tranche de 100 élèves, il y a 15 élèves qui aiment le couscous. Alors, je multiplie ce nombre par 5 pour obtenir le nombre d’élèves parmi 500 qui aiment le couscous.
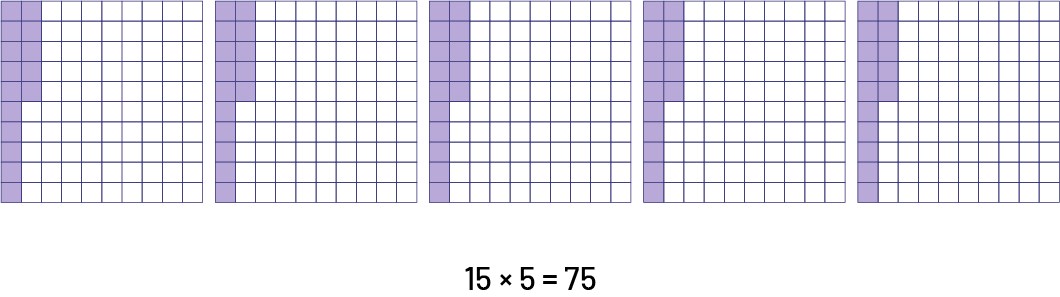
Exemple 2
Construire une table de valeurs.
Je détermine tout d’abord 15 % de 100. Je sais que pour chaque tranche de 100 élèves, il y a 15 élèves qui aiment le couscous. Je poursuis mes calculs pour 200, 300, 400 et enfin 500 élèves.
| Nombre de personnes dans l’école | Nombre de personnes aimant le couscous |
|---|---|
| 100 | 15 |
| 200 | 30 |
| 300 | 45 |
| 400 | 60 |
| 500 | 75 |
Exemple 3
Déterminer des fractions équivalentes.
Je détermine tout d’abord 15 % de 100. Je sais que pour chaque tranche de 100 élèves, il y a 15 élèves qui aiment le couscous, donc \(\frac{{15}}{{100}}\). Je multiplie le numérateur et le dénominateur par le même nombre pour obtenir des fractions équivalentes.
\(\frac{{15}}{{100}}\; = \;\frac{{30}}{{200}}\; = \;\frac{{45}}{{300}}\; = \;\frac{{60}}{{400}}\; = \;\frac{{75}}{{500}}\)
Exemple 4
Établir une proportion par multiplication.
\(\begin{array}{l}\frac{{15}}{{100}}\; = \;\frac{?}{{500}}\\\frac{{15\; \times \;5}}{{100\; \times \;5}}\; = \;\frac{{75}}{{500}}\end{array}\)
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 55-56.
Calcul mental
La vie quotidienne présente de nombreuses occasions d’effectuer des opérations sur les pourcentages. Par exemple, la taxe de vente provinciale sur les achats et les données sportives font appel aux pourcentages. L’habileté à estimer et l’habileté à calculer mentalement sont des caractéristiques du sens du nombre et du sens des opérations. Diverses stratégies de calcul mental peuvent être utilisées dont l’arrondissement, la décomposition et l’utilisation de repères. Voici quelques exemples de leur utilisation en situation de calcul mental.
Arrondissement
Exemple
Abdul achète une salade et un jus pour son dîner. Le coût est de 9 $ plus 13 % de taxe de vente provinciale. Combien coûtera approximativement le dîner d’Abdul?
Afin de connaître le coût approximatif de son dîner, Abdul peut :
- arrondir le pourcentage à 15 % (\(10\; + \;5\))
- 10 % de 9 $ est \(0,1 \times 9\; = \;0,90\;\$ \)
- 5 % est la moitié de 10 %, alors la moitié de 0,90 $ est 0,45 $.
- \(0,90\; + \;0,45\; = \;1,35\;\$ \)
Alors, \(9\;\$ \; + \;1,35\;\$ \; = \;10,35\;\$ \).
Le dîner d’Abdul coûtera un peu moins de 10,35 $ puisqu’on a arrondi les taxes vers le haut.
Décomposition
Une gérante achète une machine en rabais de 25 %. La machine coûte 184 $. Combien d’argent la gérante épargnera-t-elle?
Exemple de décomposition du pourcentage 1
- 25 % peut être décomposé en \(10 + 10\; + 5\).
- 10 % de 184 $ est la même chose que multiplier \(0,1 \times 184\), ce qui me donne 18,40.
- 5 % serait la moitié de 18,40, puisque 5 % est la moitié de 10 %. Alors, 5 % de 184 $ est 9,20 $.
- \(18,40 + 18,40 + 9,20\; = 46\;\$ \).
Exemple de décomposition du pourcentage 2
Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec le calcul de pourcentages.
Description de la vidéo
Description à venir
Exemple de décomposition du montant d’argent
- 25 % représente \(\frac{1}{4}\) de 184 $.
- 25 % ou \(\frac{1}{4}\) de 100 $ est 25 $.
- 25 % ou \(\frac{1}{4}\) de 80 $ est 20 $.
- 25 % ou \(\frac{1}{4}\) de 4 $ est 1 $.
La gérante épargnera \(25\;\$ \; + \;20\;\$ \; + \;1\;\$ \; = \;46\;\$ \).
Utilisation de repères
Exemple
Un sondage effectué auprès de 150 élèves de 6e année démontre leur couleur préférée. Voici, en partie, les résultats.
- 1 élève aime le noir.
- 7 élèves aiment le blanc.
- 14 élèves aiment l’orange.
- 72 élèves aiment le rouge.
Environ quel pourcentage d’élèves aime chaque couleur?
Afin d’estimer le pourcentage d’élève qui aime chaque couleur, on peut utiliser des pourcentages repères :
- 1 % de 150 est 1,5, alors un peu moins de 1 % des élèves aiment le noir.
- 5 % de 150 est 7,5, alors un peu moins de 5 % des élèves aiment le blanc.
- 10 % de 150 est 15, alors un peu moins de 10 % des élèves aiment l’orange.
- 50 % de 150 est 75, alors un peu moins de 50 % des élèves aiment le rouge.
Utiliser la valeur de position
Un magasin annonce que 10 % des ventes de la journée seront données à une charité communautaire. Le total des ventes est de 1 010 $. Quel est le montant qui sera donné à la charité?
- 10 % est égal à 0,1 ou à \(\frac{{10}}{{100}}\)
- 0,1 ou \(\frac{{10}}{{100}}\) de 1 000 est 100
- 0,1 ou \(\frac{{10}}{{100}}\) de 10 est 1
La charité recevra 101 $.
Connaissance : pourcentage
Le pourcentage est une façon particulière de présenter une fraction. Il est souvent employé dans la vie courante. Une expression numérique comme 30 % (qui se lit « trente pour cent ») est en réalité une autre notation du nombre trente centièmes, soit \(\frac{{30}}{{100}}\) ou 0,30. Afin de faciliter la compréhension du concept de pourcentage, il faut d’abord amener les élèves à établir le lien entre le pourcentage et la fraction dont le dénominateur est 100, et ce, à l’aide de matériel concret ou semi-concret.
Exemple
Lorsqu’exposés au concept de rapport, les élèves réaliseront qu’un pourcentage représente un rapport à 100 (par exemple, 30 % représente le rapport 30 : 100). Il est important de souligner qu’un résultat exprimé en pourcentage ne signifie pas que la quantité en question est nécessairement composée de 100 parties, comme expliqué dans le tableau suivant.
Lien entre le pourcentage et la quantité 100
| Représentation | Pourcentage | Notes pédagogiques |
|---|---|---|
  |
75 % des cercles sont verts. | Même si 75 % des cercles sont verts, cela ne veut pas dire qu'il y a 100 cercles dans l'ensemble. Par contre, s'il y avait 100 cercles, il y aurait 75 cercles verts. De plus, la fraction des cercles qui sont verts est équivalente à \(\frac{75}{100}\) (par exemple, \(\frac{3}{4}\) = \(\frac{75}{100}\) et \(\frac{150}{200}\) = \(\frac{75}{100}\)). |
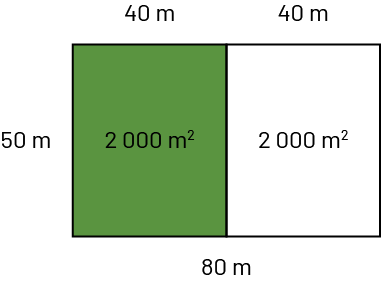 Un rectangle de 50 mètres par 80 mètres est découpé en deux parties égales sur la largeur : une partie verte et une partie blanche. Ces deux dernières mesurent respectivement 2 000 mètres carrés ainsi que 50 mètres par 40 mètres. |
50 % du terrain est recouvert de pelouse. | Même si 50 % du terrain est recouvert de pelouse, on ne peut pas affirmer que le terrain a une aire de 100 m2. Mais on peut affirmer que pour chaque 100 m2 de terrain, 50 m2 sont recouvert de pelouse. Ainsi,\(\frac{2\;000}{4\;000} \) = \(\frac{1}{2} \) = \(\frac{50}{100}\) = 50 %. |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34-35.
Connaissance : calcul mental
La plupart des calculs effectués au quotidien sont reliés à un calcul mental. Les personnes qui acquièrent de bonnes habiletés de calcul mental ne dépendent pas de l’électronique ou du papier pour effectuer les calculs de la vie courante. Or, il est important de démystifier le calcul mental. « Le calcul mental consiste à effectuer des calculs sans l’aide ou presque d’un crayon et d’un papier, ou d’une calculatrice. Il représente une composante essentielle d’un enseignement efficace au cycle moyen. » (Ministère de l’Éducation de l’Ontario, 2004 a, p. 24). Ainsi, il ne s’agit pas d’utiliser un algorithme dans sa tête, mais de calculer avec souplesse et efficacité.
Selon les situations, on fait appel au calcul mental pour déterminer des résultats approximatifs ou exacts. On estime souvent mentalement lorsque c’est l’ordre de grandeur qui est recherché. Par exemple, pour avoir une idée du coût de la taxe de ses achats, on utilise des nombres plus simples. Il est important aussi de savoir calculer mentalement avec précision (par exemple, un serveur qui doit rendre la monnaie à un client). Plusieurs stratégies de calcul mental sont basées sur la relation entre le tout et ses parties (décomposition et regroupement), sur l’établissement de relations entre les nombres et sur les propriétés des opérations. Souvent, ces stratégies proviennent d’un transfert de modèles utilisés au cours de l’apprentissage des opérations.
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 111.