B2.3 Use mental math strategies to calculate percents of whole numbers, including 1%, 5%, 10%, 15%, 25%, and 50%, and explain the strategies used.
Skill: Using Mental Math Strategies to Calculate Percents of 1%, 5%, 10%, 15%, 25% and 50% of Whole Numbers
Mental Representation
Students need to be able to create a mental representation of a percentage, as they do with decimal numbers. The very nature of a percentage makes it easier for them to visualize a quantity, as it is always a ratio to 100. It should also be understood that a percentage is another way of representing a quantity.
Example
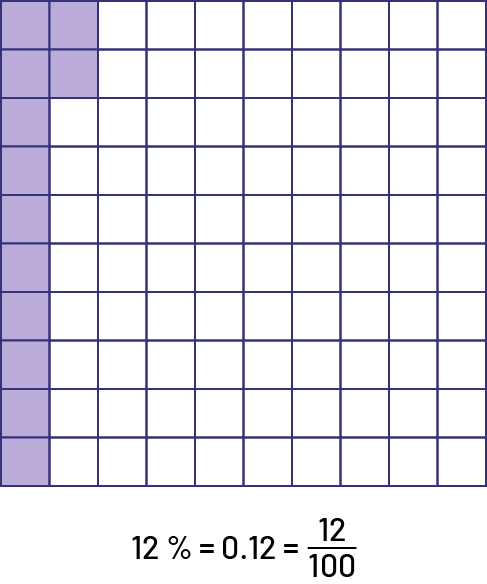
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 37.
Relationship of equality between a decimal number, the corresponding decimal fraction and the percentage
We know that a decimal number represents a fraction whose denominator is a power of 10 (for example, \(0.3\; = \;\frac{3}{{10}}\); \(0.47 \; = \;\frac{{47}}{{100}}\)). The concept of percent is closely connected to the concept of fraction, and so there is only one step to connect to decimal fractions and notation. In the Junior Division, students who have acquired a good sense of number can move from one notation to another without difficulty.
Example
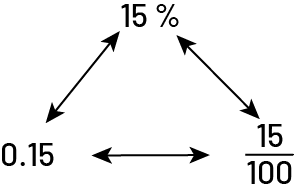
To help students develop this skill, they should be regularly invited to express their answers using another notation. For example, teachers can encourage the student who answered that the \(\frac{3}{4}\) of the young people in the class have black hair to also express this answer in decimal notation (0.75) and as a percentage (75%).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 50-51.
Benchmarks
The mental representations used by students are reinforced by the use of benchmarks. In general, a benchmark is a reference. The benchmarks for decimals and percents are similar to those used for fractions. By making connections between decimals, percents, and fraction benchmarks, students deepen their number sense.
The following table provides some benchmarks that students should know.
Benchmarks for Fractions, Percents and Decimals
| Fraction | Percent | Decimal Number | Example of a Mental Representation |
|---|---|---|---|
| \(\frac{1}{100}\) | 1% | 0.01 |  |
| \(\frac{1}{20}\) | 5% | 0.5 |  |
| \(\frac{1}{10}\) | 10% | 0.1 |  |
| \(\frac{15}{100}\) | 15% | 0.15 |  |
| \(\frac{1}{4}\) | 25% | 0.25 | 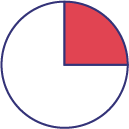 |
| \(\frac{1}{2}\) | 50% | 0.5 |  |
| 1 | 100% | 1.00 |  |
Source: Adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 38-39.
Proportional Relationships
The study of decimals and percentages provides an excellent opportunity to discuss proportionality relationships. As soon as a result is expressed as a percentage, it can be rewritten as a decimal fraction and then be represented by an equivalent fraction.
In the Junior Division, students learn the concept of proportions (for example, \(\frac{1}{4}\; = \frac{3}{{12}}\)), which enhances students' knowledge and understanding of equivalent fractions. Students who have learned the concept of equivalent fractions can use multiplicative relationships to solve problems involving proportions when the desired answer is a whole number (for example, \(\frac{2}{10}\; = \frac{?}{40}\)).
Understanding proportional relationships makes it possible to solve a multitude of everyday problems by resorting to simple reasoning. For example, if 15% of the 500 students in a school like couscous, it is possible to determine, in various ways, that there are 75 students who like couscous, as shown in the following examples.
Example 1
Use a visual (semi-concrete) representation.
First, I determine 15% of 100. I know that for every 100 students, there are 15 students who like couscous. So I multiply that number by 5 to get the number of students out of 500 who like couscous.
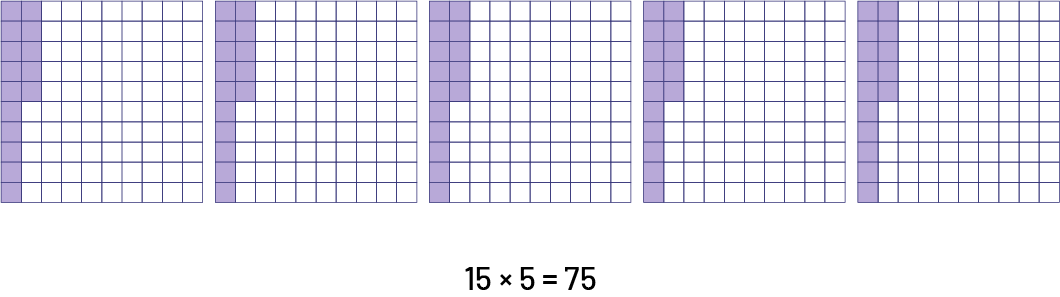
Example 2
Build a table of values.
I started with 15% of 100. I know that for every 100 students, there are 15 students who like couscous. I continued the chart for 200, 300, 400 and finally 500 students, adding 15 for every one hundred students.
| Number of people in the school | Number of people who like couscous |
|---|---|
| 100 | 15 |
| 200 | 30 |
| 300 | 45 |
| 400 | 60 |
| 500 | 75 |
Example 3
Determine equivalent fractions.
I started with the fraction \(\frac{{15}}{{100}}\) because I know that for every 100 students, there are 15 students who like couscous. I multiplied the numerator and denominator by 2 to get an equivalent fraction for 200 people, then by 3 to get an equivalent fraction for 300 people, then by 4 for 400 people, and finally by 5 for 500 people. I found that for 500 people, 75 will like couscous.
\(\frac{15}{100} = \frac{30}{200} = \frac{45}{300} = \frac{60}{400} = \frac{75}{500}\)
Example 4
Establish a proportion by multiplication.
\(\begin{array}{l}\frac{{15}}{{100}}\; = \;\frac{?}{{500}}\\\frac{{15\; \times \;5}}{{100\; \times \;5}}\; = \;\frac{{75}}{{500}}\end{array}\)
Source: Adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 55-56.
Mental Math
Everyday life presents many opportunities to perform operations with percents. For example, provincial sales tax on purchases are calculated using percents and sports data are often presented using percents. Estimation and mental math skills are characteristics of good number and operation sense. A variety of mental math strategies can be used including rounding, decomposing, and the use of benchmarks. Some examples of these strategies used in mental math situations include:
Rounding
Example
Abdul buys a salad and juice for his lunch. The cost is $9 plus 13% provincial sales tax. Approximately how much will Abdul's lunch cost?
To find out the approximate cost of his lunch, Abdul can:
- round up the percentage to 15% \((10\; + \;5)\)
- 10% of $9 is \(0.1 \times 9\;=\; \$0.90\;\)
- 5% is half of 10%, so half of $0.90 is $0.45.
- \(0.90\; + \;0.45\; = \;\$1.35\)
So, \(\$9\; + \;\$1.35\; = \;\$10.35\;\).
Abdul's lunch will cost just under $10.35 since the taxes have been rounded up.
Decomposing
A manager purchases a machine at a 25% discount. The machine costs $184. How much money will the manager save?
Example of decomposing percentages
- 25% can be decomposed into \(10 + 10\; + 5\).
- 10% of $184 is the same as multiplying \(0.1 \times 184\), which gives $18.40.
- 5% would be half of 18.40, since 5% is half of 10%. So 5% of $184 is $9.20.
- \(\$18.40\; + \$18.40\; + \$9.20\; = \$46\;\).
Example of decomposing money amount
- 25% or \(\frac{1}{4}\) of $100 is $25.
- 25% or \(\frac{1}{4}\) of $80 is $20.
- 25% or \(\frac{1}{4}\) of $4 is $1.
The manager will save \(\$25\;+ \;\$20\; + \;\$1\; = \;\$46\).
Use of Benchmarks
Example
A survey of 150 Grade 6 students shows their favourite colour. Here are some of the results.
- 1 student likes black.
- 7 students like white.
- 14 students like orange.
- 72 students like red.
About what percentage of students like each colour?
To estimate the percentage of students who like each colour, benchmark percentages can be used:
- 1% of 150 is 1.5, so a little less than 1% of students like the dark.
- 5% of 150 is 7.5, so just under 5% of students like white.
- 10% of 150 is 15, so just under 10% of students like orange.
- 50% of 150 is 75, so just under 50% of students like red.
Use the Place Value of the Digits
One store advertises that 10% of the day's sales will be donated to a community charity. The total sales are $1010. How much will be donated to the charity?
- 10% equals 0.1 or \(\frac{{10}}{{100}}\)
- 0.1 or \(\frac{{10}}{{100}}\) of 1000 is 100
- 0.1 or \(\frac{{10}}{{100}}\) of 10 is 1
The charity will receive $101.
Knowledge: Percent
A percent is a special way of presenting a fraction. It is often used in everyday life. A numeric expression like 30% (which reads "thirty percent") is actually another notation for the number thirty hundredths, either \(\frac{{30}}{{100}}\) or 0.30. To facilitate understanding of the concept of percent, students must first be introduced to the relationship between the percent and the fraction with a denominator of 100, using concrete or visual (semi-concrete) materials.
Example

When introduced to the concept of ratio, students will realize that a percentage represents a ratio of 100 (for example, 30% represents the ratio 30:100). It is important to emphasize that a result expressed as a percentage does not mean that the quantity in question is necessarily composed of 100 parts, as explained in the following table.
Relationship Between Percent and the Quantity 100
| Representation | Percentage | Instructional Notes |
|---|---|---|
  |
75% of the circles are green. | Even if 75% of the circles are green, that doesn't mean there are 100 circles overall. On the other hand, if there were 100 circles, there would be 75 green circles. Also, the fraction of circles that are green is equivalent to \(\frac{75}{100}\) (for example, \(\frac{3}{4}\) = \(\frac{75} {100}\) and if this amount were doubled, the corresponding fraction would be \(\frac{150}{200}\) = \(\frac{75}{100}\)). |
 |
50% of the site is laid to lawn. | Even if 50% of the field is covered with grass, it does not mean that the field has an area of 100 m2. The entire field is 4000 m2. If half of it is covered with grass, there would be 2000 m2 of grass. Thus, \(\frac{2\;000}{4\;000} \) = \(\frac{1}{2} \) = \(\frac{50}{100}\) = 50 %. |
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 34-35.
Knowledge: Mental Math
Most everyday calculations are related to mental math. People who develop good mental math skills do not rely on electronics or paper to perform everyday calculations. Yet, it is important to demystify mental math. "Mental math is the ability to perform calculations with little or no help from a pencil and paper or a calculator. It is an essential component of effective instruction in the junior grades." (Ontario Ministry of Education, 2004 a, p. 24). Thus, it is not about using an algorithm in your head, but about calculating flexibly and efficiently.
Depending on the situation, mental math is used to determine approximate or exact results. We often estimate mentally when we are looking for an order of magnitude. For example, to get an idea of the tax cost of one's purchases, one uses simpler numbers. It is also important to be able to calculate mentally with precision (for example, a waiter who must give change to a customer). Many mental math strategies are based on the relationship between the whole and its parts (composing, decomposing and recomposing), the relationships between and among numbers and their various representations and the relationships between operations and their properties.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 111.
