B2.6 Représenter des nombres composés sous la forme d’une multiplication de ses facteurs premiers, y compris à l’aide de l’arbre de facteurs.
Habileté : représenter des nombres composés sous forme d’une multiplication de ses facteurs premiers
Tout comme les nombres peuvent être composés et décomposés par l’addition et la soustraction, ils peuvent être composés et décomposés par la multiplication et la division (factorisation). Les facteurs d’un nombre décrivent les façons dont il peut être décomposé en parts égales par la multiplication et la division.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Un nombre composé est un nombre naturel supérieur à 1 qui possède plus de deux diviseurs entiers. Par exemple, 14 est un nombre composé, car il possède les diviseurs 1, 2, 7 et 14.
À l’opposé, un nombre premier est un nombre naturel supérieur à 1 qui a exactement deux diviseurs entiers (par exemple, 23 est un nombre premier, car il n’a comme diviseurs que 1 et lui-même). Tous les nombres naturels supérieurs à 1 sont donc soit des nombres composés, soit des nombres premiers. Quant aux nombres 0 et 1, ils ne sont par définition ni premiers ni composés.
Les élèves peuvent établir que tous les nombres premiers sauf 2 sont impairs, mais que tous les nombres impairs ne sont pas nécessairement des nombres premiers (par exemple, 9 est un nombre impair qui est composé).
L’habileté à reconnaître qu’un nombre est premier ou composé peut faciliter la résolution de problèmes.
Exemple
Les élèves doivent créer un rectangle dont les dimensions sont des valeurs entières.
Quelles sont les dimensions possibles du rectangle si son aire doit mesurer 23 cm2? 11 cm2? 24 cm2?
En reconnaissant que 23 et 11 sont des nombres premiers, les élèves peuvent justifier que dans chacun de ces deux cas, il n’existe qu’un seul ensemble de dimensions possibles (soit un rectangle de 1 cm sur 23 cm et un rectangle de 1 cm sur 11 cm).
\(11\; = \;1\; \times \;11\)
\(23\; = \;1\; \times \;23\)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 59.
Un rectangle qui a une aire de 24 cm2 peut être représenté à l’aide de rectangles de différentes dimensions.
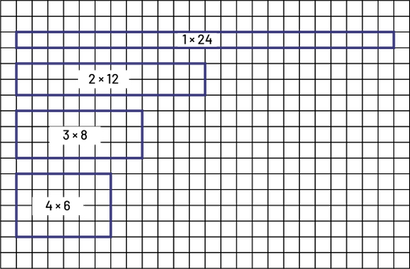Image Des rectangles sont dessinés dans une grille de 26 par 17 unités. Il y a un rectangle qui
mesure un par 24, un autre qui mesure deux par douze, un autre qui mesure trois par huit et le dernier mesure quatre
par six.On peut également démontrer que 24 est un nombre composé à l’aide d’arbres de facteurs pour arriver à ses facteurs premiers.
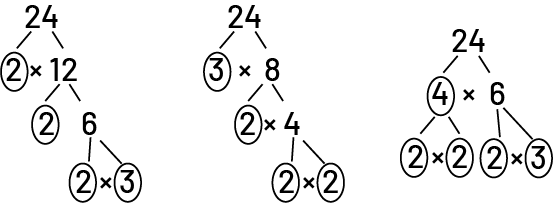
Image Trois schémas en arbre sont placés côte à côte. Ils possèdent tous le nombre 24 à leur tête. Premier schéma : 24 se lie à deux et douze dans la multiplication deux fois douze. Douze se lie à deux et six dans la multiplication deux fois six. Six se lie à deux et trois dans la multiplication deux fois trois. Tous les chiffres deux et le chiffre trois sont encerclés. Deuxième schéma : 24 se lie à trois et huit dans la multiplication trois fois huit. Huit se lie à deux et quatre dans la multiplication deux fois quatre. Et quatre se lie aux deux dans la multiplication deux fois deux. Le trois et tous les deux sont encerclés. Troisième schéma : 24 se lie à quatre et six dans la multiplication quatre fois six. Quatre se lie aux deux dans la multiplication deux fois deux, tandis que six se lie à deux et trois dans la multiplication deux fois trois. Tous les deux, le quatre et le trois sont encerclés.
\(24\; = \;2\; \times \;2\; \times \;2\; \times \;3\)
Un nombre peut être décomposé en d’autres facteurs. Les arbres de facteurs montrent les façons dont un nombre peut être décomposé jusqu’à ce que tous ses facteurs soient des nombres premiers.
Les facteurs d’un nombre peuvent aider à effectuer des calculs mentaux. Par exemple, il pourrait être difficile de calculer mentalement \(36\; \times \;4\), mais voir le produit en question comme \(4\; \times \;3\; \times \;3\; \times \;4\) signifie qu’en recourant à l’associativité, les facteurs peuvent aussi produire \(12\; \times \;12\), un fait connu.
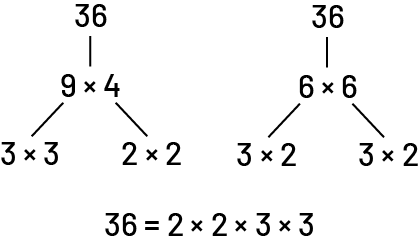
Image Deux schémas en arbre sont placés côte à côte; tous deux possèdent le nombre 36 à leur tête Premier schéma : 36 se lie à la multiplication neuf fois quatre. Neuf se lie à la multiplication trois fois trois, tandis que quatre se lie à la multiplication deux fois deux Deuxième schéma : 36 se lie à la multiplication six fois six. Les deux six se lient respectivement à une multiplication trois fois deux Sous les schémas, il est écrit : 36 égale deux fois deux fois trois fois trois.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : nombres composés
Un nombre composé est un nombre naturel supérieur à 1 qui possède plus de deux diviseurs entiers. Par exemple, 14 est un nombre composé, car il possède les diviseurs 1, 2, 7 et 14.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 59.
Connaissance : nombres premiers
Les nombres premiers ont seulement deux facteurs : 1 et eux-mêmes. Par exemple, 11 n’a que deux facteurs, 1 et 11 (\(1\; \times \;11\)), donc 11 est un nombre premier.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : arbre des facteurs
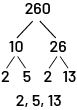
Diagramme utilisé pour trouver les facteurs d’un nombre et les facteurs de ces nombres, jusqu’à ce qu’il ne soit plus possible de trouver d’autres facteurs.
Image
Voici un schéma numérique en arbre. 260 est le nombre de tête. Il se lie à dix et à 26. Dix se lie à deux et à cinq,
tandis que 26 se lie à deux et à 13. Sous le schéma, il est écrit : deux, cinq, treize.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.