B2.6 represent composite numbers as a product of their prime factors, including through the use of factor trees
Skill: Representing Composite Numbers as a Multiplication of Prime Factors
Just as numbers can be composed and decomposed by addition and subtraction, they can be composed and decomposed by multiplication and division (factoring). The factors of a number describe the ways in which it can be broken down into equal parts by multiplication and division.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
A composite number is a whole number greater than 1 that has more than two integer divisors. For example, 14 is a composite number because it has divisors 1, 2, 7 and 14.
In contrast, a prime number is a whole number greater than 1 that has exactly two integer divisors (for example, 23 is a prime number because it has only 1 and itself as divisors). All whole numbers greater than 1 are therefore either composite numbers or prime numbers. As for the numbers 0 and 1, they are by definition neither prime nor compound.
Students can establish that all primes except 2 are odd, but that not all odd numbers are necessarily primes (for example, 9 is an odd number that is compound).
The ability to recognize that a number is prime or composite can facilitate problem solving.
Example
Students are asked to create a rectangle with dimensions that are integer values.
What are the possible dimensions of the rectangle if its area is 23 cm2? 11 cm2? 24 cm2?
Recognizing that 23 and 11 are prime numbers, students can justify that in each of these two cases there is only one set of possible dimensions (for example., a rectangle of 1 cm by 23 cm and a rectangle of 1 cm by 11 cm).
\(11; = 1; times 11)
\(23\; = \;1\; \times \;23\)
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 59.
A rectangle that has an area of 24 cm2 can be represented using rectangles of different sizes that give an area of 24 cm2.
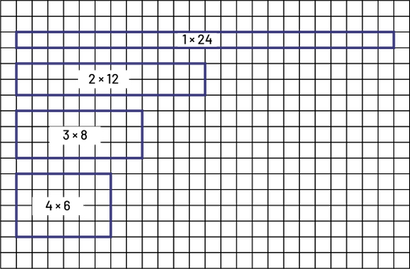
We can also show that 24 is a composite number by using factor trees to arrive at its prime factors.
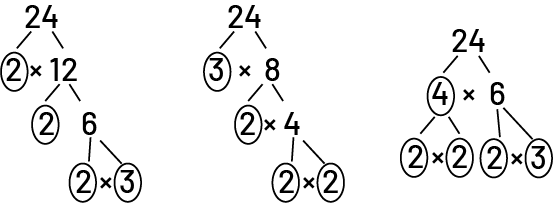
\(24\; = \;2\; \times \;2\; \times \;2\; \times \;3\)
A number can be decomposed into other factors. Factor trees show the ways in which a number can be decomposed until all its factors are prime numbers.
The factors of a number can help with mental calculations. For example, it might be difficult to mentally calculate
36; times 4, but seeing the product in question as 4; times 3; times 3; times 4 means that by using associative
property, the factors can also produce 12; times 12, a known fact.
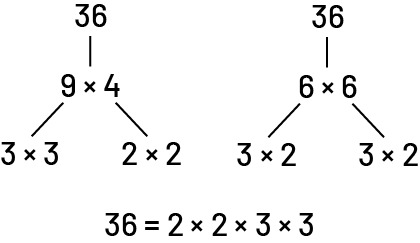
Source : The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020..
Knowledge: Composite Numbers
A composite number is a whole number greater than 1 that has more than two integer divisors. For example, 14 is a
composite number because it has divisors 1, 2, 7 and 14.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 59.
Knowledge: Prime Numbers
Prime numbers have only two factors: 1 and themselves. For example, 11 has only two factors, 1 and 11 (1; times 11), so 11 is a prime.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Knowledge: Factor Tree
Diagram used to find the factors of a number and the factors of these numbers, until no more factors can be found.
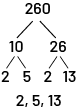
Source : The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020..