B2.7 Représenter et résoudre des problèmes relatifs à la multiplication d’un nombre naturel à trois chiffres par un nombre décimal jusqu’aux dixièmes, à l’aide d’algorithmes.
Habileté : représenter et résoudre des problèmes relatifs à la multiplication d’un nombre naturel à trois chiffres par un nombre décimal jusqu’aux dixièmes, à l’aide d’algorithmes
Les élèves du cycle moyen ont déjà une expérience du concept de multiplication et comprennent que la multiplication de nombres naturels a pour effet de générer un produit supérieur aux quantités en cause, sauf dans les situations de multiplications par 1 et par 0. Elles et ils sont alors souvent surpris de constater qu’une multiplication dont l’un des facteurs est un nombre décimal inférieur à 1 donne un produit inférieur à l’autre facteur (par exemple, \(10\; \times \;0,5\; = \;5\); \(20\; \times \;0,1\; = \;2\)).
Ces résultats sont surprenants pour quiconque ne traite pas les nombres en contexte ou n’a pas acquis une compréhension de la multiplication lui permettant d’expliquer de tels résultats.
Exemple
Si les élèves doivent déterminer la distance parcourue par un lapin qui fait 8 bonds de 0,5 m, elles et ils sont confrontés à une multiplication qui donne un produit inférieur au facteur 8, car \(0,5\; \times \;8\; = \;4\) (le lapin a fait un bond de 0,5 m huit fois). Pour évaluer l’expression \(0,5\; \times \;8\), on peut utiliser une droite numérique et représenter les 8 bonds. On obtient une distance totale de 4 m.
Image
Une droite numérique est graduée de zéro à cinq par marques d’intervalle de zéro virgule cinq. Des flèches relient
chaque marque d’intervalle à la suivante, de zéro à quatre, en indiquant zéro virgule cinq à chaque reprise.
Même s’il peut paraître surprenant que le produit soit inférieur au facteur 8, le contexte permet aux élèves d’en saisir la raison. Les élèves acquièrent alors une meilleure compréhension de la multiplication qui tient compte de telles situations.
En général, il existe deux façons d’interpréter une multiplication écrite de façon symbolique, par exemple \(3\; \times \;4\). On peut l’interpréter comme étant 3 fois le nombre 4, ce qui est équivalent à 3 groupes de 4, ou comme étant le nombre 3 multiplié par 4, ce qui est équivalent à 4 groupes de 3. Selon Baruk (1995, p. 737), une expression comme le nombre 3 multiplié par 4 est « lourde et peu en accord avec l’expression naturelle dans la langue d’une quantité qui se répète ». Dans ce document, l’expression \(3\; \times \;4\) sera interprétée comme étant 3 fois le nombre 4 ou 3 groupes de 4 afin de respecter le sens le plus naturel.
Si les élèves ont bien saisi que \(3\; \times \;4\) signifie 3 groupes de 4, elles et ils pourront comprendre le sens de 8 × 0,5, soit 8 groupes de 0,5 comme le montre l’illustration suivante dans laquelle une planchette représente l’unité.
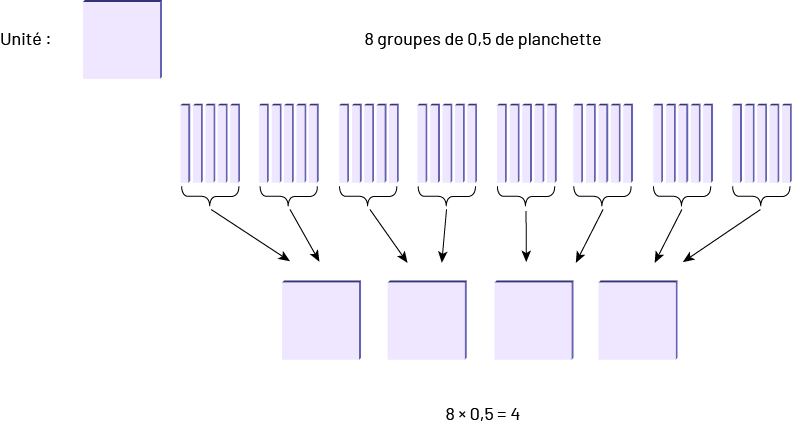Image
Dans ce schéma, un carré représente une unité. Huit groupes de zéro virgule cinq de planchette sont alignés côte à
côte. Sous ceux-ci, il y a quatre carrés. Les deux premiers groupes de demi-planchette pointent vers le premier carré
à l’aide de flèches. Les troisième et quatrième groupes de demi-planchette pointent vers le deuxième carré. Les
cinquième et sixième groupes de demi-planchette pointent vers le troisième carré. Et les septième et huitième groupes
de demi-planchette pointent vers le quatrième carré. Sous les carrés, il est écrit : huit fois zéro virgule cinq égale
quatre.
La multiplication d’un nombre naturel par un nombre décimal peut être interprétée par une addition répétée.
\(0,5 + 0,5 + 0,5 + 0,5 + 0,5 + 0,5 + 0,5 + 0,5 = 4\)
Dans l’enseignement traditionnel de la multiplication sur les nombres décimaux, on fait apprendre un algorithme. Par exemple, pour effectuer 125 × 0,1, on procède d’abord comme pour des entiers :
\(\begin{array}{l}\;\;{\kern 1pt} {\kern 1pt} 125\\\underline { \times \;0,1} \\\;\;{\kern 1pt} {\kern 1pt} 125\end{array}\)
Ensuite, on compte le nombre de décimales dans les deux facteurs (1 dans le présent exemple) et on place la virgule dans le produit afin qu’il ait le même nombre de décimales. On obtient alors :
\(\begin{array}{l}\;\;{\kern 1pt} {\kern 1pt} 125\\\underline { \times \;0,1} \\\;\,12,5\end{array}\)
Pour les élèves, il s’agit d’apprendre une règle de plus, ce qui renforce leur impression qu’apprendre les mathématiques consiste à apprendre à obéir à une multitude de règles. Or, l’apprentissage de cette règle a perdu de son importance avec l’avènement de la calculatrice. Il est plus important pour les élèves de bien intégrer les particularités de la multiplication de nombres décimaux à leurs connaissances de la multiplication de nombres naturels et d’accroître leur sens du nombre et leur sens des opérations de manière à prévoir l’ordre de grandeur du produit de deux nombres donnés.
Au départ, il est très important de comprendre un élément du sens du nombre, soit la relation d’ordre de grandeur
entre deux nombres composés des mêmes chiffres dans le même ordre. Cette relation peut être reconnue en observant la
position de la virgule dans les nombres.
Exemple
C’est en développant et en utilisant leur sens du nombre que les élèves apprennent à déterminer la position de la virgule dans le produit et non en apprenant une règle de plus. Voici des exemples de l’utilisation de l’estimation pour déterminer la position de la virgule dans un produit.
Image Un tableau possède trois colonnes : Opération, Estimation, Produit. Dans la colonne opération il est écrit : « cinq fois 25 », avec une flèche pointant à droite, et « cinq fois deux virgule cinq », avec une flèche pointant à droite. Dans la colonne Estimation, vis-à-vis la première flèche, il est écrit : « cinq groupes de 25, donc 125 »; et vis-à-vis la deuxième flèche, il est écrit : « cinq groupes de deux, soit environ dix ». Dans la colonne estimation, il est écrit, entre parenthèses : « puisque les chiffres un, deux et cinq se retrouvent dans cet ordre dans le produit. » En dessous, il y a une flèche pointant à droite vers le nombre 125. Sous ceci, il y a une flèche pointant à droite vers le nombre douze virgule cinq.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la
6e année, p. 79-83.
Lorsque les élèves représentent la multiplication d’un nombre naturel par un nombre décimal de façon concrète ou semi-concrète (par exemple, à l’aide de matériel de base dix, d’une droite numérique, d’une disposition rectangulaire), elles et ils saisissent mieux le sens de la multiplication. Les stratégies pour multiplier les nombres décimaux sont essentiellement les mêmes que celles utilisées pour multiplier les nombres naturels. Voici différentes stratégies de multiplication d’un nombre naturel par un nombre décimal.
Exemple
\(300 \times 1,3\)
Afin d’estimer le produit, il est possible de raisonner comme suit : 1,3 se situe entre 1 et 2; donc \(300 \times 1,3\), c’est entre 300 (\(300\; \times \;1\)) et 600 (\(300\; \times \;2\)). Il y a un peu plus qu’un groupe de 300.
Multiplication à l’aide de la décomposition
Je décompose 1,3 en \(1\; + \;0,3\). Je multiplie \(300 \times 1\).
Ensuite, je décompose 0,3 en \(0,1\; + \;0,1\; + \;0,1\) puisque je sais que 0,1 de 300 est 30. Alors, j’additionne \(30\; + \;30\; + \;30\; = \;90\).
\(\begin{align} 300 \times 0,3 &= 300 \times (0,1 + 0,1 + 0,1) \\ &= (300 \times 0,1) + (300 \times 0,1) + (300 \times 0,1) \\ &= 30 + 30 + 30 \\ &= 90\end{align}\)
\(\;\;300 \times 1 \;\ = 300\)
\(\;\;300 + 90 = 390\)
Multiplication à l’aide d’une disposition rectangulaire
J’ai décomposé les deux facteurs, 1,3
en \(1\; + \;0,3\) pour les rangées et 300 en \(100\; + \;100\; + \;100\) pour les colonnes.
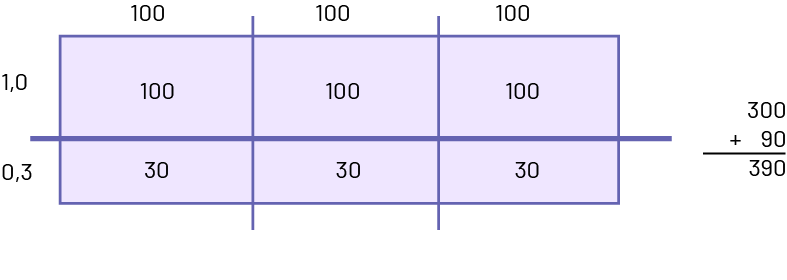Image Un
rectangle est divisé en six parties. Dans le sens de la largeur, la partie du haut mesure un virgule zéro et la partie
du bas mesure zéro virgule trois. Dans le sens de la longueur, les trois parties mesurent chacune cent. Dans chacune
des trois parties du haut, il est écrit cent; tandis que dans chacune des trois parties du bas, il est écrit trente. À
droite du rectangle, il est écrit : 300 plus 90 égale 390.
J’ai multiplié chaque centaine par un (\(100\; + \;100\; + \;100\)).
Ensuite, j’ai multiplié chaque centaine par 0,3 (\(30\; + \;30\; + \;30\)).
\(300\; + \;90\; = \;390\).
Multiplication à l’aide d’une droite numérique
Image Une
droite numérique est graduée de zéro à 500 avec marques d’intervalles de 50. Une flèche relie zéro à 300 en indiquant
300. Une flèche part de 300 et s’arrête entre 300 et 350 en indiquant 30. Une flèche part entre 300 et 350 et s’arrête
légèrement passé 350 en indiquant 30. Et une flèche part légèrement passé 350 et s’arrête à 390 en indiquant 30.
\(1\; \times \;300\; = \;300\)
\(\begin{align} 300 \times 0,3 \; &= 300 \times (0,1 + 0,1 + 0,1) \\ &= (300 \times 0,1) + (300 \times 0,1) + (300 \times 0,1) \\ &= 30 + 30 + 30 \\ &= 90\end{align}\)
Multiplication à l’aide d’un algorithme personnel
Les calculs sont effectués en partant de la gauche et selon la valeur de position.
Image
Raisonnement de l’élève. Un : J’ai 300 groupes de 1. J’écris 300 au bas. Deux : J’ai 300 groupes de zéro virgule zéro
trois, ce qui fait 90 ou neuf dizaines. J’écris cela au bas. Trois : J’additionne les réponses partielles. J’ai trois
centaines et neuf dizaines. J’obtiens 390. 300 fois un virgule trois égale 300 plus 90 égale 390.
Multiplication à l’aide de l’algorithme usuel de la multiplication
Image
Raisonnement de l’élève. Un : J’ai 300 groupes de 1. J’écris 300 au bas. Deux : J’ai 300 groupes de zéro virgule zéro
trois, ce qui fait 90 ou neuf dizaines. J’écris cela au bas. Trois : J’additionne les réponses partielles. J’ai trois
centaines et neuf dizaines. J’obtiens 390. 300 fois un virgule trois égale 300 plus 90 égale 390.
Note : Dans le cas de l’algorithme usuel, il est important que les élèves n’apprennent pas une procédure par cœur, mais qu’elles et ils comprennent chacune des étapes de la procédure et qu’elles et ils puissent l’expliquer et l’associer à une représentation concrète ou semi-concrète.
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 104-107.
Connaissance : rôle de la virgule
La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.
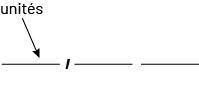
La position des unités définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, **les** centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.
Image
Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le
mot « unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les dixièmes représentent une quantité dix fois plus petite que l’unité.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 51.
Connaissance : algorithme
Les algorithmes sont des ensembles de règles et d’actions ordonnées nécessaires à la résolution d’une addition, d’une soustraction, d’une multiplication ou d’une division. En termes simples, un algorithme est la « recette » d’une opération. (Kilpatrick, Swafford et Findell, 2001, p. 103)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 75.
Connaissance : algorithme usuel
Méthode standardisée pour effectuer une opération.
Exemple
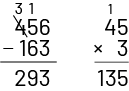Image
Deux opérations sont présentées verticalement, côte à côte. Une soustraction : 456 moins 163 égale 293. Un « un » est
retenu en haut de la colonne des dizaines. Le quatre de 456 est barré et un trois trône au-dessus. Une multiplication
: 45 fois trois égale 135. Un « un » est retenu au-dessus des dizaines.
Connaissance : algorithme personnel
Stratégie, généralement développée par l’élève, pour effectuer une opération.
Exemple
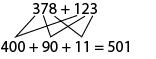Image
Deux additions sont écrites l’une au-dessus de l’autre. Première addition : 378 plus 123. Deuxième addition : 400 plus
90 plus 11 égale 591. 378 se relie à 400, 90 et 11, et chacun d’eux se relient à 123.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la
6e année, p. 75-76.