B2.7 Represent and solve problems involving the multiplication of three-digit whole numbers by decimal tenths, using algorithms.
Skill: Representing and Solving Problems Involving the Multiplication of Three-Digit Whole Numbers by Decimal Tenths, Using Algorithms
Junior students already have experience with multiplication and understand that multiplying whole numbers results in a product that is greater than the quantities involved, except in situations involving multiplying by 1 and by 0. They are then often surprised to find that a multiplication in which one of the factors is a decimal number less than 1 will result in a product less than the other factor (for example, \(10\; \times \;0.1\; = \;1\;{\rm{and}}\;{\rm{20}}\; \times \;{\rm{0}}{\rm{,10}}\;{\rm{ = } }\;{\rm{2}}\)).
These results are surprising to anyone who does not deal with numbers in context or has not developed an understanding of how different kinds of numbers behave when they are multiplied.
Example
If the students need to determine the distance traveled by a rabbit which makes 8 jumps of 0.5 m, they are confronted with a multiplication which gives a product less than the factor 8, because \(0.5\; \times \; 8\; = \;4\) (the rabbit jumped 0.5 m eight times). To evaluate the expression \(0.5\; \times \;8\), we can use a number line and represent the 8 leaps of 0.5 m. A total distance of 4 m is obtained.

While it may seem surprising that the product is less than a factor of 8, the context allows students to understand why. Students then develop a better understanding of multiplication that accounts for such situations.
In general, there are two ways to interpret a symbolically written multiplication, for example \(3\; \times \;4\). It can be interpreted as being 3 times the number 4, which is equivalent to 3 groups of 4, or as the number 3 multiplied by 4, which is equivalent to the number 3 repeated 4 times. According to Baruk (1995, p. 737), an expression like the number 3 multiplied by 4 is "heavy and not in accordance with the natural expression in the language of a repeating quantity". In this resource, the expression \(3\; \times \;4\) is interpreted as being 3 times the number 4 or 3 groups of 4 to respect the most natural meaning.
If the students understand that \(3\; \times \;4\) means 3 groups of 4, they will be able to understand the meaning of 8 × 0.5, or 8 groups of 0.5 as shown in the following illustration in which a flat represents one whole.
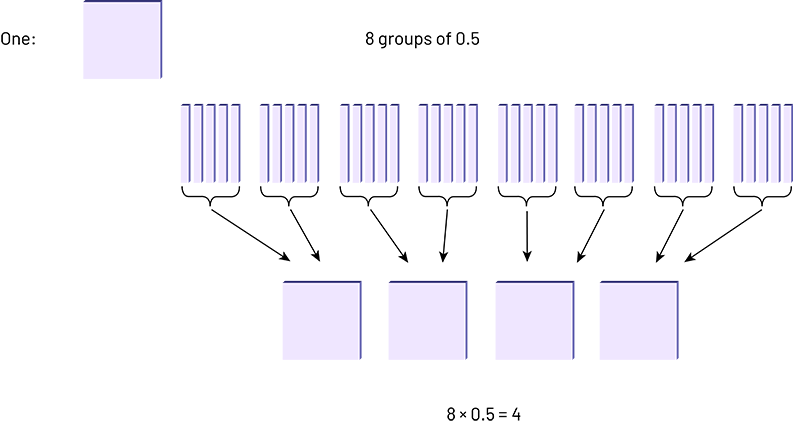
Multiplying a whole number by a decimal number can be interpreted as repeated addition.
\(0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 = 4\)
In traditional decimal multiplication teaching, an algorithm is taught. For example, to perform \(0.1\; \times \;125\), first proceed as for whole numbers:
\(\begin{array}{l}\;\;{\kern 1pt} {\kern 1pt} 125\\\underline { \times \;0,1} \\\;\;{\kern 1pt} { \kern 1pt} 125\end{array}\)
Next, count the number of decimal places in both factors (1 in this example) and place the decimal point in the product so that it has the same number of decimal places. We then obtain:
\(\begin{array}{l}\;\;{\kern 1pt} {\kern 1pt} 125\\\underline { \times \;0,1} \\\;\,12,5\end{array}\)
For students, it is just another rule to learn, which reinforces their impression that learning mathematics is about learning to obey a multitude of rules. The importance of learning this rule has diminished with the advent of the calculator. It is more important for students to integrate the specifics of decimal multiplication with their knowledge of whole number multiplication and to develop their number sense and sense of operations so that they can predict the magnitude of the product of two given numbers.
At the outset, it is very important that students understand the impact of multiplying or dividing a whole number by another whole number versus a decimal number.
Example

Students should learn to determine the position of the decimal point in the product by developing and using their number sense. The following are examples of using estimation to determine the position of the decimal point in a product.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 79-83.
When students represent the multiplication of a whole number by a decimal number in a concrete or visual way (for example, using base ten blocks, a number line, an array), they better grasp the meaning of multiplication. The strategies for multiplying decimal numbers are essentially the same as those used for multiplying whole numbers.
Example
\(300 \times 1.3\)
In order to estimate the product, it is possible to reason as follows: 1.3 is between 1 and 2; so \(300 \times 1.3\) is between 300 (\(300\; \times \;1\)) and 600 (\(300\; \times \;2\)). There is a little more than a group of 300.
Multiplication Using Decomposition
I decomposed 1.3 into \(1\; + \;0.3\). I multiplied \(300 \times 1\).
Then I decomposed 0.3 into \(0.1\; + \;0.1\; + \;0.1\). I know that 0.1 of 300 is 30, so I added \( 30\;+\;30\;+\;30\;=\;90\).
\(\begin{align} 300 \times 0.3 &= 300 \times (0.1 + 0.1 + 0.1) \\ &= (300 \times 0.1) + (300 \times 0.1) + (300 \times 0.1) \\ &= 30 + 30 + 30 \\ &= 90\end{align}\)
\(\;\;300 \times 1 \;\ = 300\)
\(\;\;300 + 90 = 390\)
Multiplication Using an Array
"I have decomposed the two factors into 1 and 0.3 for the rows, and into 100 and 100 and 100 for the columns.

I multiplied each hundred by one (\(100\; + \;100\; + \;100\)).
Then I multiplied each hundred by 0.3 (\(30\; + \;30\; + \;30\)).
\(300\; + \;90\; = \;390\).
Multiplication Using a Number Line

\(1 \times \;300 = \;300\)
\(\begin{align} 300 \times 0.3 \; &= 300 \times (0.1 + 0.1 + 0.1) \\ &= (300 \times 0.1) + (300 \times 0.1) + (300 \times 0.1) \\ &= 30 + 30 + 30 \\ &= 90\end{align}\)
Multiplication Using a Personal Algorithm
The calculations are made starting from the left and according to the place value.

Multiplication Using the Standard Algorithm

In the case of the standard algorithm, it is important that students do not learn a procedure by heart, but that they understand each step of the procedure and can explain it and associate it with a concrete or visual representation.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 104-107.
Knowledge: Role of the Decimal Point
The decimal point plays a significant role in decimal notation. It separates the whole part from the decimal part.
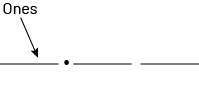
The position of the ones defines the whole according to which are formed on the one hand the tenths, the hundredths and the thousandths and on the other hand the tens, the hundreds and the thousands. It can therefore be said that the ones, identified by the decimal point, is at the heart of the decimal system.

This recognition of the role of the ones digit is evidenced by the names given to the place value of the digits on either side of it. Thus, the tenths represent a quantity ten times smaller than one and the tens are ten times bigger.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 51.
Knowledge: Algorithm
Algorithms are sets of rules and ordered actions needed to perform an addition, subtraction, multiplication or division. In simple terms, an algorithm is the "recipe" for an operation. (Kilpatrick, Swafford and Findell, 2001, p. 103)
Knowledge: Standard Algorithm
Standardized method for performing an operation.
Example

Knowledge: Student-Generated Algorithm
A strategy for solving a problem or performing a calculation, usually developed by a student.
Example
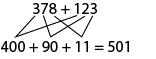
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 75-76.
