B2.8 Représenter et résoudre des problèmes relatifs à la division d’un nombre naturel à trois chiffres par un nombre décimal jusqu’aux dixièmes, à l’aide d’outils et de stratégies appropriés, et d’algorithmes, et exprimer le reste de façon appropriée.
Habileté : représenter et résoudre des problèmes relatifs à la division d’un nombre naturel à trois chiffres par un nombre décimal jusqu’aux dixièmes
Au cours de leur apprentissage, les élèves ont appris qu’une division comme \(12\; \div \;3\) s’effectue selon un contexte où l’on crée des groupes de 3 éléments (sens de groupement) ou selon celui où l’on crée 3 groupes égaux (sens de partage). Ces deux contextes existent aussi en présence d’une division d’un nombre naturel par un nombre décimal.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83.
Cependant, lors d’une division d’un nombre naturel par un nombre décimal, les contextes appellent en général à une division qui a le sens de groupement, la question étant : « Combien de dixièmes y a-t-il dans cette quantité? ».
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
Un ruban mesurant 110 cm est coupé en morceau de 5,5 cm pour fabriquer des boucles. Combien de boucles peuvent être créées?
\(110\; \div \;5,5\; = \;?\)
Estimation
\(\begin{align}110\; \div \;5,5\; &\approx \;100\; \div \;5\\ &\approx \;20\end{align}\)
- Division effectuée à l’aide d’une multiplication
\(\begin{align} 5,5\; \times ? \; &= 110 \\ 5\; \times 20 \; &= 100\\ 0,5 \times 20 &= 10 \\100 + 10 &= 110 \end{align}\)
Alors, \(5,5 \times 20 = 110\)
20 boucles peuvent être créées.
- Division effectuée à l’aide d’une disposition rectangulaire
Image
Un rectangle est traversé par une ligne horizontale juste au-dessus de sa base. Au-dessus du rectangle, il est écrit
le nombre 20 encerclé en rouge. À l’intérieur, il est écrit cent. À droite, il est écrit 110 avec une accolade qui
englobe toute sa largeur. En bas, il est écrit dix avec une flèche qui pointe vers la ligne horizontale. À gauche,
entre la base et la ligne horizontale, il est écrit zéro virgule cinq. Et à gauche au-dessus de la ligne horizontale,
il est écrit cinq.
Il est possible d’effectuer la division d’un nombre naturel par un nombre décimal en utilisant diverses stratégies, stratégies qui sont essentiellement les mêmes que celles utilisées dans les situations de divisions avec des nombres naturels. Cependant, il est important que les élèves interprètent correctement le résultat. Pour ce faire, elles et ils doivent se référer à l’estimation faite au préalable afin de s’assurer de l’ordre de grandeur du quotient. Elles et ils doivent aussi se référer à la situation-problème afin de s’assurer du sens à donner au quotient, à savoir que le résultat obtenu représente la taille des groupes ou qu’il représente le nombre de groupes. Les élèves doivent aussi comprendre et être en mesure d’expliquer la stratégie retenue pour effectuer l’opération.
Souvent, lorsque la division d’un nombre décimal représente le sens de groupement, l’opération n’est pas effectuée selon ce sens puisque représenter un raisonnement de groupement exige la création et l’interprétation d’une partie d’un groupe, ce qui rend la démarche plus difficile à saisir.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 107-108.
Une stratégie pour diviser des nombres naturels par un nombre décimal consiste à créer une division équivalente utilisant des nombres naturels.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
Min lit un livre de 135 pages. Son objectif est de lire ce livre en 4,5 jours. Combien de pages doit-elle lire par jour afin de réussir son objectif?
Estimation
\(\begin{align}135\; \div \;4,5\; &\approx \;135\; \div \;5\; \\ &\approx \;\left( {100\; \div \;5} \right)\; + \;\left( {35\; \div \;5} \right)\\ &\approx \;20\; + \;7\\ &\approx \;27\end{align}\)
- Division effectuée à l’aide d’une division équivalente
Il faut diviser 135 pages par 4,5 jours. Une division équivalente utilisant des nombres naturels est \(1\;350\; \div \;45\), puisque je multiplie chaque nombre par 10 pour éliminer la virgule.
\(\begin{align} 135 \times 10 &= 1\;350\\ 4,5\; \times \;10\; &= \;45 \\ 1\;350\; \div \;45 &= \;30 \end{align}\)
Alors, \(135 \div 4,5 = 30\)
Min doit lire 30 pages par jour.
- Division effectuée à l’aide de la disposition rectangulaire
Image
Un rectangle est traversé par une ligne horizontale juste au-dessus de sa base. Au-dessus du rectangle, il est écrit
le nombre 30 encerclé en rouge. À l’intérieur, il est écrit 120. À droite, il est écrit 135 avec une accolade qui
englobe toute sa largeur. En bas, il est écrit 15 avec une flèche qui pointe vers la ligne horizontale. À gauche,
entre la base et la ligne horizontale, il est écrit zéro virgule cinq. Et à gauche au-dessus de la ligne horizontale,
il est écrit quatre.
Le reste
Dans une division, le concept de reste survient lorsque le quotient n’est pas un nombre entier. Pour plusieurs élèves, le reste n’est qu’un nombre qui paraît dans la « recette » de la division (par exemple, \(178\; \div \;0,8\; = \;222\;{\rm{reste}} \ 4\)).
Cependant, lorsque l’opération surgit d’un contexte, le reste doit être traité afin de pouvoir répondre adéquatement au problème. Ainsi, les élèves peuvent développer l’habileté à traiter le reste si elles et ils sont en situation de résolution de problèmes. Voici plusieurs façons de traiter le reste.
- Le reste est réparti équitablement et exprimé sous la forme d’un nombre décimal.
- Le reste est réparti équitablement et exprimé sous la forme d’une fraction.
- Le reste est réparti parmi les groupes.
- Le reste entraîne la majoration du quotient de 1.
- Le reste est la réponse.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 86-87.
Connaissance : nombre décimal
Un nombre décimal est un nombre qui peut être exprimé en notation décimale avec une partie décimale finie.
Exemple
3,72 et 12,135 64
L’ensemble des nombres décimaux inclut tous les entiers, car ces derniers peuvent être exprimés avec une partie décimale.
Exemple
\(3\; = \;3,0\)
Il inclut aussi certaines fractions, comme \(\frac{2}{5}\) et \(\frac{3}{{16}}\), puisque \(\frac{2}{5}\; = \;0,4\) et \(\frac{3}{{16}}\; = \;0,187\;5\). On remarque alors que \(\frac{1}{2}\), \(\frac{5}{{10}}\) et 0,5 sont des représentations symboliques du même nombre décimal.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
Connaissance : rôle de la virgule
La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.
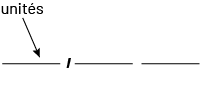
La position des unités définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, les centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.
Image
Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le
mot « unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots «
centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les dixièmes représentent une quantité dix fois plus petite que l’unité.
Image Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes,
centièmes, millièmes. Le mot « dixièmes » est encadré. Les mots « milliers » et « millièmes » sont réunis par un
trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».
Connaissance : algorithme
Les algorithmes sont des ensembles de règles et d’actions ordonnées nécessaires à la résolution d’une addition, d’une
soustraction, d’une multiplication ou d’une division. En termes simples, un algorithme est la « recette » d’une
opération. (Kilpatrick, Swafford et Findell, 2001, p. 103)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année,
p. 75.
Traditionnellement, les algorithmes (étapes de calcul standardisées) ont été conçus à une époque où une élite de « calculateurs humains » ne disposait pas de calculatrices (Ma, 2004). Les algorithmes n’étaient pas conçus pour favoriser le niveau de compréhension que nous attendons aujourd’hui des élèves. (Ministère de l’Éducation de l’Ontario, 2004 a, p. 13)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 118.
Algorithme usuel
Méthode standardisée pour effectuer une opération.
Exemple
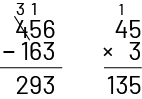Image
Deux opérations sont présentées verticalement, côte à côte. Une soustraction : 456 moins 163 égale 293. Un « un » est
retenu en haut de la colonne des dizaines. Le quatre de 456 est barré et un trois trône au-dessus. Une multiplication
: 45 fois trois égale 135. Un « un » est retenu au-dessus des dizaines.
Algorithme personnel
Stratégie, généralement développée par l’élève, pour effectuer une opération.
Exemple
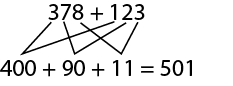Image
Deux additions sont écrites l’une au-dessus de l’autre. Première addition : 378 plus 123. Deuxième addition : 400 plus
90 plus 11 égale 591. 378 se relie à 400, 90 et 11, et chacun d’eux se relient à 123.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la
6e année, p. 76.