B2.8 represent and solve problems involving the division of three-digit whole numbers by decimal tenths, using appropriate tools, strategies, and algorithms, and expressing remainders as appropriate
Skill: Representing and Solving Problems Involving the Multiplication of Three-Digit Whole Numbers by Decimal Tenths
In the course of their learning, students have learned that a division such as (12;div; 3) is performed in a context
of creating groups of 3 elements (grouping sense) or in a context of creating 3 equal groups (sharing sense). These
two contexts also exist in the presence of a division of a whole number by a decimal number.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 83.
However, when dividing a whole number by a decimal number, the contexts usually call for a division that has the sense of grouping, the question being, "How many tenths are there in this quantity?".
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example
A ribbon measuring 110 cm is cut into 5.5 cm pieces to make loops. How many loops can be created?
\(110 \div 5.5 = \;?\)
Estimate
\(\begin{align}110\; \div \;5.5\; &\approx \;100\; \div \;5\\ &\approx \;20\end{align}\)
Division Using Multiplication
\(5.5 \times ? = 110\)
\(5 \times 20 \; = 100\)
\(0.5 \times 20 = 10\)
\(100 + 10 = 110\)
Then, \(5.5 \times 20 = 110\)
20 loops can be created.
Division Using an Area Model
Division of a whole number by a decimal number can be performed using a variety of strategies, strategies that are essentially the same as those used in division situations with whole numbers. However, it is important that students interpret the result correctly. To do this, they must refer to the estimation made beforehand to ensure the order of magnitude of the quotient. They must also refer to the context to ensure that the quotient makes sense, namely, that the result obtained represents the size or number of groups. Students must also understand and be able to explain the strategy used to perform the operation.
Often, when dividing a decimal number represents the grouping sense, the operation is not performed according to that
direction since representing a grouping reasoning requires the creation and interpretation of a part of a group, which
makes the process more difficult to grasp.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p 107-108.
One strategy for dividing whole numbers by a decimal number is to create an equivalent division using whole
numbers.
Source : The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020..
Example
Min is reading a 135 page book. Her goal is to read this book in 4.5 days. How many pages does she need to read per day in order to achieve her goal?
Estimate
\(\begin{align}135\; \div \;4,5\; &\approx \;135\; \div \;5\; \\ &\approx \;\left( {100\; \div \;5} \right)\; + \;\left( {35\; \div \;5} \right)\\ &\approx \;20\; + \;7\\ &\approx \;27 \end{align}\)
- Division Using an Equivalent Division
Divide 135 pages by 4.5 days. An equivalent division using whole numbers is \(1\;350\; \div \;45\), since I multiply each number by 10 to eliminate the decimal point.
\(\begin{array}{l}135\; \times \;10\; = \;1\;350\\4.5\; \times \;10\; = \;45\end{array} \)
\(\begin{array}{l}1\;350 \div \;45 = \;30 \end{array}\)
Then, \(135 \div 4.5 = 30\)
Min has to read 30 pages a day.
- Division Using an Area Model
The Remainder
In division, the concept of remainder arises when the quotient is not a whole number. For many students, the
remainder is just a number that appears in the “recipe” for division (for example, \(178\; \div \;0.8\; = \;222\;{\rm
{rest}}4\)).
However, when the operation arises from a context, the rest must be processed in order to adequately address the
problem. Thus, students can develop the ability to process the rest if they are in a problem-solving situation. Here
are several ways to process the remainder.
- The remainder is divided equally and expressed as a decimal number.
- The remainder is divided equally and expressed as a fraction.
- The remainder is distributed among the groups.
- The remainder increases the quotient by 1.
- The remainder is the answer.
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p 86-87.
Knowledge: Decimal Number
A decimal number is a number that has a decimal point, such as 3.75. The part before the decimal point represents a whole number amount, and the part after the decimal point represents a value that is less than one.
Example
3.72 and 12.135 64
The set of decimal numbers includes all whole numbers, because whole numbers can be expressed with a decimal part.
Example:
\(3\; = \;3,0\)
It also includes some fractions, such as \(\frac{2}{5}\ and \frac{3}{16}\), since \(\frac{2}{5}\; = \;0.4\) and \(\frac{3}{16} = \;0.187\;5\). We notice then that \(\frac{1}{2}\), \(\frac{5}{10}\) and 0,5 are symbolic representations of the same decimal number.
Source: A Guide to Effective Instruction in Mathematics Grades 4-6, p. 28.
Knowledge: Role of the Decimal Point
The decimal point plays a significant role in decimal notation. It separates the whole part from the decimal part.
The position of the ones defines the whole according to which are formed on the one hand the tenths, the hundredths and the thousandths and on the other hand the tens, the hundreds and the thousands.It can therefoere be said that the ones, identified by the decimal point, is at the heart of the decimal system.
This recognition of the role of the units digit is evidenced by the name prefixes given to the place value of the digits on either side of the unit. Thus, tenths represent a quantity ten times smaller than the unit.
Knowledge: Algorithm
Algorithms are sets of rules and ordered actions needed to solve an addition, subtraction, multiplication or
division. In simple terms, an algorithm is the "recipe" for an operation. (Kilpatrick, Swafford, &
Findell, 2001, p. 103)
Source: A Guide to Effective
Instruction in Mathematics in Grades 4-6, p. 75.
Traditionally, algorithms (standardized computational steps) were designed at a time when an elite group of
"human calculators" did not have calculators (Ma, 2004). Algorithms were not designed to foster the level of
understanding that we expect of students today. (Ontario Ministry of Education, 2004a, p. 13)
Source: A Guide to Effective Instruction in Mathematics, Grades 4-6, p. 118.
Usual Algorithm
Standardized method for performing an operation.
Example:
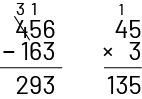
Student-Generated Algorithm
A strategy for solving a problem or performing a calculation, usually developed by the student.
Example
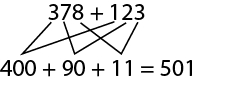
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p.
76.