B2.9 Multiplier des nombres naturels par des fractions propres, à l’aide d’outils et de stratégies appropriés.
Habileté : multiplier des nombres naturels par des fractions propres, à l’aide d’outils et de stratégies appropriés
Au cycle moyen, les élèves ont déjà un bagage de connaissances sur la multiplication. En effet, depuis le cycle primaire, ils explorent des concepts reliés à la multiplication à l’aide de matériel concret, de la calculatrice, d’illustrations et de symboles. En 4e année, la multiplication de fractions est limitée à la multiplication d’un nombre naturel par une fraction unitaire. Ce type de multiplication peut être compris en le reliant à l’addition répétée. Ainsi, les élèves saisissent facilement que \(3\; \times \;\frac{1}{2}\), qu’on peut lire « 3 fois un demi », est une multiplication qui peut être représentée par l’addition répétée, soit \(\frac{1}{2}\; + \;\frac{1}{2}\; + \;\frac{1}{2}\). Elles doivent être explorées pour aider les élèves à comprendre la multiplication des fractions.
Dans cette vidéo, deux élèves présentent comment ils ont effectué la multiplication d’un nombre naturel par une fraction propre à l’aide de l’addition répétée.
 Description de la vidéo
Description de la vidéo
Description à venir
Cependant, il est plus difficile de donner un sens à la multiplication d’une fraction à un nombre naturel (par exemple, \(\frac{1}{2}\; \times \;3\)). Ces situations sont explorées à partir de la 5e année. Il existe un lien entre le concept de multiplication par une fraction et celui de fraction d’un ensemble. La fraction d’un ensemble est un concept relié au concept de fraction. Par exemple, en 2e année, les élèves apprennent le sens de \(\frac{1}{2}\), \(\frac{1}{4}\) et \(\frac{1}{3}\) d’un groupe jusqu'à 10 objets. Plus tard, ils consolident leur compréhension du concept de fraction d’un ensemble en l’appliquant à d’autres fractions. En 6e année, en examinant le concept de multiplication d’un nombre naturel par une fraction propre, ils apprendront que la fraction d’un ensemble (\(\frac{2}{3}\) de 6) est reliée à la multiplication et que cette situation peut être représentée par une multiplication (\(\frac{2}{3}\; \times \;6\)). Il faut un bon degré d’abstraction pour accepter qu’une situation comme \(\frac{1}{2}\) de 12 soit considérée comme une multiplication.
Les mathématiciens et les mathématiciennes ont décidé qu’il s’agissait d’une multiplication en procédant à peu près comme suit :
- on peut considérer \(4\; \times \;6\) comme 4 groupes de 6;
- on peut considérer \(2\; \times \;8\) comme 2 groupes de 8.
On ne rencontre aucune difficulté à étendre ce constat à des nombres fractionnaires supérieurs à 2 :
- on peut considérer \(4\frac{1}{2}\; \times \;6\) comme 4 groupes et demi de 6;
- on peut considérer \(2\frac{1}{3}\; \times \;12\) comme 2 groupes et un tiers de 12.
On généralise cette situation (ce qui implique une abstraction, puisque le groupe n’est pas « multiplié » comme tel) en ajoutant que :
- on veut considérer \(1\frac{1}{2}\; \times \;6\) comme un groupe et demi de 6;
- on veut considérer \(\frac{1}{2}\; \times \;6\) comme un demi-groupe de 6.
Ainsi, c’est à la suite d’une interprétation de l’opération que \(\frac{1}{2}\) de 6 est considéré comme une multiplication de \(\frac{1}{2}\) et de 6.
Exemple
Dans une salle de classe de 6e année, \(\frac{1}{2}\) des élèves portent une tuque. S’il y a 24 élèves dans la salle de classe, combien d’élèves portent une tuque?
Source : adapté de Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 6e année, Module 2, Série 2, p. 281.
- Multiplication effectuée à l’aide d’une droite numérique double
Pour trouver \(\frac{1}{2}\) de 24, je divise 24 par 2, ce qui me donne 12.
Je représente les 24 élèves sous la droite et la moitié de 24 sur le haut de la droite.
 Image Une droite numérique est graduée de zéro à 26 par marques d’intervalles de deux. Au-dessus, une flèche relie zéro à douze en indiquant « douze élèves », et en dessous, une flèche relie zéro à 24 en indiquant « 24 élèves ».
Image Une droite numérique est graduée de zéro à 26 par marques d’intervalles de deux. Au-dessus, une flèche relie zéro à douze en indiquant « douze élèves », et en dessous, une flèche relie zéro à 24 en indiquant « 24 élèves ».
Il y a 12 élèves qui portent une tuque.
- Multiplication effectuée à l’aide de la disposition rectangulaire
Je décompose 24 en \(20\; + \;4\). Je détermine la moitié de 20 et la moitié de 4, \(10\; + \;2\; = \;12\).
 Image Un rectangle est traversé par une ligne verticale entre le centre et l’extrême droit. Au-dessus du rectangle, il est écrit le nombre 20 à gauche de la ligne verticale, et le chiffre quatre à droite de la ligne verticale. À l’intérieur du rectangle, il est écrit dix à gauche de la ligne verticale et deux à droite de la ligne. À gauche du rectangle, il est écrit un demi.
Image Un rectangle est traversé par une ligne verticale entre le centre et l’extrême droit. Au-dessus du rectangle, il est écrit le nombre 20 à gauche de la ligne verticale, et le chiffre quatre à droite de la ligne verticale. À l’intérieur du rectangle, il est écrit dix à gauche de la ligne verticale et deux à droite de la ligne. À gauche du rectangle, il est écrit un demi.
\(10\; + \;2\; = \;12\)
Il y a 12 élèves qui portent une tuque.
En 6e année, en s’attardant aux concepts et à une mise en contexte, il est plus pertinent d’approfondir le sens de la fraction d’un ensemble en effectuant un calcul (par exemple, \(\frac{2}{3}\) de 9) que de s’orienter vers la multiplication d’un nombre naturel par une fraction (\(\frac{2}{3}\; \times \;9\)).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 78-79.
Exemple
Dans un champ de forme rectangulaire dont l’aire est de 100 m2, M. Longpré a semé des concombres sur \(\frac{2}{5}\) de cette surface. Quelle est l’aire du champ, en m2, consacrée à la culture des concombres?
Source : adapté de Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 6e année, Module 2, Série 2, p. 309.
- Multiplication effectuée à l’aide de la disposition rectangulaire
J’ai décomposé 100 en \(25\; + \;25\; + \;25\; + \;25\). J’ai aussi décomposé \(\frac{2}{5}\) en \(\frac{1}{5}\; + \;\frac{1}{5}\). Je sais que \(\frac{1}{5}\) de 25 est 5 puisque \(5\; \times \;5\; = \;25\).
J’ai additionné les produits partiels pour arriver à 40.
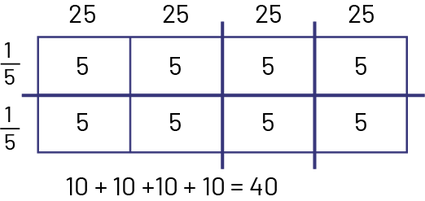 Image Un rectangle est divisé en huit parts égales, soit deux rangées de quatre parts, lesquelles possèdent chacune le chiffre cinq. Au-dessus de chaque colonne il est écrit 25, et à gauche de chaque rangée, il est écrit un cinquième. Sous le rectangle, il est écrit : dix plus dix plus dix plus dix égale 40.
Image Un rectangle est divisé en huit parts égales, soit deux rangées de quatre parts, lesquelles possèdent chacune le chiffre cinq. Au-dessus de chaque colonne il est écrit 25, et à gauche de chaque rangée, il est écrit un cinquième. Sous le rectangle, il est écrit : dix plus dix plus dix plus dix égale 40.
L’aire du champ consacrée à la culture des concombres est 40 m2.
- Multiplication effectuée à l’aide d’un algorithme personnel
J’ai décomposé \(\frac{2}{5}\) en \(2 \times \frac{1}{5}\).
À l’aide de l’associativité, j’ai multiplié \(\frac{1}{5}\; \times \;2\; \times \;100\).
J’ai multiplié \(\frac{1}{5}\; \times \;200\).
Multiplier par \(\frac{1}{5}\) est la même chose que diviser par 5.
J’obtiens 40.
\(\begin{align}\frac{2}{5}\; \times \;100\; = \;2\; \times \;\frac{1}{5}\; \times \;100\; &= \;\frac{1}{5}\; \times \;2\; \times \;100\\ &= \;\frac{1}{5}\; \times \;200\\ &= \;200\; \div \;5\\ &= \;40\end{align}\)
L’aire du champ consacrée à la culture des concombres est 40 m2.
Connaissance : fraction propre
Fraction dont le numérateur est plus petit que le dénominateur.
Exemples
\(\frac{2}{3}\), \(\frac{{11}}{{15}}\), \(\frac{{53}}{{123}}\)
