B2.9 Multiply whole numbers by proper fractions, using appropriate tools and strategies.
Multiplying Whole Numbers by Proper Fractions, Using Appropriate Tools and Strategies
In the junior grades, students have a background of knowledge about multiplication. Since the primary grades, they have been exploring concepts related to multiplication using concrete materials, the calculator, visual representations and symbols. In Grade 6, as they examine multiplying a whole number by a proper fraction, students will learn that the fraction of a set (for example, \(\frac{2}{3}\) of 6) is related to multiplication and that this situation can be represented by the expression \(\frac{2}{3}\; \times \;6\). It requires a good degree of abstraction to recognize that a situation like \(\frac{1}{2}\) of 12 is considered a multiplication. Similarly:
- we can consider \(4\; \times \;6\) as 4 groups of 6;
- we can consider \(2\; \times \;8\) as 2 groups of 8.
There is no difficulty in extending this observation to fractional numbers greater than 2:
- we can consider \(4 \frac{1}{2}\; \times \;6\) as 4 and one half groups of 6;
- we can consider \(2 \frac{1}{3}\; \times \;12\) as 2 and one third of 12.
- we can consider \(1\frac{1}{2} \times \;6\) as one and a half groups of 6;
- we can consider \(\frac{1}{2} \times \;6\) as a half group of 6.
Example
In a Grade 6 classroom, \(\frac{1}{2}\) of the students are wearing hats. If there are 24 students in the classroom, how many students are wearing a hat?
Source: Adapted and translated from Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 6e, Module 2, Série 2, p. 281.
- Multiplication using a double number line
To determine \(\frac{1}{2}\) of 24, I can use the inverse operation and divide 24 by 2, to find the halfway point on the line, which is 12.
I represented the 24 students below the line and half of them on top of the line.

There are 12 students wearing hats.
- Multiplication performed using an area model
I decomposed 24 into 20 and 4. I found half of 20 and half of 4, \(10\; + \;2\; = \;12\).

\(10\; + \;2\; = \;12\)
There are 12 students wearing hats.
In Grade 6, with a focus on concepts and contextualization, it is more relevant to deepen the meaning of a fraction of a set by performing a calculation (for example, \(\frac{2}{3}\) of 9) than to move toward symbolically multiplying a whole number by a fraction, such as \(\frac{2}{3}; \times \;9\).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p 78-79.
Example
In a rectangular field with an area of 100 m2, Mr. Siby has planted cucumbers on \(\frac{2}{5}\)of the field . What area of the field, in m2, is devoted to cucumbers?
Source: Adapted an translated from Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 6e, Module 2, Série 2, p. 309.
- Multiplication performed using an area model
I have decomposed 100 into \(25\; + \;25\; + \;25\; + \;25\). I also decomposed \(\frac{2}{5}\) into \(\frac{1}{5}\; + \;\frac{1}{5}\). I know that \(\frac{1}{5}\) of 25 is 5 since \(5\; \times \;5\; = \;25\).
I added up the partial products to arrive at 40.
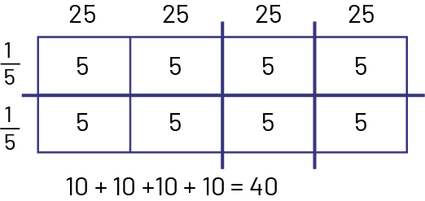
The area of the field dedicated to the cultivation of cucumbers is 40 m2.
- Multiplication Using a Personal Algorithm
I decomposed \(\frac{2}{5}\) into \(2\; \times \;\frac{1}{5}\).
Using the associative property, I multiplied \(\frac{1}{5}; \times \;2\; \times \;100\).
I multiplied \(\frac{1}{5}\; \times \;200\).
Multiplying by \(\frac{1}{5}\) is the same as dividing by 5.
I get 40.
\(\begin{align}\frac{2}{5}\; \times \;100\; = \;2\; \times \;\frac{1}{5}\; \times \;100\; &= \;\frac{1}{5}\; \times \;2\; \times \;100\\ &= \;\frac{1}{5}\; \times \;200\\ &= \;200\; \div \;5\\ &= \;40\end{align}\)
The area of the field dedicated to the cultivation of cucumbers is 40 m2.
Knowledge: Proper Fraction
Fraction whose numerator is less than the denominator.
Examples
\(\frac{2}{3}\), \(\frac{{11}}{{15}}\), \(\frac{{53}}{{123}}\)
